AIOps探索:基于VAE模型的周期性KPI异常检测方法——VAE异常检测
AIOps探索:基于VAE模型的周期性KPI异常检测方法
作者:林锦进
前言
在智能运维领域中,由于缺少异常样本,有监督方法的使用场景受限。因此,如何利用无监督方法对海量KPI进行异常检测是我们在智能运维领域探索的方向之一。最近学习了清华裴丹团队发表在WWW 2018会议上提出利用VAE模型进行周期性KPI无监督异常检测的论文:《Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in Web Applications 》[1](以下简称为Dount)。基于Dount论文的学习,本文将介绍如何使用Keras库,实现基于VAE模型的周期性KPI异常检测方法,包括其思路、原理与代码实现,帮助大家理解这个方法。
背景介绍:
在AI in All的时代,工业界中的运维领域提出了:智能运维(AIOps, Artificial Intelligence for IT Operations)这个概念,即采用机器学习、数据挖掘或深度学习等方法,来解决KPI异常检测、故障根因分析、容量预测等运维领域中的关键问题。
其中KPI异常检测是在运维领域中非常重要的一个环节。KPI(key performance indicators)指的是对服务、系统等运维对象的监控指标(如延迟、吞吐量等)。其存储的形式是按其发生的时间先后顺序排列而成的数列,也就是我们通常所说的时间序列。从运维的角度来看,存在多种不同类型的KPI,周期性KPI是其中一种典型的KPI,其特点表现为具有周期性,如下图:
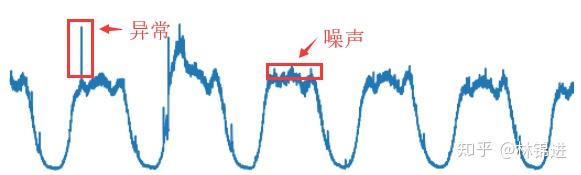
要进行KPI异常检测,首先我们要定义一下什么是异常。如上图所示,我们将KPI的异常点定义为超过期望值一定范围的点,而在期望值的小范围内波动的点我们将其认为是噪声。对周期性KPI的异常检测在工业界和学术界已有不少探索,本文将介绍基于深度学习模型VAE的无监督周期性KPI异常检测方法。
正文:
- AutoEncoder
因为VAE跟AutoEncoder在网络整体结构上相似,都分为Encoder和Decoder模型,那么在了解VAE之前,我们先了解什么是AutoEncoder模型。
AutoEncoder的意思是自编码器,这个模型主要由两个部分组成:encoder和decoder,可以把它理解为两个函数:z = encoder(x), x = decoder(z)。在AutoEncoder模型的思想中,我们期望能够利用encoder模型,将我们的输入X转换到一个对应的z,利用decoder模型,我们能够将z还原为原来的x,可以把AutoEncoder理解为有损的压缩与解压。
AutoEncoder模型有什么用呢?有两个主要功能:
- 降噪
- 将高纬的特征转为低纬度的特征(从X到z)。
要实现一个AutoEncoder其实非常简单(其实就是单个隐藏层的神经网络),有接触过深度学习的人应该都可以理解:
input = Input(shape=(seq_len,))
encoded = Dense(encoding_dim, activation='relu')(input)
decoded = Dense(seq_len)(encoded)
autoencoder = Model(input, decoded)
我们先来考虑一下能否用AutoEncoder进行KPI异常检测,以及它有什么缺点。因为AutoEncoder具有降噪的功能,那它理论上也有过滤异常点的能力,因此我们可以考虑是否可以用AutoEncoder对原始输入进行重构,将重构后的结果与原始输入进行对比,在某些点上相差特别大的话,我们可以认为原始输入在这个时间点上是一个异常点。
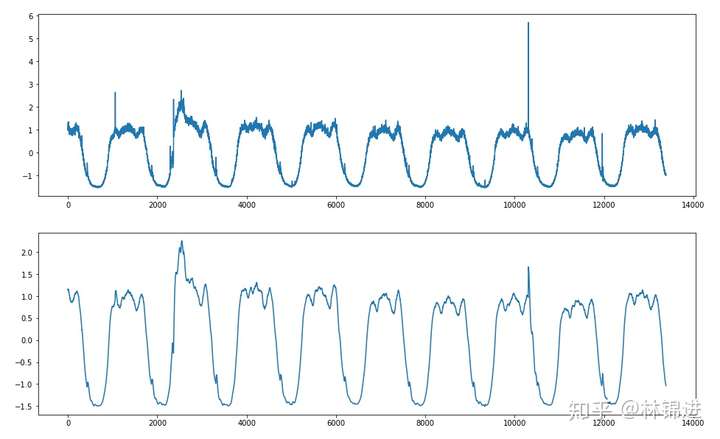
下面是一个简单的实验结果展示,我们训练了一个输入层X的维度设置为180(1分钟1个点,3小时数据),Z的维度设置为5(可以理解为原始输入降维后表达),输出成X的维度设置为180的AutoEncoder模型,并且测试集的数据进行重构(滑动窗口形式,每次重构后只记录最后一个点,然后窗口滑动到下一个时间点),能够得到以下结果:
- 基于AutoEncoder的周期性KPI异常检测:
上面提到,AutoEncoder具有降噪功能,那它怎么降噪呢?这里简单举一个例子:假设我们现在训练出来的模型可以得到这样的映射关系[1, 2](X)->[1](z)->[1 ,2]X_r, 其中[1, 2]表示二维向量, [1]表示一维向量,X_r表示重构后的X。这个例子表示了一个理想的AutoEncoder模型,它能将[1,2]降维到[1], 并且能从[1]重构为[1,2]。接下来,假设我们的输入为[1, 2.1],其中第二维度的0.1表示一个噪声,将其输入到encoder部分后得到的Z为[1],并且重构后得到的X_r是[1, 2], 这也就达到了一个对原始输入去噪的作用。
而我们的当前的目标是进行KPI异常检测,从上图可以看到,一些肉眼可见的异常在重构后被去除掉了(类似降噪了),通过对比与原始输入的差距,我们可以判断是否为异常。
然而,AutoEncoder模型本身没有什么多少正则化手段,容易过拟合,当训练数据存在较多异常点的时候,可能模型的效果就不会特别好,而我们要做的是无监督异常检测(要是有label的话就用有监督模型了),因此我们的场景是训练的时候允许数据存在少量异常值的,但当异常值占比较大的话,AutoEncoder可能会过拟合(学习到异常模式)。
- Variational AutoEncoder(VAE)
接下来介绍一些VAE模型,如果不需要对VAE有比较清楚的了解,也可以直接跳过这部分内容。
对于VAE模型的基本思想,下面内容主要引用自我觉得讲得比较清楚的一篇知乎文章,并根据我的理解将文中一些地方进行修改,保留核心部分,这里假设读者知道判别模型与生成模型的相关概念。
原文地址:https://zhuanlan.zhihu.com/p/27865705
VAE 跟传统 AutoEncoder关系并不大,只是思想及架构上也有 Encoder 和 Decoder 两个结构而已。VAE 理论涉及到的主要背景知识包括:隐变量(Latent Variable Models)、变分推理(Variational Inference)、Reparameterization Trick 等等。
首先,先定义问题:我们希望学习出一个生成模型,能产生训练样本中没有,但与训练集相似的数据。换一种说法,对于样本空间 ,当以
抽取数据时,我们希望以较高概率抽取到与训练样本近似的数据。对于手写数字的场景,则表现为生成像手写数字的图像。对于数据
的产生,我们假设它受一些隐含因素的影响,即隐变量(Latent Variables),写作
,并且假设
服从标准正态分布
。则原来对
建模转为对
进行建模,同时有
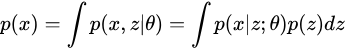
接下来我们可以开始解决最大化 的问题,如果我们知道
的分布,我们就可以利用采样来计算积分,即
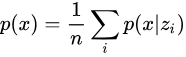
我们发现,当 时,对估计
没有帮助,所以其实我们只需要采样那些对
有贡献的
。此时,可以反过来求
,然而,
是intractable的,VAE中利用Variational Inference,引入
分布来近似
。
最终,可以得到需要优化的目标 ELBO(Evidence Lower Bound),此处其定义为
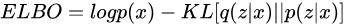
其中,第一项是我们希望最大化的目标;第二项是在数据
下真实分布
与假想分布
的距离,当
的选择合理时此项会接近为0。但公式中仍然含有intractable的
,于是将其化简后得到
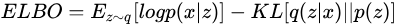
于是,对于某个样本 ,其损失函数可以表示为,每次输入为一个xi,
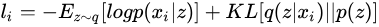
其中, 意味着在样本
下隐变量
的分布,对应于AutoEncoder中的Encoder部分;
意味着将隐变量
恢复成
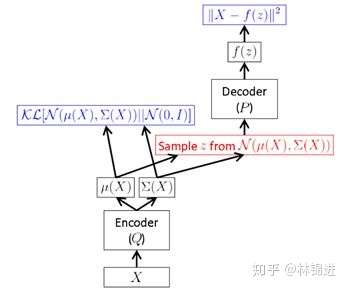
,对应着 Decoder。于是,VAE 的结构可以表示为
但是,上面这种方式需要在前向传播时进行采样,而这种采样操作是无法进行后向反馈梯度的。于是,作者提出一种“Reparameterization Trick”:将对采样的操作移到输入层进行。于是就有了下面的VAE最终形式
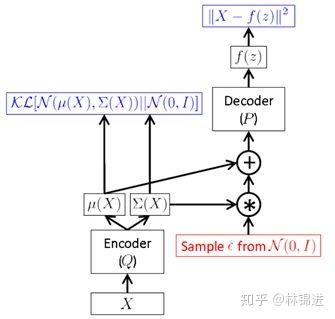
采样时,先对输入的进行采样,然后计算
,间接对
采样。
我们再结合两个图梳理一下VAE的过程。
下图表示了VAE整个过程。即首先通过Encoder 得到 的隐变量分布参数;然后采样得到隐变量
。接下来按公式,应该是利用 Decoder 求得
的分布参数,而实际中一般就直接利用隐变量恢复
。

下图展示了一个具有3个隐变量的 VAE 结构示意图。
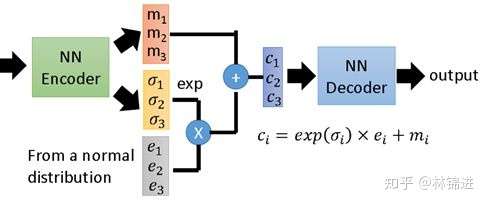
- 基于VAE的周期性KPI异常检测
上面介绍了VAE的原理,看起来很复杂,其实最终VAE也实现了跟AutoEncoder类似的作用,输入一个序列,得到一个隐变量(从隐变量的分布中采样得到),然后将隐变量重构成原始输入。不同的是,VAE学习到的是隐变量的分布(允许隐变量存在一定的噪声和随机性),因此可以具有类似正则化防止过拟合的作用。
以下的构建一个VAE模型的keras代码,修改自keras的example代码,具体参数参考了Dount论文:
def sampling(args):
"""Reparameterization trick by sampling fr an isotropic unit Gaussian.
# Arguments:
args (tensor): mean and log of variance of Q(z|X)
# Returns:
z (tensor): sampled latent vector
"""
z_mean, z_log_var = args
batch = K.shape(z_mean)[0]
dim = K.int_shape(z_mean)[1]
# by default, random_normal has mean=0 and std=1.0
epsilon = K.random_normal(shape=(batch, dim))
std_epsilon = 1e-4
return z_mean + (z_log_var + std_epsilon) * epsilon
input_shape = (seq_len,)
intermediate_dim = 100
latent_dim = latent_dim
# VAE model = encoder + decoder
# build encoder model
inputs = Input(shape=input_shape, name='encoder_input')
x = Dense(intermediate_dim, activation='relu', kernel_regularizer=regularizers.l2(0.001))(inputs)
x = Dense(intermediate_dim, activation='relu', kernel_regularizer=regularizers.l2(0.001))(x)
z_mean = Dense(latent_dim, name='z_mean')(x)
z_log_var = Dense(latent_dim, name='z_log_var', activation='softplus')(x)
# use reparameterization trick to push the sampling out as input
# note that "output_shape" isn't necessary with the TensorFlow backend
z = Lambda(sampling, output_shape=(latent_dim,), name='z')([z_mean, z_log_var])
# build decoder model
x = Dense(intermediate_dim, activation='relu', kernel_regularizer=regularizers.l2(0.001))(z)
x = Dense(intermediate_dim, activation='relu', kernel_regularizer=regularizers.l2(0.001))(x)
x_mean = Dense(seq_len, name='x_mean')(x)
x_log_var = Dense(seq_len, name='x_log_var', activation='softplus')(x)
outputs = Lambda(sampling, output_shape=(seq_len,), name='x')([x_mean, x_log_var])
vae = Model(inputs, outputs, name='vae_mlp')
# add loss
reconstruction_loss = mean_squared_error(inputs, outputs)
reconstruction_loss *= seq_len
kl_loss = 1 + z_log_var - K.square(z_mean) - K.exp(z_log_var)
kl_loss = K.sum(kl_loss, axis=-1)
kl_loss *= -0.5
vae_loss = K.mean(reconstruction_loss + kl_loss)
vae.add_loss(vae_loss)
vae.compile(optimizer='adam')
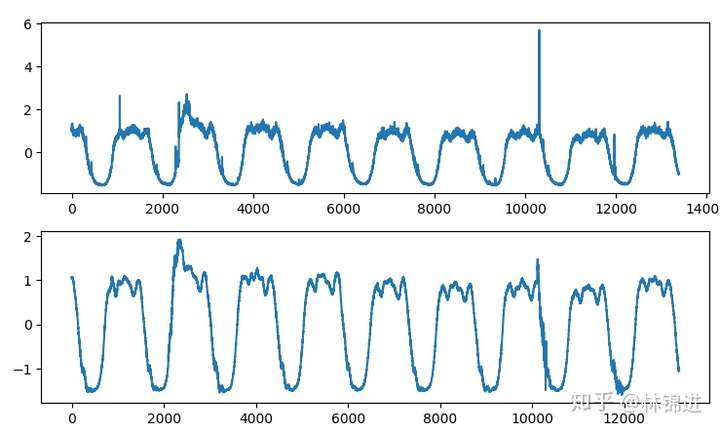
基于VAE的周期性KPI异常检测方法其实跟AutoEncoder基本一致,可以使用重构误差来判断异常,来下面是结果,上图是原始输入,下图是重构结果,我们能够看到VAE重构的结果比AutoEncoder的更好一些。
缺陷:
基于AutoEncoder和VAE模型在工业界上的使用面临的2个最大问题是:
- 理论上它只能对一个KPI训练单独一个模型,不同类型的KPI需要使用不同的模型,为了解决这个问题,裴丹团队后面又发表了一篇关于KPI聚类的论文《Robust and Rapid Clustering of KPIs for Large-Scale Anomaly Detection》,先对不同的KPI进行模板提取,然后进行聚类,对每个类训练单独一个模型。
- 需要设置异常阈值。因为我们检测异常是通过对比重构后的结果与原始输入的差距,而这个差距多少就算是异常需要人为定义,然而对于大量的不同类型的KPI,我们很难去统一设置阈值,这也是采用VAE模型比较大的一个缺陷。虽然在Dount论文中,采用的是重构概率而不是重构误差来判断异常,然而重构概率也需要设置阈值才能得到比较精确的结果。
总结
本文分别介绍了AutoEncoder和VAE模型以及基于这些模型的周期性KPI异常检测方法。裴丹的论文Dount中对原始的VAE做了一些改进,针对KPI异常检测这个场景增加了一些细节上的优化,如missing data injection、MCMC等等,这部分细节就不在本文中讨论了,有兴趣的同学可以看一下他们的开源代码 haowen-xu/donut。
最后,为了让对AIOps有兴趣的同学能够交流与学习,我创建了一个Awesome-AIOps的仓库,汇总一些AIOps相关的学习资料、算法/工具库等等,欢迎大家进行一起补充,互相进步。
如果文中有什么解释不清或者说错的地方,欢迎批评指正。
参考文献
[1] Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in Web Applications
[2] https://blog.keras.io/building-autoencoders-in-keras.html
[3] 当我们在谈论 Deep Learning:AutoEncoder 及其相关模型




 浙公网安备 33010602011771号
浙公网安备 33010602011771号