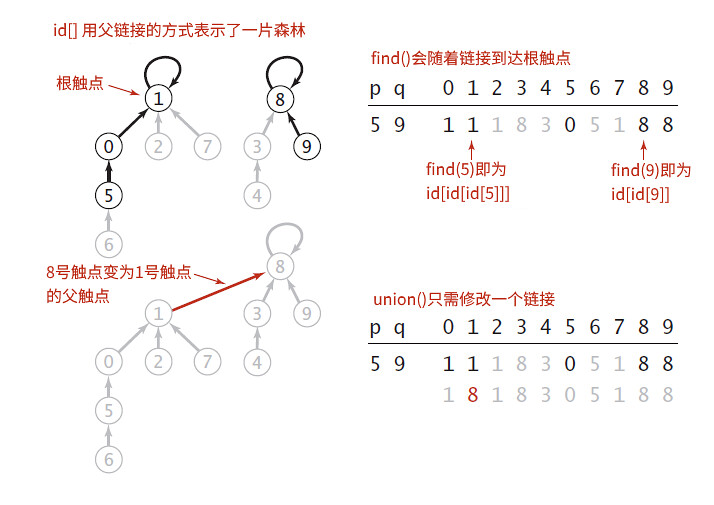
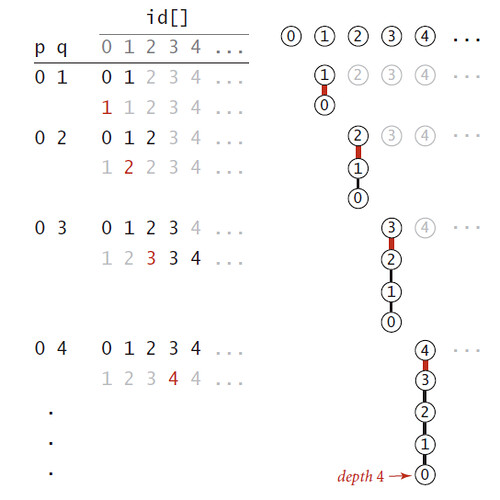
普林斯顿算法（1.3）并查集（union-find算法）——本质就是一个数 下面的子树代表了连在一起的点

转自：https://libhappy.com/2016/03/algs-1.3/

假设在互联网中有两台计算机需要互相通信，那么该怎么确定它们之间是否已经连接起来还是需要架设新的线路连接这两台计算机。这就是动态连通性问题。 动态连通性问题在日常生活中十分常见，比如上文所说的通信网络中的连通性问题，比如物理化学中的渗流问题。通过并查集这种数据结构及union-find 算法可以解决动态连通性问题。

动态连通性问题

概念

给出一系列的对象时，让其支持以下的两个操作：

• 判断两个对象是否相连
• 使两个对象相连

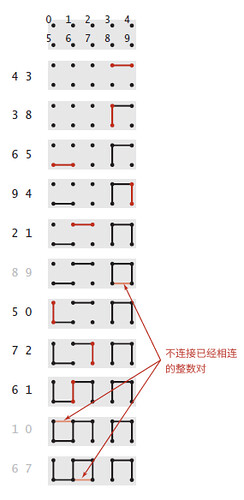
这里以整数代表对象，有0-9共十个整数，当给出一个整数对（a, b）时表示将整数a和b相连（如果a、b不相连）。如下图所示：

 

随着整数对的输入，十个整数的连通性会发生变化，这就是动态连通性问题。

在动态连通性问题中，我们假设“相连”是一种等价关系，也就意味着它具有：

• 自反性：p和p是相连的
• 对称性：如果p和q是相连的，那么q和p也是相连的
• 传递性：如果p和q是相连的且q和r是相连的，那么p和r是相连的。

在所有给出的对象中，所有相连的一组对象称为连通分量（Connected component）。如上图中最后一行的（0, 1, 2, 5, 6, 7）和（3, 4, 8, 9）分别为两个连通分量。

应用

• 计算机网络：判断网络中的计算机是否可以通过已存在的连接直接通信；
• 社交网络中的朋友关系：将朋友关系当作相连，判断两个人之间的朋友关系；
• 计算机芯片中晶体管的连接问题：判断芯片中晶体管是否相连；
• 变量名的等价性：某些编程语言（如FORTRAN）中允许声明两个等价的变量名，判断两个给定的变量名是否等价；
• 数学集合中的元素：元素可能属于不同的集合，将元素“相连”表示将两个元素所属的集合合并成一个集合。

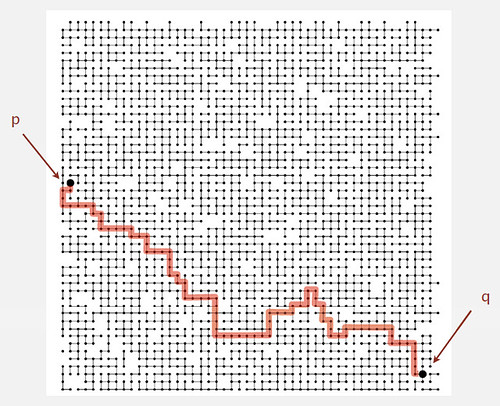
如在下图所示的所有连接中判断p和q点之间是否相连。

 

设计算法