机器学习算法原理实现——使用梯度下降求解线性回归

什么是梯度下降？

机器学习算法都需要最大化或最小化一个函数，这个函数被称为"目标函数"，其中我们一般把最小化的一类函数，称为"损失函数"。它能根据预测结果，衡量出模型预测能力的好坏。在求损失函数最小化的过程中使用梯度下降法。

$\frac{d J (θ)}{d θ}$

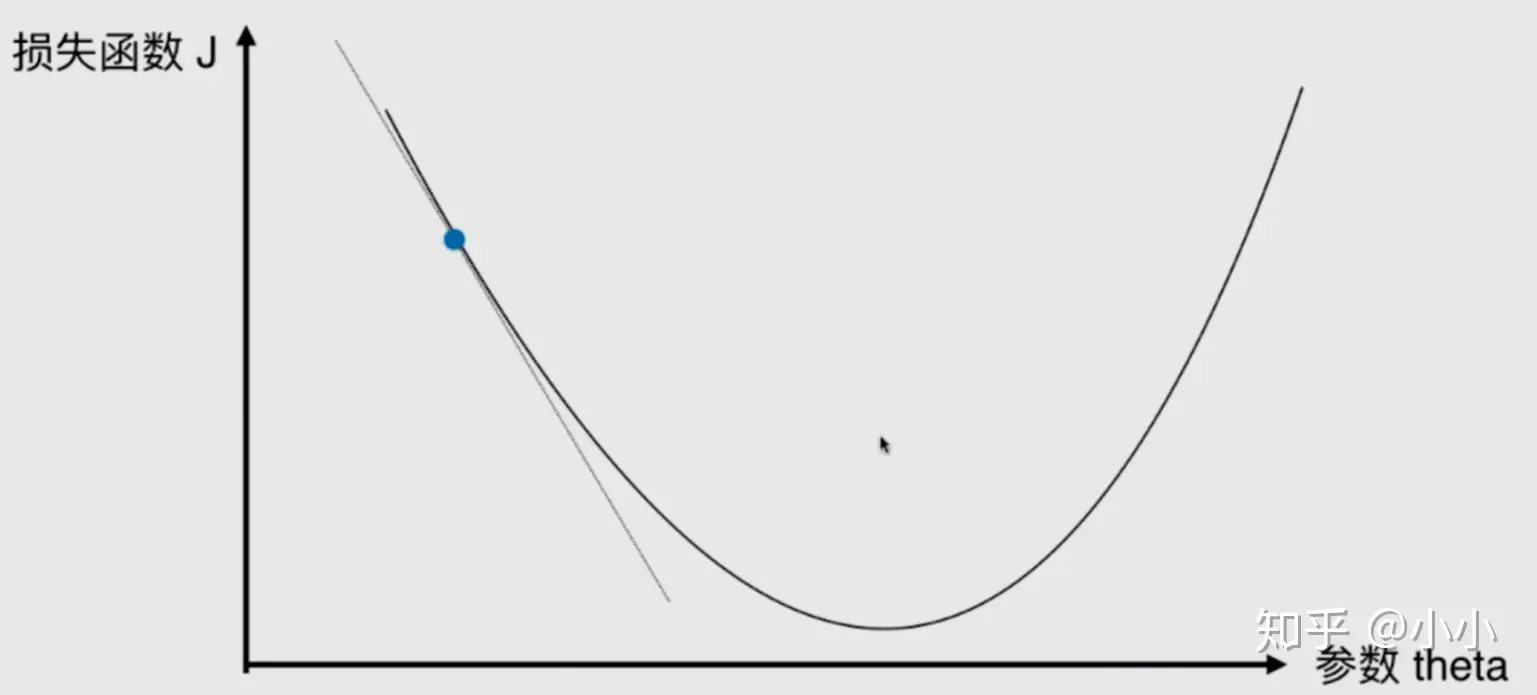
在直线方程中，导数代表斜率，在曲线方程中，导数代表切线的斜率。导数代表着参数 $θ$ 单位变化时，损失函数J相应的的变化。通过上面图中的点可以发现，该点的导数为负值，所以随着参数 $θ$ 的增加，损失函数J减小，因此导数从某种意义上还可以代表方向，对应着损失函数J增大的方向。

梯度下降法

对于梯度下降，我们可以形象地理解为一个人下山的过程。假设现在有一个人在山上，现在他想要走下山，但是他不知道山底在哪个方向，怎么办呢？显然我们可以想到的是，一定要沿着山高度下降的地方走，不然就不是下山而是上山了。山高度下降的方向有很多，选哪个方向呢？这个人比较有冒险精神，他选择最陡峭的方向，即山高度下降最快的方向。现在确定了方向，就要开始下山了。又有一个问题来了，在下山的过程中，最开始选定的方向并不总是高度下降最快的地方。这个人比较聪明，他每次都选定一段距离，每走一段距离之后，就重新确定当前所在位置的高度下降最快的地方。这样，这个人每次下山的方向都可以近似看作是每个距离段内高度下降最快的地方。现在我们将这个思想引入线性回归，在线性回归中，我们要找到参数矩阵使得损失函数最小。如果把损失函数看作是这座山，山底不就是损失函数最小的地方吗，那我们求解参数矩阵的过程，就是人走到山底的过程。

梯度下降的直观描述

$- η \frac{d J (θ)}{d θ}$

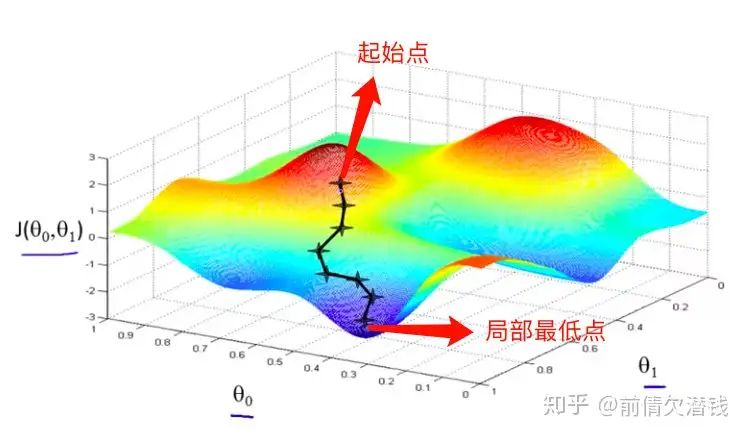
综上，如果最小化一个函数，我们就需要得到导数再取个负数，并且再乘以一个系数，这个系数通常叫做步长或者叫学习率(Learning rate, Lr)。 $η$ 的取值影响获得求最优解的速度，取值不合适的话甚至得不到最优解，它是梯度下降的一个超参数。 $η$ 太小，减慢收敛速度效率， $η$ 太大，甚至会导致不收敛。

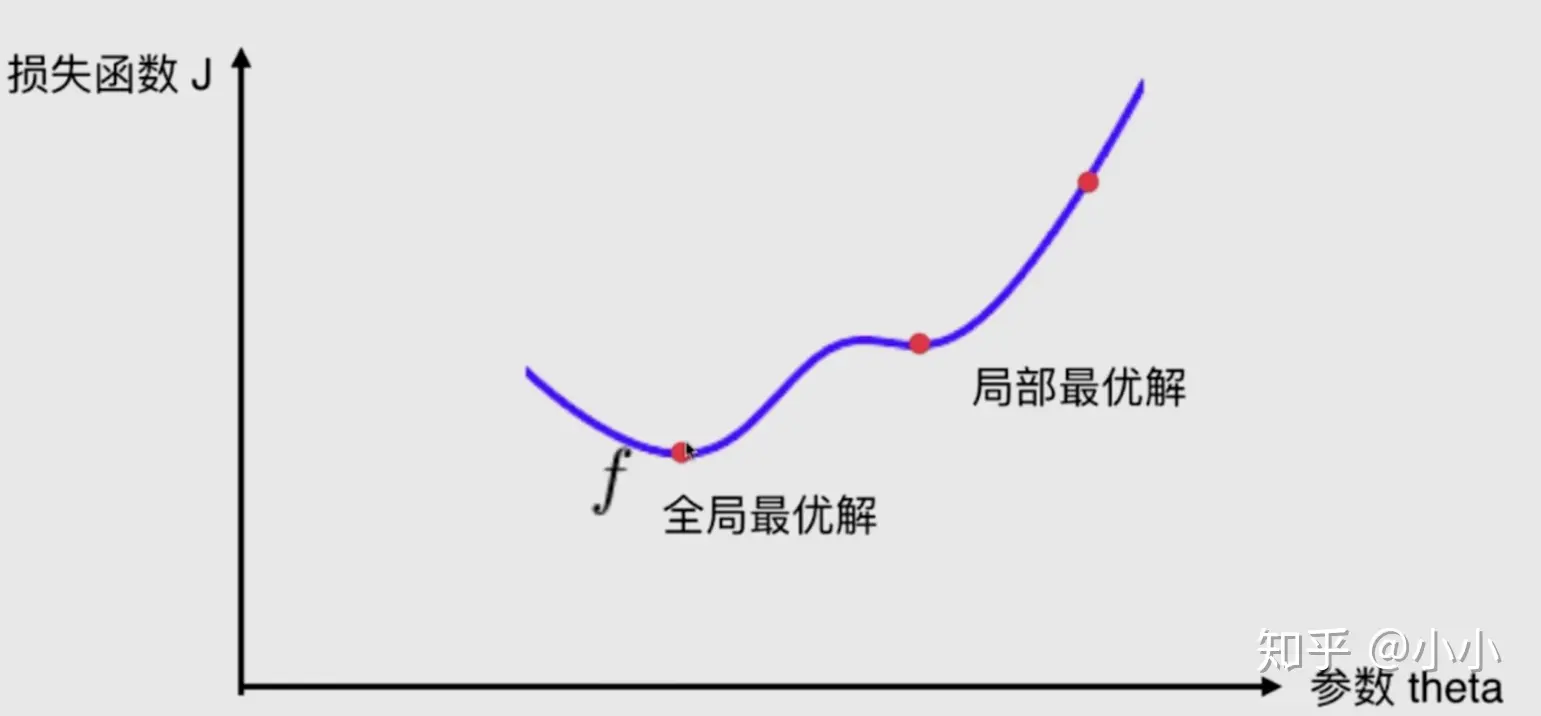
对于梯度下降算法而言，最不友好的就是并不是所有的函数都有唯一的极值点。很大概率就是局部最优解，并不是真正的全局最优解。这还只是针对二维平面来说，如果对于高维空间更加相对复杂的环境，就更不好说了。

解决方案：多次运行，随机化初始点。初始点也是梯度下降算法的一个超参数。初始化的方法也有很多。

模型表达(Model Representation)

以房屋交易问题为例，假使我们回归问题的训练集（Training Set）如下表所示：

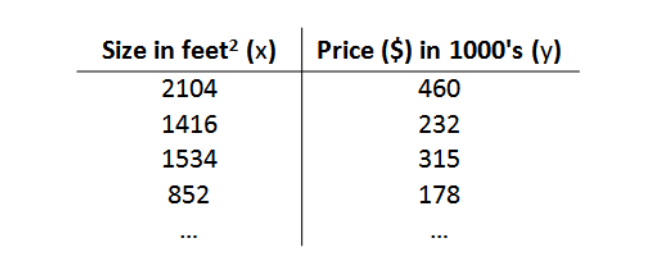
linear1

在该数据集中，只有一个自变量面积，和一个因变量价格，利用该数据集，我们的目的是训练一个线性方程，无限逼近所有数据点，然后利用该方程与给定的某一自变量（本例中为面积），可以预测因变量（本例中为房价）。我们将要用来描述这个回归问题的标记如下:

$m$ 代表训练集中实例的数量
$x$ 代表特征/输入变量
$y$ 代表目标变量/输出变量
$(x, y)$ 代表训练集中的实例
$(x^{(i)}, y^{(i)})$ 代表第 $i$ 个观察实例
$h$ 代表学习算法的解决方案或函数也称为假设

同时，分析得到的线性方程为：

$\begin{matrix} h_{θ} = θ_{0} + θ_{1} x \\ (1) \end{matrix}$

损失函数(Cost Function)

为了得到目标线性方程，我们只需确定公式中的 $θ_{0}$ 和 $θ_{1}$ ，为了确定所选定的 $θ_{0}$ 和 $θ_{1}$ 效果好坏，通常情况下，我们使用一个损失函数(Cost Function)或者说是错误函数(Error Function)来评估 $h_{θ}$ 函数的好坏。损失函数如下：

$\begin{matrix} \end{matrix}$

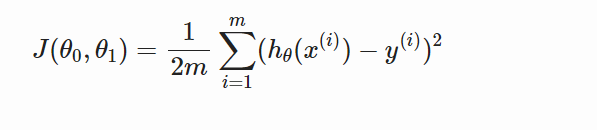
梯度下降(Gradient Descent)

梯度下降背后的思想是：开始时我们随机选择一个参数的组合 $(θ_{0}, θ_{1}, \dots, θ_{n})$ ，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值，因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否是全局最小值，不同的初始参数组合，可能会得到不同的局部最小值。

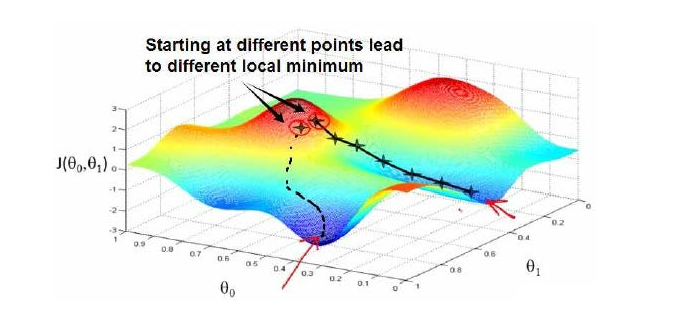
linear3

批量梯度下降(batch gradient descent)算法的公式为：

$\begin{matrix} \end{matrix}$

其中要求 $θ_{0}$ 和 $θ_{1}$ 同步更新。

好了，有了上面的理论，就可以开始写代码了：

自己写，不调用sklearn库（w，b对应theta1和theta0，实际的损失函数，从代码看，没有加2）：

import numpy as np


### 包括线性回归模型公式、均方损失函数和参数求偏导三部分
def linear_loss(X, y, w, b):
    '''
    输入：
    X：输入变量矩阵
    y：输出标签向量
    w：变量参数权重矩阵
    b：偏置
    输出：
    y_hat：线性回归模型预测值
    loss：均方损失
    dw：权重系数一阶偏导
    db：偏置一阶偏导
    '''
    # 训练样本量
    num_train = X.shape[0]
    # 训练特征数
    num_feature = X.shape[1]
    # print("num_train:", num_train, "num_feature:", num_feature)
    # 线性回归预测值
    y_hat = np.dot(X, w) + b
    # 计算预测值与实际标签之间的均方损失
    loss = np.sum((y_hat-y)**2) / num_train
    # 基于均方损失对权重系数的一阶梯度
    dw = np.dot(X.T, (y_hat-y)) / num_train
    # 基于均方损失对偏置的一阶梯度
    db = np.sum((y_hat-y)) / num_train
    return y_hat, loss, dw, db


### 初始化模型参数
def initialize_params(dims):
    '''
    输入：
    dims：训练数据的变量维度
    输出：
    w：初始化权重系数
    b：初始化偏置参数
    '''
    # 初始化权重系数为零向量
    w = np.zeros((dims, 1))
    # 初始化偏置参数为零
    b = 0
    return w, b


### 定义线性回归模型的训练过程
def linear_train(X, y, learning_rate=0.01, epochs=10000):
    '''
    输入：
    X：输入变量矩阵
    y：输出标签向量
    learning_rate：学习率
    epochs：训练迭代次数
    输出：
    loss_his：每次迭代的均方损失
    params：优化后的参数字典
    grads：优化后的参数梯度字典
    '''
    # 记录训练损失的空列表
    loss_his = []
    # 初始化模型参数
    w, b = initialize_params(X.shape[1])
    # 迭代训练
    for i in range(1, epochs):
        # 计算当前迭代的预测值、均方损失和梯度
        y_hat, loss, dw, db = linear_loss(X, y, w, b)
        # 基于梯度下降法的参数更新
        w += -learning_rate * dw
        b += -learning_rate * db
        # 记录当前迭代的损失
        loss_his.append(loss)
        # 每10000次迭代打印当前损失信息
        if i % 10000 == 0:
            print('epoch %d loss %f' % (i, loss))
        # 将当前迭代步优化后的参数保存到字典中
        params = {
            'w': w,
            'b': b
        }
        # 将当前迭代步的梯度保存到字典中
        grads = {
            'dw': dw,
            'db': db
        }
    return loss_his, params, grads


### 定义线性回归模型的预测函数
def predict(X, params):
    '''
    输入：
    X：测试集
    params：模型训练参数
    输出：
    y_pred：模型预测结果
    '''
    # 获取模型参数
    w = params['w']
    b = params['b']
    # 预测
    y_pred = np.dot(X, w) + b
    return y_pred


### 定义R2系数函数
def r2_score(y_test, y_pred):
    '''
    输入：
    y_test：测试集标签值
    y_pred：测试集预测值
    输出：
    r2：R2系数
    '''
    # 测试集标签均值
    y_avg = np.mean(y_test)
    # 总离差平方和
    ss_tot = np.sum((y_test - y_avg)**2)
    # 残差平方和
    ss_res = np.sum((y_test - y_pred)**2)
    # R2计算
    r2 = 1- (ss_res/ss_tot)
    return r2


from sklearn.datasets import load_diabetes
from sklearn.metrics import mean_squared_error, r2_score
# 导入打乱数据函数
from sklearn.utils import shuffle
# 获取diabetes数据集
print("hello linear regression!")
diabetes = load_diabetes()
# 获取输入和标签
data, target = diabetes.data, diabetes.target
# 打乱数据集
X, y = shuffle(data, target, random_state=13)
# 按照8∶2划分训练集和测试集
offset = int(X.shape[0] * 0.8)
# 训练集
X_train, y_train = X[:offset], y[:offset]
# 测试集
X_test, y_test = X[offset:], y[offset:]
print("sample data:")
print("X train:", X_train[:3, :])
print("y train:", y_train[:3])
print("y_train's shape(before): ", y_train.shape)
# 将训练集改为列向量的形式
"""
如果不转换，将会出错：
w += -learning_rate * dw
ValueError: non-broadcastable output operand with shape (10,1) doesn't match the broadcast shape (10,353)
"""
y_train = y_train.reshape((-1,1))
# 将测试集改为列向量的形式
y_test = y_test.reshape((-1,1))
# 打印训练集和测试集的维度
print("X_train's shape: ", X_train.shape)
print("X_test's shape: ", X_test.shape)
print("y_train's shape: ", y_train.shape)
print("y_test's shape: ", y_test.shape)

# 线性回归模型训练
loss_his, params, grads = linear_train(X_train, y_train, 0.01, 2000000)
# 打印训练后得到的模型参数
print(params)
# 基于测试集的预测
y_pred = predict(X_test, params)
# 计算测试集的R2系数
print(r2_score(y_test, y_pred))
print("Mean squared error: %.2f"% mean_squared_error(y_test, y_pred))

调用sklearn库：

# 导入线性回归模块
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score
# 定义模型实例
regr = linear_model.LinearRegression()
# 模型拟合训练数据
regr.fit(X_train, y_train)
# 模型预测值
y_pred = regr.predict(X_test)
# 输出模型均方误差
print("Mean squared error: %.2f"% mean_squared_error(y_test, y_pred))
# 计算R2系数
print('R Square score: %.2f' % r2_score(y_test, y_pred))

结果对比：

{'w': array([[ 9.54268206],
[-241.53370322],
[ 492.37500975],
[ 299.70559426],
[-265.83895789],
[ 28.52123883],
[ -89.79909026],
[ 227.71751438],
[ 484.58653273],
[ 50.50343372]]), 'b': 150.83964763327302}
0.5356698258124314 ==》上面自己写的
Mean squared error: 3397.78

Mean squared error: 3371.87
R Square score: 0.54 ==》调用sklearn的

可以看到二者基本上很接近了！

代码解释：

# 基于均方损失对权重系数的一阶梯度

dw = np.dot(X.T, (y_hat-y)) / num_train 为啥这样写？见下：

补充：为啥y要reshape，见下图即可知道：

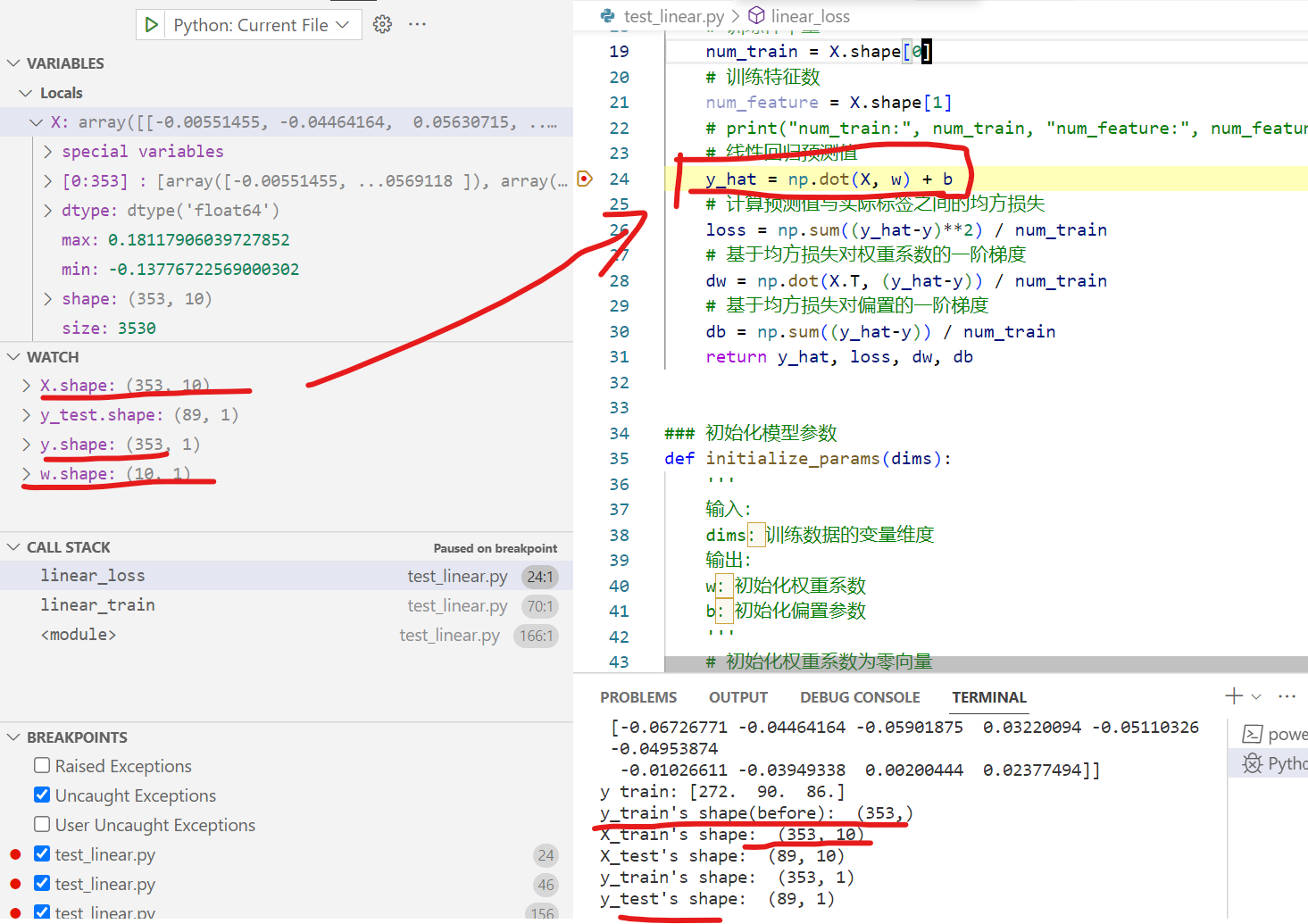
注意：

sklearn的LinearRegression模型使用的是均方误差（Mean Squared Error，MSE）作为损失函数。均方误差的公式如下：

MSE = 1/n * Σ(yi - ŷi)^2

其中，n是样本数量，yi是真实值，ŷi是预测值。LinearRegression模型通过最小化这个损失函数来学习最佳的参数。

posted @ 2023-09-06 19:58 bonelee 阅读(110) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

将者，智、信、仁、勇、严也。

Hi，我是李智华，华为-安全AI算法专家，欢迎来到安全攻防对抗的有趣世界。

机器学习算法原理实现——使用梯度下降求解线性回归

什么是梯度下降？

梯度下降法

模型表达(Model Representation)

$\begin{matrix} h_{θ} = θ_{0} + θ_{1} x \\ (1) \end{matrix}$

损失函数(Cost Function)

$\begin{matrix} \end{matrix}$

梯度下降(Gradient Descent)

$\begin{matrix} \end{matrix}$

好了，有了上面的理论，就可以开始写代码了：

公告

将者，智、信、仁、勇、严也。

Hi，我是李智华，华为-安全AI算法专家，欢迎来到安全攻防对抗的有趣世界。

机器学习算法原理实现——使用梯度下降求解线性回归

什么是梯度下降？

梯度下降法

模型表达(Model Representation)

hθ=θ0+θ1x(1)(1)ℎ�=�0+�1�

损失函数(Cost Function)

(2)�(�0,�1)=12�∑�=1�(ℎ�(�(�))−�(�))2

梯度下降(Gradient Descent)

(8)�1:=�1−�1�∑�=1�((ℎ�(�(�))−�(�))(�(�)))

好了，有了上面的理论，就可以开始写代码了：

公告

$\begin{matrix} h_{θ} = θ_{0} + θ_{1} x \\ (1) \end{matrix}$

$\begin{matrix} \end{matrix}$

$\begin{matrix} \end{matrix}$