Converting Boolean-Logic Decision Trees to Finite State Machines 如何将布尔表达式转换为有限状态机,用于更简单、高性能的网络安全事件检测
Converting Boolean-Logic Decision Trees to Finite State Machines
for simpler, high-performance detection of cybersecurity events
将布尔逻辑决策树转换为有限状态机
用于更简单、高性能的网络安全事件检测
When analyzing cybersecurity events, the detection algorithm evaluates attributes against boolean expressions to determine whether the event belongs to a class. This article describes converting boolean expressions to finite state machines to permit simpler, high-performance evaluation.
The open-source project Cyberprobe features this implementation. Conversion of rules to finite state machine (FSM) and application of the rules in FSM form is implemented in Python. Cyberprobe supports the use of millions of rules, which can be applied at greater than 200k events/second on a single processor core.
在分析网络安全事件时,检测算法会根据布尔表达式评估属性,以确定事件是否属于某个类别。本文描述了将布尔表达式转换为有限状态机以允许更简单、高性能的评估。
开源项目 Cyberprobe 以这种实现为特色。将规则转换为有限状态机 (FSM) 以及以 FSM 形式应用规则是在 Python 中实现的。Cyberprobe 支持使用数百万条规则,这些规则可以在单个处理器内核上以超过 20 万个事件/秒的速度应用。
Problem
Applying boolean logic criteria to events solves many scanning and detection problems. For instance, an event occurs that is generated from an interaction with a service under protection. The event has the following attributes:
- Source address:
123.123.123.123:14001 - Destination address:
192.168.0.1:19001 - URL:
https://myservice.com/path1
One or more boolean expressions for the class of thing I am trying to detect:
If TCP port number is 80 or 8080 AND IP address is 10.0.0.1 AND URL is http://www.example.com/malware.dat OR http://example.com/malware.dat …要检测的IDS/IPS表达式!
The aim is to analyze a high-rate stream of such events against a large set of boolean expressions to classify the events.
The boolean expressions get unreadable quickly with English, which has no built-in operator precedence.
Boolean expressions
Boolean operators are represented as functions, and type:value represents attribute type/value match terms.
and(
or(
tcp:80, tcp:8080
),
ipv4:10.0.0.1,
or(
url:http://www.example.com/malware.dat,
url:http://example.com/malware.dat
)
)
A boolean expression consists of a combination of, and(…), or(…) and not(…) functions, along with type:value match terms. I am using type:value pairs for match terms as that is useful in the domain I’m working in, but we could just as easily use strings.
Input
When evaluating the attributes of an event, attributes are type:value pairs. e.g. 输入长成酱紫!
ipv4:123.123.123.123
tcp:14001
ipv4:192.168.0.1
tcp:19001
url:https://myservice.com/path1
A basic evaluation algorithm
一个基本的评估算法
使用对输入评估布尔表达式的一种简单方法type:value是将布尔表达式表示为树,然后使用type:value对来触发评估。观察结果存储在树中。
A simple approach for evaluation of a boolean expression using type:value pair input is to represent the boolean expression as a tree, and then use type:value pairs to trigger evaluation. Observations are stored in the tree.

The rules for evaluating a boolean tree against an event are:
- For each
type:valueattribute, see if there is a correspondingtype:valueterm in the boolean tree. If it exists, set the term node as true, and evaluate the parent node. - When evaluating a parent or node, when any child is true, the or node is true, and its parent node is evaluated.
- When evaluating a parent and node, when ALL children are true, the and node is true, and its parent node is evaluated.
- When evaluating a parent not node, when the child node is true, the not node is false. Once evaluation of all attributes is complete, if a not node has not been deemed false because its child is false, then it is evaluated true, and it’s parent node is evaluated.
That’s a straightforward algorithm; the point of this article is to provide an optimization.
There is a compromise here, the algorithm to convert the boolean tree to an FSM is compute intensive: it has complexity which is non-linear with the number of nodes: it is linear with the product of combination nodes (described below) and type:value terms. In real-world scenarios, boolean expressions will be converted to FSM when the rule is parsed, thereafter the FSM can be used numerous times.
针对事件评估布尔树的规则是:==》其实思路很简单,就是自下而上去更新那个树,看能否求出root节点的值!
- 对于每个
type:value属性,查看布尔树中是否有对应type:value的项。如果存在,则将术语节点设置为真,并评估父节点。 - 在评估父节点或节点时,当任何子节点为真时,或节点为真,并评估其父节点。
- 在评估父节点和节点时,当所有子节点都为真时,节点为真,并评估其父节点。
- 在评估父非节点时,当子节点为真时,非节点为假。一旦完成所有属性的评估,如果非节点因为其子节点为假而未被视为假,则将其评估为真,并评估其父节点。
这是一个简单的算法;这篇文章的重点是提供一个优化。
这里有一个折衷,将布尔树转换为 FSM 的算法是计算密集型的:它的复杂性与节点数呈非线性关系:它与组合节点(如下所述)和type:value项的乘积呈线性关系。在现实场景中,布尔表达式会在解析规则时转换为 FSM,此后 FSM 可以被多次使用。
Converting to an FSM
Step 1: Identify the ‘basic states’
转换为 FSM
第 1 步:确定“基本状态”
In order to find the FSM, we look for all of the nodes in the boolean tree where state needs to be observed as evaluation proceeds. If you look at the example above, you can see that or nodes and and nodes are different. A child of an or node when evaluated as true immediately results in its parent being true, so no state needs to be kept regarding the children of or nodes. Whereas, when a child of an and node is true this is something which may need to be stored for later evaluation to determine the point at which the and node can be evaluated true. 为了找到 FSM,我们在布尔树中寻找所有需要在评估过程中观察状态的节点。如果您查看上面的示例,您会发现or节点和and节点是不同的。或节点的子节点在评估为真时立即导致其父节点为真,因此无需保留关于节点或节点的子节点的状态。然而,当and节点的子节点为真时,可能需要存储这些内容以供以后评估以确定and节点可以被评估为真的点。
The evaluation of not nodes is also complicated: a not node can be evaluated as true by virtue of its child maintaining a false evaluation for the duration of analysis.
The rules we state here are that some nodes in the boolean tree can be described as basic states:
- The root of a tree is inherently a
hitstate, which means the boolean expression is true. This is a basic state. - A not node is never a basic state.
- A child of an and node is a basic state unless it is a not node.
- A child of a not node is a basic state unless it is a not node itself.
布尔树中的一些节点可以描述为基本状态:
- 树的根本质上是一个
hit状态,这意味着布尔表达式为真。这是一个基本状态。 - 非节点永远不是基本状态。
- and节点的子节点是基本状态,除非它是 not节点。==》and也有布尔子表达式呢???
- 非节点的子节点是基本状态,除非它本身是非节点。
In the above example, the basic states are the two or nodes, and the ip:10.0.0.1 node. All qualify under rule 3.
The implementation gives each state a state name which consists of the letter s plus a unique number, assigned in a depth-first walk.该实现为每个状态提供了一个状态名称,该名称由字母s加上一个唯一的数字组成,在深度优先遍历中分配。 The example boolean tree with states is shown below; the three children of the and node are given states, with the parent and node representing the hit state.

Step 2: Identify the ‘combination states’
第 2 步:确定“组合状态”
The basic states are nodes where partial state needs to be recorded. One node in an FSM represents all state at the same time i.e. all the valid basic state combinations. Hence the combination states set consists all combinations of basic states. This includes the empty set, and a union of all states.组合状态集包含基本状态的所有组合。这包括空集和所有状态的并集。
Combination states need to have a state name: in my implementation, I combine states to a name by ordering, separating state numbers with a hyphen preceded by s. For example, a combination of states s4, s7, s13 is called s4–7-13.
The empty set has a special name which we call init. It represents the initial state of the FSM where no information is known. 组合状态需要有一个状态名称:在我的实现中,我通过排序将状态组合成一个名称,状态编号与前面的连字符分隔s。例如,状态s4、s7、的组合s13称为s4–7-13。
There is a special state hit which is used to describe any combination of basic states which include the root node evaluating to true. The combination of other states is ignored.
In the above example, the combination state set consists of:
init: The empty sets3: The first or node:s4: Theip:10.0.0.1nodes7: The second or nodes3-4: The first or node andip:10.0.0.1s4-7: Theip:10.0.0.1node and the second or nodes3-7: The first and second or nodeshit: the root node
空集有一个特殊的名字,我们称之为init。它表示 FSM 的初始状态,其中没有信息是已知的。
有一种特殊状态hit,用于描述基本状态的任意组合,其中包括评估为真的根节点。忽略其他状态的组合。
在上面的例子中,组合状态集包括:
init: 空集s3:第一个或节点:s4:ip:10.0.0.1节点s7:第二个或节点s3-4:第一个或节点和ip:10.0.0.1s4-7:ip:10.0.0.1节点和第二个或节点s3-7:第一和第二或节点hit:根节点
Step 3: Find all match terms
This is the set of all type:value match nodes in the boolean expression tree.
第 3 步:查找所有匹配项
这是type:value布尔表达式树中所有匹配节点的集合。
第 4 步:查找所有转换
Step 4: Find all transitions
This step is essentially about working out what all type:value match nodes do to all combination states. There is a special match term, end: which is used to evaluate what happens to not nodes when the list of terms is completed.
这一步本质上是关于计算出所有type:value匹配节点对所有组合状态的作用。有一个特殊的匹配项,end:用于评估项列表完成时非节点发生的情况。
The algorithm is:
For every combination state:
Work out the state name of that 'input' combination state
For every match term:
Given the input state
What state results from evaluating that term as true?
Work out the state name of that 'output' combination state
Record a transition (input, match term, output)
Given the input state
What state results from evaluating end: as true?
Work out the state name of that 'output' combination state
Record a transition (input, end:, output)
对于每个组合状态:
计算出该“输入”组合状态的状态名称
对于每个匹配项: ==》就是树的自下而上匹配!无非是变成了FSM。
给定输入状态
评估是否为真?是的话会产生什么状态?
计算出该“输出”组合状态的状态名称
记录一个转换(输入、匹配项、输出)
给定输入状态
评估 end:节点 的结果是什么状态:为真?
计算出该“输出”组合状态的状态名称
记录一个转换(输入,结束:,输出)
For this analysis, when the whole boolean expression evaluates as true i.e. the root node of the boolean expression is true, we give that a special name hit. 对于这个分析,当整个布尔表达式的计算结果为真时,即布尔表达式的根节点为真,我们给它一个特殊的名字hit。
The result is a complete set of triples: (input, term, output). If the input and output states are the same, we can ignore the transition so that the FSM only contains edges which change state.
At this point, the FSM has some inefficiencies: there may be areas of the FSM which it is not possible to navigate to from init. This is addressed in the next step.
Step 5: Remove invalid transitions
第 5 步:删除无效转换
并非所有组合状态都可以从 达到init,因此发现的一些转换可以作为无关紧要而丢弃。
Not all combination states can be reached from init, and so some of the transitions discovered can be discarded as irrelevant.
We start by constructing a set of states which can navigate to hit:
- Create a set containing only the combination state
hit. - Iterate over the FSM adding all transitions for which there is a navigation to any state in the set.
- Repeat 2. until the full set of states is discovered.
At this point we know all states which can lead to hit. However, there will be transitions which lead to states which are not in this set, and thus cannot ever travel to hit. So, the first simplification of invalid transitions is to reduce all transitions to states which are NOT in this set to the single state named fail.
There is a second simplification of the FSM: some of the states are not navigable from init, and can be removed:
- Construct a set containing only
init. - Iterate over the FSM finding all transitions for which there is a navigation from any state in the set.
- Repeat 2. until the set of states is discovered.
At this point we know areas of the FSM which are not reachable, and they can be removed.
Resultant FSM
结果 FSM
上述二叉树的 FSM 如下图所示。状态表示初始initFSM 状态。该hit状态表示布尔表达式成功评估为真。。。。。请参阅下面的示例。
The FSM of the above binary tree is depicted below. The init state represents the initial FSM state. The hit state represents successful evaluation of the boolean expression as true. We have mentioned the fail state, which only occurs when not expressions are used, which do not appear as a result of the boolean expression described as above. See below for an example.

Using the FSM
Evaluation of a boolean expressions using the FSM is simple:
- The FSM starts in the
initstate. - As attributes are discovered, the
type:valueis compared to the transitions from the current state. If a transition exists, the FSM moves to a new state. - When the
hitstate is achieved, that is the equivalent of the boolean expression evaluating to true. - When the
failstate is achieved, no further attribute discovery is needed, and the evaluation can be fast-failed.
The fact that for each term a single FSM lookup is needed means that this approach has performance advantages.
使用有限状态机
使用 FSM 计算布尔表达式很简单:
- FSM 在该
init状态下启动。 - 当发现属性时,会将其
type:value与当前状态的转换进行比较。如果存在转换,则 FSM 会移动到新状态。 - 当达到
hit状态时,这相当于布尔表达式的计算结果为真。 - 当达到
fail状态时,不需要进一步的属性发现,并且评估可以快速失败。
事实上,对于每个项都需要一个 FSM 查找,这意味着这种方法具有性能优势。
Example 2: Using not
For this example, the not node is used:
and(
not(
or(
tcp:8081, tcp:8082
)
),
and(
tcp:80,
or(
url:http://www.example.com/malware.dat,
url:http://example.com/malware.dat
)
)
)

It is interesting to view this graph before removal of invalid transitions and discovery of fail states. Some example artifacts:
- There is no transition to the combination state consisting only of state
s9. This is because it is not possible to arrive at this state without evaluating boths5ands8as true. There are transitions that lead froms9, to hit, but there is no path which leads to thes9state, so they can never be taken. - State
s5-8is similarly not valid, ifs5ands8are evaluated as true,s9is also true. In both cases, the valid state for this condition would bes5-8-9. This results in an unreachable part of the FSM with two nodes which is not connected with the rest of the FSM. - Any state with
s3true cannot lead tohitbecause the root and node is necessarily false. All nodes which includes3can be replaced by thefailstate.

After removal of invalid transitions and mapping to fail states, the FSM is easier to understand:

This example illustrates the fail state: once transitions lead to this state, it is not possible for further information to permit transition to the hit state. Discovering tcp:8081 or tcp:8082 to be present in any state causes a transition to the fail state. The fail state could be useful depending on your analysis strategy: it may be a point to fast-fail and shortcut further evaluation. This example also illustrates the special end: term which leads to hit.
这个例子说明了fail状态:一旦转换导致这个状态,就不可能有更多的信息允许转换到这个hit状态。发现tcp:8081或tcp:8082处于任何状态都会导致向该fail状态的转换。根据您的分析策略,失败状态可能有用:它可能是快速失败和进一步评估的捷径。此示例还说明了end:导致 的特殊项hit。
Example 3: More state
This example requires much more state to be kept as a result of all of the and conditions.
and(
or(
url:http://www.example.com/malware.dat,
url:http://example.com/malware.dat
),
ipv4:10.0.0.1,
not(
and(
or(
tcp:8081,
tcp:8082
),
ipv4:10.0.0.2
)
)
)

The resultant FSM has many states as a result:

Evaluating many rules concurrently
The FSM model lends itself to highly performant scanning using a large set of rules, each converted to an FSM using the approach described above. While it is theoretically possible to produce an uber-FSM from the individual FSMs, the size of the FSM rapidly becomes unwieldly. As there needs to be a single state in the uber-FSM for each combination of states in the set of contributary FSMs.
However, tracking a large number of FSM states concurrently could be compute-intensive.
A simple evaluation approach is to identify a set of initiators, which are the set of terms which lead away from the init state in each FSM. If any of the initiators are detected while analyzing attributes, the corresponding FSM is activated and put on the set of FSMs which are being tracked for state changes in subsequent match term evaluation. This approach reduces the number of FSMs which need to be tracked. I find in practice, this results in a small set of FSMs used for evaluation.
Using this approach, it is not appropriate to fast-fail an FSM and remove it from the set of tracked FSMs; FSMs must be tracked to the fail state, to prevent the FSM from subsequently being re-activated.
同时评估许多规则
FSM 模型适用于使用大量规则进行高性能扫描,每个规则都使用上述方法转换为 FSM。虽然理论上可以从单个 FSM 生成 uber-FSM,但 FSM 的大小很快就会变得笨重。因为在 uber-FSM 中,对于贡献 FSM 集合中的每个状态组合,都需要有一个单一的状态。
然而,同时跟踪大量 FSM 状态可能是计算密集型的。
一种简单的评估方法是确定一组启动器,这是一组远离init每个 FSM 中的状态的术语。如果在分析属性时检测到任何发起者,则相应的 FSM 将被激活并放置在 FSM 集合中,这些 FSM 在随后的匹配项评估中被跟踪状态变化。这种方法减少了需要跟踪的 FSM 的数量。我在实践中发现,这会产生一小组用于评估的 FSM。
使用这种方法,使 FSM 快速失败并将其从跟踪的 FSM 集中删除是不合适的;必须跟踪 FSM 到故障状态,以防止 FSM 随后被重新激活。
Implementation: cyberprobe indicators
cyberprobe项目包括一种以JSON 格式编写规则的方法。有许多实用程序可以解析规则格式并输出 FSM 信息,例如获取规则/指标文件并转储文件中每个规则的 FSM。这是以人类可读形式显示状态转换的输出:indicators-show-fsm(todo,实践下)
The cyberprobe project includes a means to write rules in JSON format. There are a number of utilities which parse the rule format and output FSM information e.g. indicators-show-fsm takes a rule/indicator file and dumps out the FSMs of every rule in the file. This is output in human-readable form showing the state transitions:
[indicators]$ indicators-show-fsm case1.json
3ce77704-abe4–4527–84e6-ed6a745aebcf: URL of a page serving malware
init — tcp:8080 -> s6
init — tcp:80 -> s6
init — url:http://example.org/malware.dat -> s3
init — url:http://www.example.org/malware.dat -> s3
s3 — tcp:8080 -> hit
s3 — tcp:80 -> hit
s6 — url:http://example.org/malware.dat -> hit
s6 — url:http://www.example.org/malware.dat -> hit
indicators-graph-fsm is a utility which takes a rule/indicator file and a rule ID, and outputs a Graphviz format graph describing the FSM, which is how I generated the diagrams in this article:
indicators-graph-fsm是一个实用程序,它采用规则/指标文件和规则 ID,并输出描述 FSM 的 Graphviz 格式图形,这就是我在本文中生成图表的方式:
[indicators]$ indicators-graph-fsm case1.json \
3ce77704-abe4–4527–84e6-ed6a745aebcf > graph.dot
[indicators]$ dot -Tpng graph.dot > graph.png
indicators-dump-fsm is a utility which takes an indicator file and outputs the FSM in a JSON form.
You can embed the FSM transformation in your code using the cyberprobe.fsm_extract module:
cyberprobe.fsm_extract您可以使用以下模块将 FSM 转换嵌入代码中:==》状态机就这个了吧!根据这个输出的状态转换表就可以用来写代码了!!!todo,实践下!
#!/usr/bin/env python3import sys
import cyberprobe.fsm_extract as fsme
from cyberprobe.logictree import And, Or, Not, Matchexpression = And([
Or([
Match("tcp", "80"), Match("tcp", "8080")
]),
Match("ipv4", "10.0.0.1"),
Or([
Match("url", "http://www.example.com/malware.dat"),
Match("url", "http:/example.com/malware.dat")
])
])fsm = fsme.extract(expression)# Dump out FSM
for v in fsm:
for w in v[1]:
print(" %s -- %s:%s -> %s" % (v[0], w[0], w[1], v[2]))
A quick word on performance
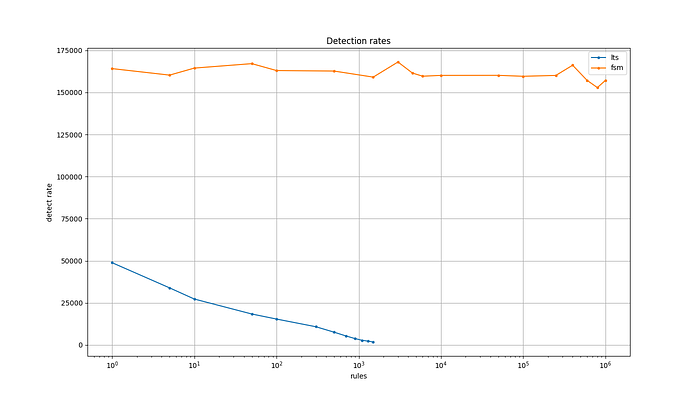
To benchmark my algorithm, I have compared the performance of the FSM approach with the basic boolean-tree algorithm discussed at “A basic algorithm” above, coding both in Python. The plot below shows the number of rules in use as the x-axis, and the event handling rate as the y-axis. This is a way to show how the number of rules in use affects event throughput. The orange line represents the performance of the FSM. You can see that the number of rules in use has very little affect on algorithm throughput. Note logarithmic scale on the x-axis.
下图将使用中的规则数显示为 x 轴,将事件处理率显示为 y 轴。这是一种显示正在使用的规则数量如何影响事件吞吐量的方法。橙色线代表 FSM 的性能。您可以看到使用的规则数量对算法吞吐量的影响很小。注意 x 轴上的对数刻度。
This was run on VirtualBox on my old MacBook, expect better performance from a cloud VM, for instance.
That’s a very quick look at performance, maybe I’ll do a follow-up article on performance later.
Conclusion
In this article I have discussed:
- How boolean expressions can be represented as trees
- Mapping boolean expressions to finite state machines
- How the use of an FSM simplifies detection logic and enables performance advantages
- How to use multiple FSMs for evaluation of concurrent boolean expressions
- That the FSM approach is implemented in the open source cyberprobe project



 浙公网安备 33010602011771号
浙公网安备 33010602011771号