单调栈算法模板
单调栈模板:
单调栈模板:
for (遍历这个数组)
while (栈不为空 && 栈顶元素<或者>当前元素)
栈顶元素出栈
更新结果
当前数据入栈
例如单调递增的stack,python实现就是:
stack = []
for i in range(0, len(arr)):
while stack and stack[-1] > arr[i]:
stack.pop()
# do something to find result 常用要结合stack pop的元素和i的位置,更有甚者还要看栈顶也就是stack[-1]来综合计算
stack.append(arr[i])
变种:单调队列,见: https://www.cnblogs.com/bonelee/p/16988251.html
84. 柱状图中最大的矩形
https://leetcode.cn/problems/largest-rectangle-in-histogram/
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:

输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
示例 2:

输入: heights = [2,4] 输出: 4
提示:
1 <= heights.length <=1050 <= heights[i] <= 104
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
heights = [0] + heights + [0]
ans = 0
stack = []
for i in range(0, len(heights)):
while stack and heights[stack[-1]] > heights[i]:
pos = stack.pop()
square = heights[pos] * (i - 1 - stack[-1] )
# print(heights[pos], i, stack[-1], square)
ans = max(ans, square)
stack.append(i)
return ans
为啥是(i - 1 - stack[-1] )?而不是 i - pos?
(1)对于正常情形:只需要向右边跨越的矩形面积,例如下图数组下标2对应的元素5,其对应的矩形面积是10,只需要跨2个格子,只有右边的格子比它高,所以只能往右跨越。
计算方法:单调栈里是[1,5,6],遇到2的时候,应该从单调栈里pop 6和5,而pop 5的时候,就可以计算高度为5的最大面积 = 5(高度) x 2(宽度,等于元素2的下标 - 元素4的下标,也等于元素2的下标 - 1 - 元素1的下标),如下图所示:

(2)对于需要横跨左右的矩形面积,例如下图下标为2的元素1,其对应的最大矩形是1(高度)x6(宽度),宽度6向右跨域了4个格子,向左跨越了1个格子,加上自己的1个格子,一共6个。对于这种场景,我们看看stack里的数据情况,stack=[0,1],遇到的元素是0,则在pop 1的时候,宽度如何计算呢?见下第二个图说明!
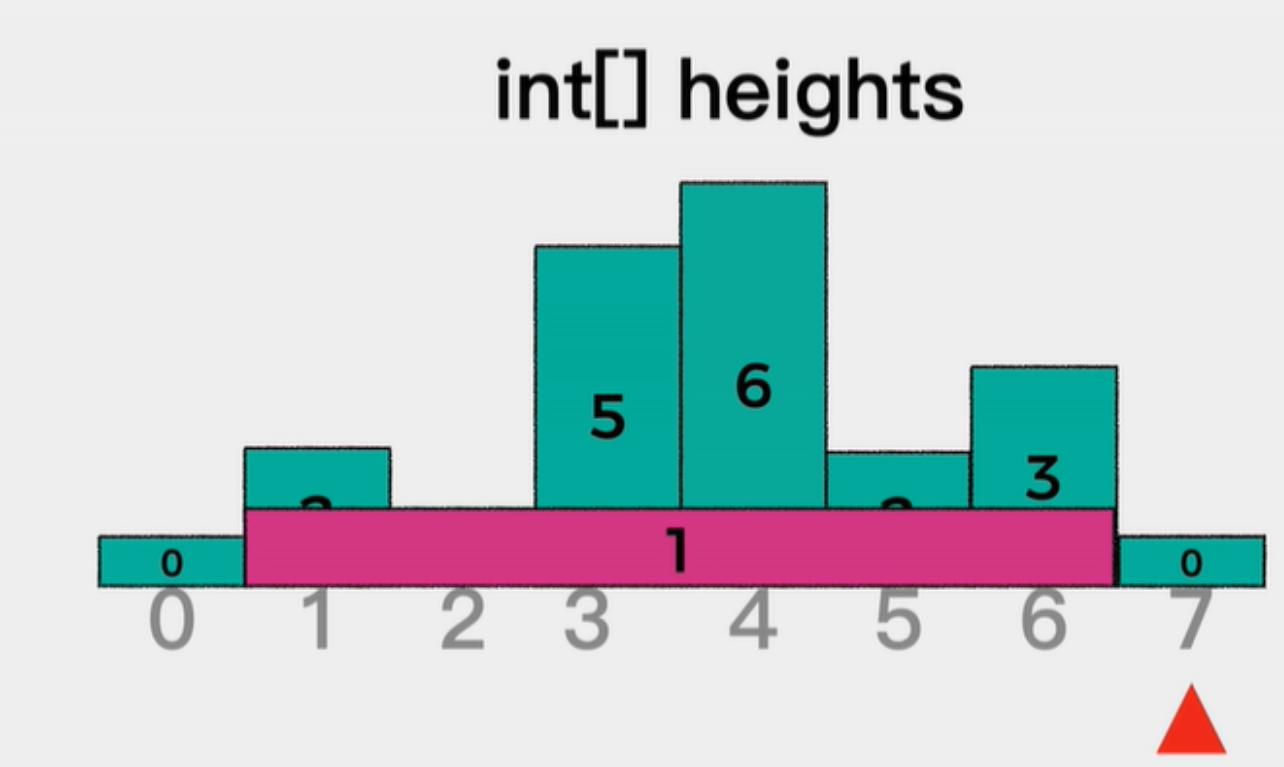

本质:因为stack里存储是【0,1】,元素1的面积要向左去跨越第一个比它矮小的格子!所以就只能是stack pop本身以后,再取栈顶元素就是正好比它小的格子了。
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5] 输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
class Solution:
def trap(self, height: List[int]) -> int:
stack = []
ans = 0
for i in range(0, len(height)):
while stack and height[stack[-1]] < height[i]:
pos = stack.pop()
if not stack: # 前面没有东西了,表明全是上升的格子
continue
w = i - stack[-1] - 1
h = min(height[i], height[stack[-1]]) - height[pos]
water = w * h # 物理含义:height[pos]和height[i], height[stack[-1]]三根柱子能够积蓄的水
ans += water
stack.append(i)
return ans
物理含义:water = w * h 如下图所示:

52 · 下一个排列【不使用stack也可以】
给定一个整数数组来表示排列,按升序找出其下一个排列。
排列中可能包含重复的整数
样例 1:
输入:
数组 = [1]输出:
[1]解释:
只有一个整数,下一个排列是自己。
样例 2:
输入:
数组 = [1,3,2,3]输出:
[1,3,3,2]解释:
[1,3,2,3]的下一个排列是[1,3,3,2]。
样例 3:
输入:
数组 = [4,3,2,1]输出:
[1,2,3,4]解释:
没有字典序更大的排列时,输出字典序最小的排列。
最近的解法:
class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
def find_swap_pos():
i = len(nums) - 1
while i - 1 >= 0 and nums[i] <= nums[i - 1]:
i -= 1
return i - 1
def find_swap_pos2(pos):
j = pos + 1
while j < len(nums) and nums[j] > nums[pos]:
j += 1
return j - 1
def swap(m, n):
while m < n:
nums[m], nums[n] = nums[n], nums[m]
n -= 1
m += 1
pos = find_swap_pos()
if pos < 0:
swap(0, len(nums) - 1)
return
pos2 = find_swap_pos2(pos)
nums[pos], nums[pos2] = nums[pos2], nums[pos]
swap(pos + 1, len(nums) - 1)
使用stack写的话:
from typing import (
List,
)
class Solution:
"""
@param nums: A list of integers
@return: A list of integers
"""
def next_permutation(self, nums: List[int]) -> List[int]:
# write your code here
# 123213 4510 ==> 123213 5014
# 123213 476410 ==> 123213 601447
# 考察单调栈,三步:
# 1、从后向前升序,找到第一个降序数字,对于123213 476410则找到4是第一个降序数字
# 2、然后找到升序里第一个大于它的数字,就是6了!
# 3、然后交换4和6,则变成123213 674410,最后将74410反转下排序就是123213 601447
if not nums or len(nums) == 1:
return nums
i = len(nums) - 2
stack = [len(nums)-1]
while i >= 0 and stack and nums[stack[-1]] <= nums[i]:
stack.append(i)
i -= 1
if i < 0:
return nums[::-1]
# assert nums[i] < stack[-1]
pos1 = pos2 = i
while stack and nums[stack[-1]] > nums[i]:
pos2 = stack.pop()
nums[pos1], nums[pos2] = nums[pos2], nums[pos1]
i, j = pos1+1, len(nums)-1
while i < j:
nums[i], nums[j] = nums[j], nums[i]
i += 1
j -= 1
return nums



 浙公网安备 33010602011771号
浙公网安备 33010602011771号