对比学习(Contrastive Learning)综述——无监督学习+特征抽象,损失函数:同类尽可能近,不同类尽可能远,思想和聚类类似
对比学习(Contrastive Learning)综述
A.引入
A.引入
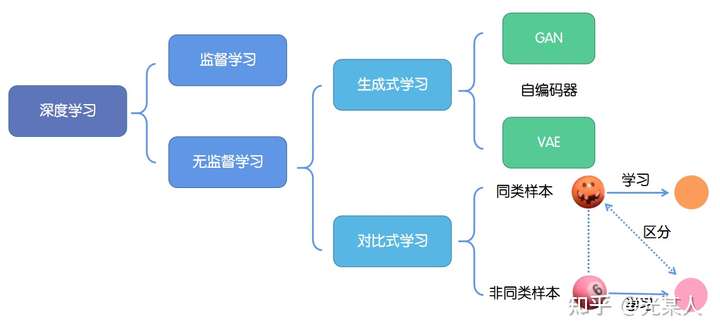
深度学习的成功往往依赖于海量数据的支持,其中对于数据的标记与否,可以分为监督学习和无监督学习。
1. 监督学习:技术相对成熟,但是对海量的数据进行标记需要花费大量的时间和资源。
2. 无监督学习:自主发现数据中潜在的结构,节省时间以及硬件资源。
2.1 主要思路:自主地从大量数据中学习同类数据的相同特性,并将其编码为高级表征,再根据不同任务进行微调即可。
2.2 分类:
2.2.1生成式学习
生成式学习以自编码器(例如GAN,VAE等等)这类方法为代表,由数据生成数据,使之在整体或者高级语义上与训练数据相近。
2.2.2对比式学习
对比式学习着重于学习同类实例之间的共同特征,区分非同类实例之间的不同之处。
与生成式学习比较,对比式学习不需要关注实例上繁琐的细节,只需要在抽象语义级别的特征空间上学会对数据的区分即可,因此模型以及其优化变得更加简单,且泛化能力更强。
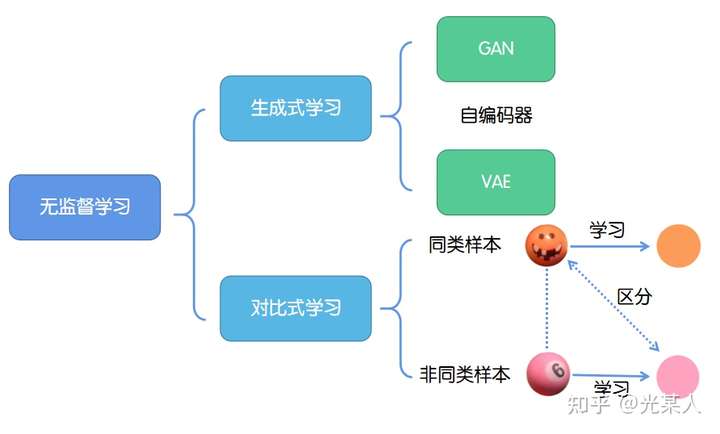
对比学习的目标是学习一个编码器,此编码器对同类数据进行相似的编码,并使不同类的数据的编码结果尽可能的不同。
3. 近况
最近深度学习两巨头 Bengio 和 LeCun 在 ICLR 2020 上点名 Self-Supervised Learning(SSL,自监督学习) 是 AI 的未来,另外,Hinton 和 Kaiming 两位神仙也在这问题上隔空过招,MoCo、SimCLR、MoCo V2 打得火热,这和 BERT 之后,各大公司出 XL-Net、RoBerta 刷榜的场景何其相似。
4.感谢
写这篇综述,花了大概一个多月时间整理【刚大二,有篇复旦的论文确实看不懂,这里就没写】,感谢各位大佬的博客,给了我莫大的帮助,还有学长
和同学 的鼓励,才让我有信心肝完这篇国内资料不那么完善的综述。
本文对目前的对比学习相关,尤其是NLP方面的工作进行较为全面的介绍,希望能够为感兴趣的同学提供一些帮助。
B. 对比引入
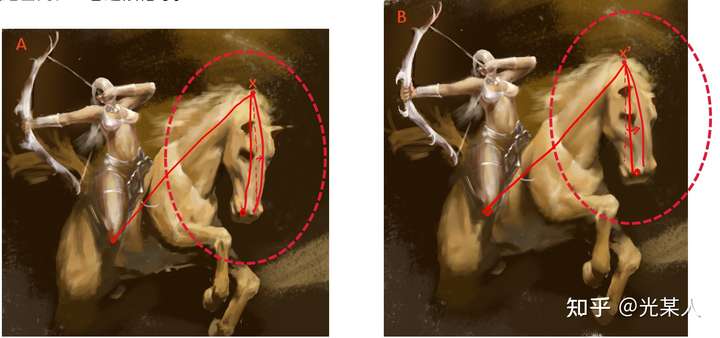
【拿我的画举个例子】我们可以看到下面两张图的马头和精细程度都是不同的,但是我们显然能判断这两张是类似的图,这是为什么呢

对于某个固定锚点x来说,其位置是由与其他点相对位置决定的,而不是画布的绝对位置。==》特征抽象
A中与 x 邻近的点在B图中相应点距 x' 距离小,A中与 x 相距较远的点在B图中相应点距 x' 距离大。
在一定误差范围内,二者近似相等。
可以这么认为,通过对比学习,忽略了细节,找到并确定所以关键点相对位置。
C. 聚类思想
在这里,我们将之前的想法进行抽象,用空间考虑对比学习。
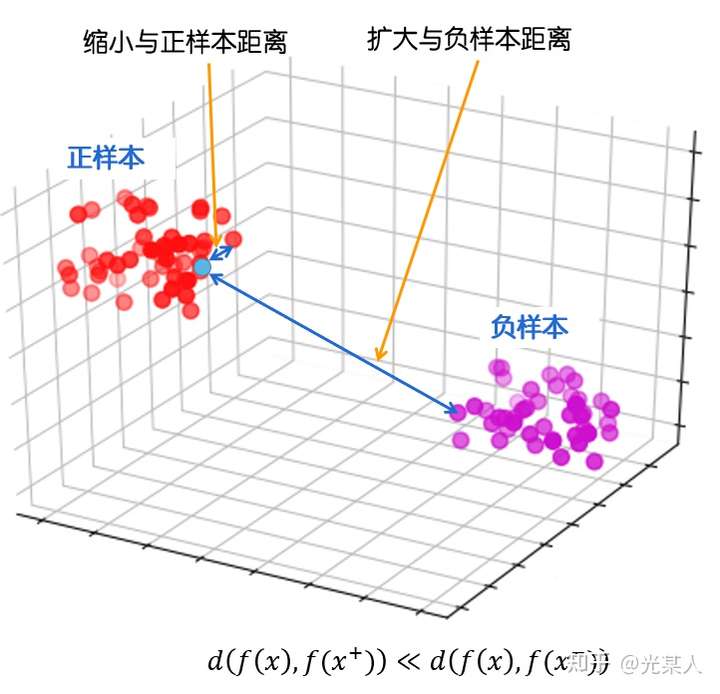
最终目标:
缩小与正样本间的距离,扩大与负样本间的距离,使正样本与锚点的距离远远小于负样本与锚点的距离,(或使正样本与锚点的相似度远远大于负样本与锚点的相似度),从而达到他们间原有空间分布的真实距离。
- 丈量二者距离:欧几里得距离,余弦相似度,马氏距离(没人试过,但原理是一样的)
- 目标:给定锚点,通过空间变换,使得锚点与正样本间距离尽可能小,与负样本距离尽可能大==》抽象是如此做的!!!==》从这个实现看,对于图像缩放可能有帮助,但是其他场景CNN做卷积池化效果不更好?==》用在流量分析里咋搞?
D.对比思想
动机:人类不仅能从积极的信号中学习,还能从纠正不良行为中获益。
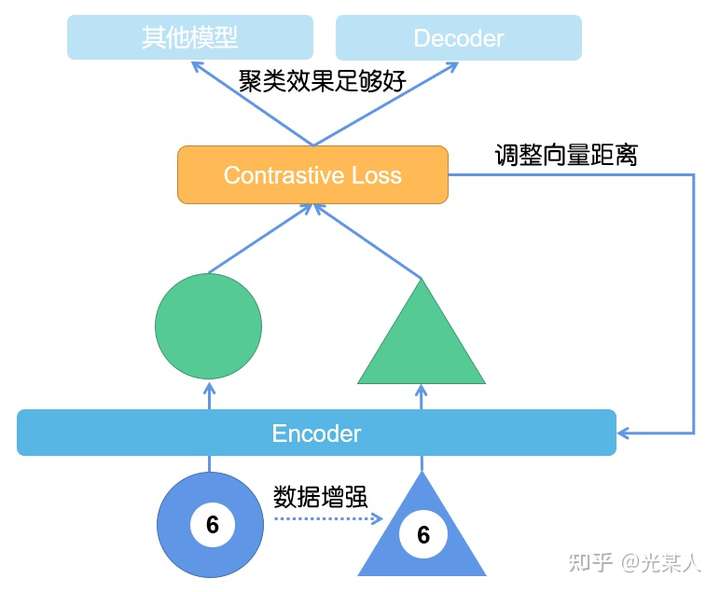
对比学习其实是无监督学习的一种范式。根据经典的SIMCLR,我在这里就直接提供了对比学习中模型的常见形式。
E. 对比损失【重要*数学警告】
本章的数学公式可以只看结论(NCE可以不看),如果想了解细节请仔细阅读【附录】,如果不懂可以评论私信,或者移步参考博客学习。
1. 欧几里得距离
在线性空间中,上述相似度就可以表示为二者向量间的欧几里得距离:
2. 对比损失定义
由Hadsell, R. , Chopra, S. , & Lecun, Y. . (2006)提出[1] ,原文只是作为一种降维方法:只需要训练样本空间的相对关系(对比平衡关系)即可在空间内表示向量。
损失定义如下:
为了下文方便解释,这里的参数详细解释如下:
:网络权重;
:标志符,
:是
与
在潜变量空间的欧几里德距离。
:表示第i组向量对。
:研究中常常在这里做文章,定义合理的能够完成最终目标的损失函数往往就成功了大半。
2.1 细节定义
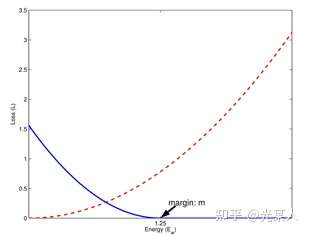
只需满足红色虚线趋势。
只需满足蓝线趋势【都有趋于0的区域】。
2.2 过程/主流程
原文类比弹性势能,将正负样本分类讨论。
正样本:
当与锚点是正样本时,由于对比思想,二者之间会逐渐靠近。原文将它假设成一个原长 的弹簧,那么就会将正样本无限的拉近,从而完成聚类。
将锚点设为势能零点:
那么 E 即可作为 ,且满足定义要求:
负样本
当与锚点是负样本时,由于对比思想,二者之间会逐渐原理。原文将它假设成一个原长 的弹簧,那么就会将负样本至少拉至m,从而完成划分。
将锚点设为势能零点:
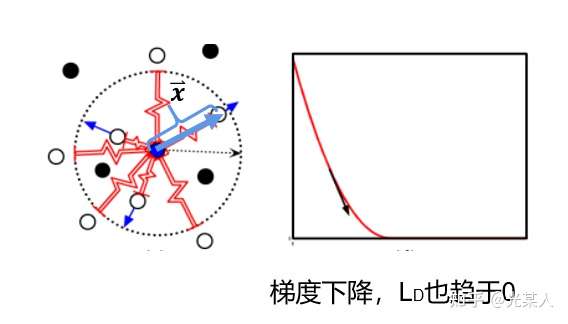
L原定义:
这样我们就获得了Loss函数最基本的定义:
当Y=0,调整参数最小化 。
当Y=1,设二者向量最大距离为m,
如果 , 则增大两者距离到m;
如果 ,则不做优化。
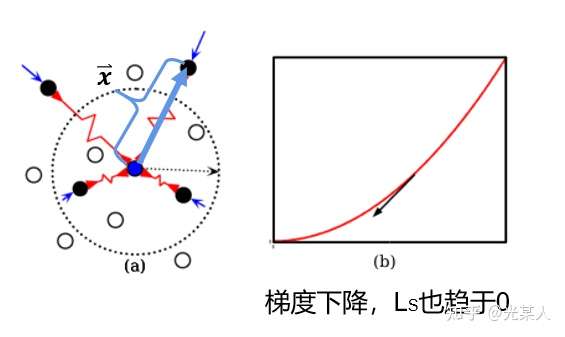
空间角度:
空间内点间相互作用力动态平衡。
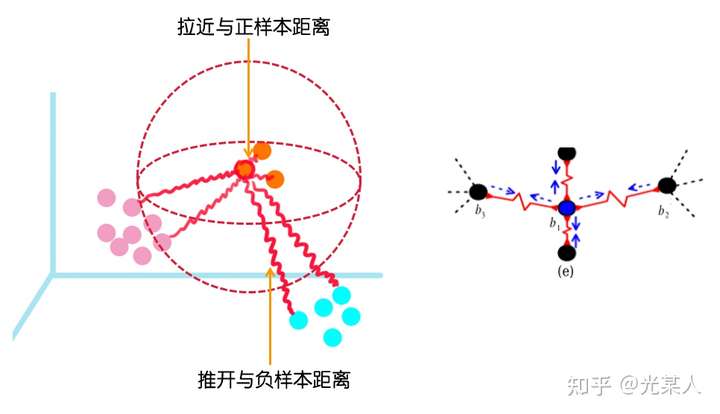
2.3 效果
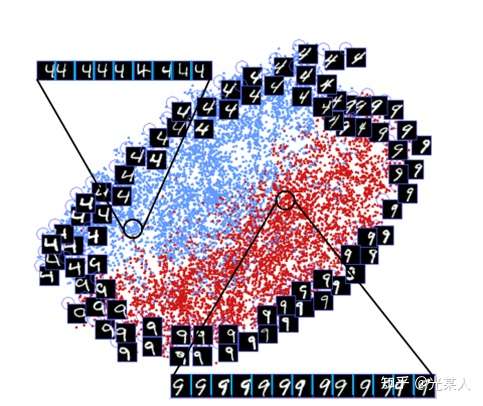
我们可以看到,和4不那么像的9会被拉远离4,和4相似的9会在交界面上十分接近地分布。这和我们的的对比想法是一致的。
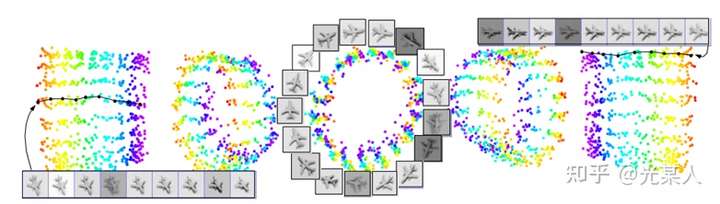
同时,该论文还发现许多对比学习中有趣的现象。
不同光照下,不同角度下,像素间欧氏距离尽管很远,但是能聚集在一个环上。
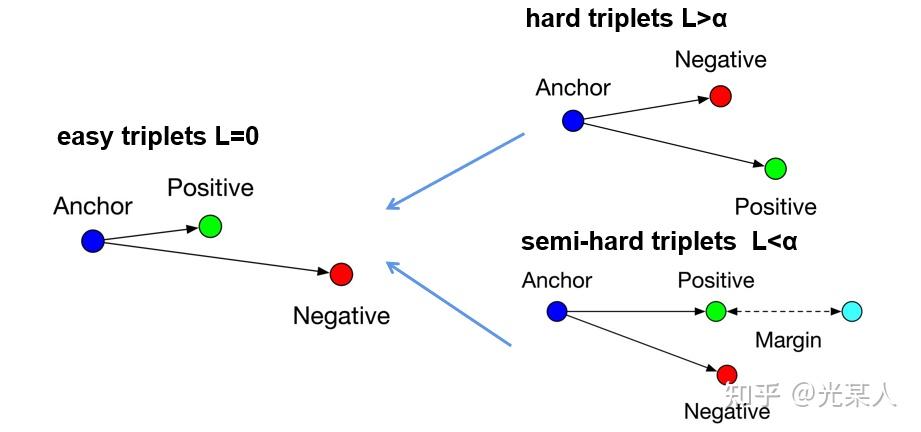
3. Triplet Loss
(简化版原方法)
结论
我们将三元组重新描述为 。
那么三元组的总体距离可以表示为:【近年论文好像也有沿用的,比较经典】
相较定义来说,Triplet Loss认为,假如所有正样本之间无限的拉近,会导致聚类过拟合,所以,就只要求
当然在比例尺上看来, 也会趋于0。
原文将所有三元组的状态分为三类:
- hard triplets
正样本离锚点的距离比负样本还大 - semi-hard triplets
正样本离锚点的距离比负样本小,但未满足 - easy triplets
满足
前两个状态会通过loss逐渐变成第三个状态。
4. NCE Loss
【注:后续研究并没有怎么使用原始的NCELoss,而是只使用这里的结论,这里引入是为了说明应该多采用负样本。】
之前从向量空间考虑,NCE从概率角度考虑【原证明为贝叶斯派的证法】,NCE是对于得分函数的估计,那也就是说,是对于你空间距离分配的合理性进行估计。
总之NCE通过对比噪声样本与含噪样本,从而推断真实分布。
【与对比学习思想一致,可以当做是另一角度】
结论
越大,约接近NCE 对于噪声分布的依赖程度也就越小,越接近真实期望。
5. 互信息
在预测未来信息时,我们将目标x(预测)和上下文c(已知)编码成一个紧凑的分布式向量表示(通过非线性学习映射),其方式最大限度地保留了定义为的原始信号x和c的互信息
通过最大化编码之间互信息(它以输入信号之间的MI为界),提取输入中的隐变量。
互信息往往是算不出来的,但是我们这里将他进行估计,通过不同方法进行估计,从而衍生出自监督的两种方式:生成式和对比式【详见A 2.2.2】
互信息上界估计:减少互信息,即VAE的目标。
互信息下界估计:增加互信息,即对比学习(CL)的目标。【后来也有CLUB上界估计和下界估计一起使用的对比学习。】
6. InfoNCE Loss
具体详见CPC论文1.3节。
通过二者互信息【详见附录】来衡量二者距离/相似度,可逼近其下界。
结论
后续研究
后续研究的核心往往就聚焦于的两个方面:
- 如何定义目标函数?【详见附录】
- 简单内积函数
- InfoNCE【近年火热】
- triplet 【近年火热】 【知乎的问题,后边的s函数的负号上标可能消失】
- 如何构建正实例对和负实例对?
这个问题是目前很多 paper 关注的一个方向,设计出合理的正实例与负实例对,并且尽可能提升实例对,才能表现的更好。
F. 基础论文
1. CPC
论文标题:Representation Learning with Contrastive Predictive Coding
论文链接:https://arxiv.org/abs/1807.03748
代码链接:https://github.com/davidtellez/contrastive-predictive-coding
很多时候,很多数据维度高、label相对少,我们并不希望浪费掉没有label的那部分data。所以在label少的时候,可以利用无监督学习帮助我们学到数据本身的高级信息,从而对下游任务有很大的帮助。
Contrastive Predictive Coding(CPC) 这篇文章就提出以下方法:
- 将高维数据压缩到更紧凑的隐空间中,在其中条件预测更容易建模。
- 用自回归模型在隐空间中预测未来步骤。
- 依靠NCE来计算损失函数(和学习词嵌入方式类似),从而可以对整个模型进行端到端的训练。
- 对于多模态的数据有可以学到高级信息。
可以利用一定窗口内的 和
作为正实例对,并从输入序列之中随机采样一个输入作为
负实例。
1.1 问题描述

给定声音序列上下文 ,由此我们推断预测
位置上的声音信号。题目假设,声音序列全程伴随有噪音。为了将噪音序列与声音序列尽可能的分离编码,这里就随机采样获得
代替
位置信号,作为负样本进行对比学习。
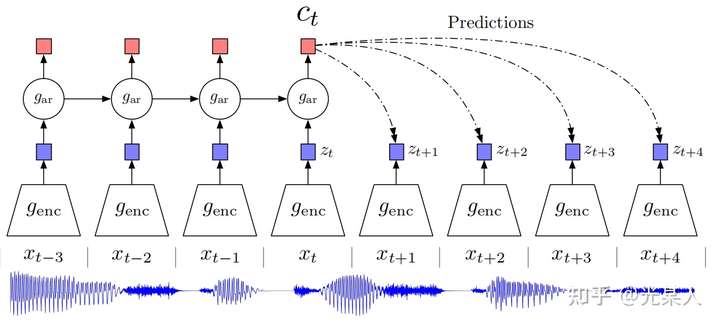
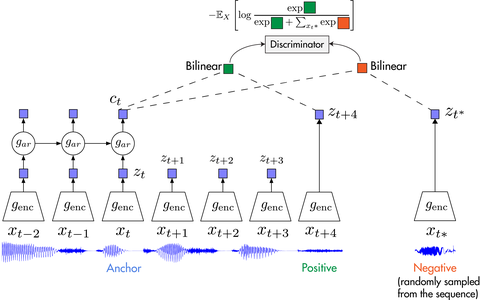
1.2 CPC
下图说明了 CPC 的工作过程:
首先我们在原信号上选取一些时间窗口,对每一个窗口,通过encoder ,得到表示向量
。
通过自回归模型:
,从而生成上下文隐变量
。
然后通过Bi-linear:【采用 和
从而能够压缩高维数据,并且计算
和
的未来值是否符合】
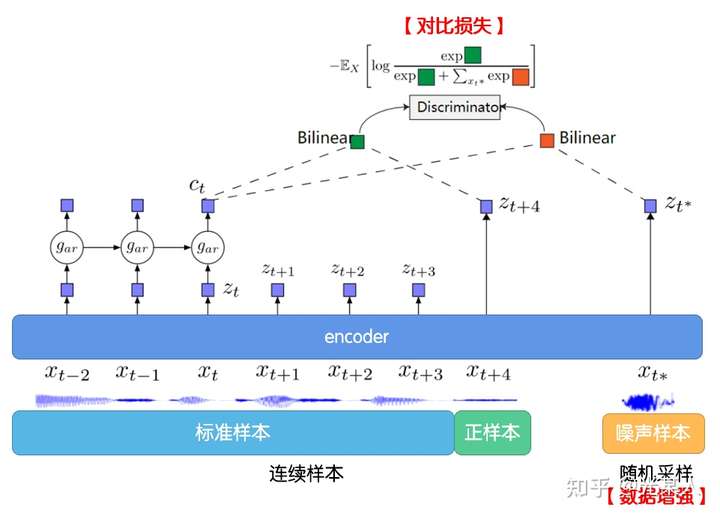
1.3 InfoNCE Loss
CPC用到了NCE Loss, 并推广为InfoNCE:(证明见【附录】)
选取 ,这里面只有一个正样本对
来自于
,即声音原本的信号,其他N-1个均是负样本(噪声样本)来自于
,即随机选取的信号片段。
损失函数定义如下:【 f 可自由定义,甚至为MLP】
我们用softmax的思路来理解这个损失函数, 越大,
应该越接近于0(越接近最大值),而损失就越小。
回到对比学习的思想,W将做c到z的映射, 均经过归一化,那么,二者余弦相似度为
,这样
,即可看做softmax,将
正样本的值加大,负样本值缩小。
2. MoCo
论文标题:Momentum Contrast for Unsupervised Visual Representation Learning
论文来源:CVPR 2020
论文链接:https://arxiv.org/abs/1911.05722
代码链接:https://github.com/facebookresearch/moco
本文提出了高效的对比学习的结构。使用基于 MoCo 的无监督学习结构学习到的特征用于 ImageNet 分类可以超过监督学习的性能。证明了无监督学习拥有巨大的潜力。
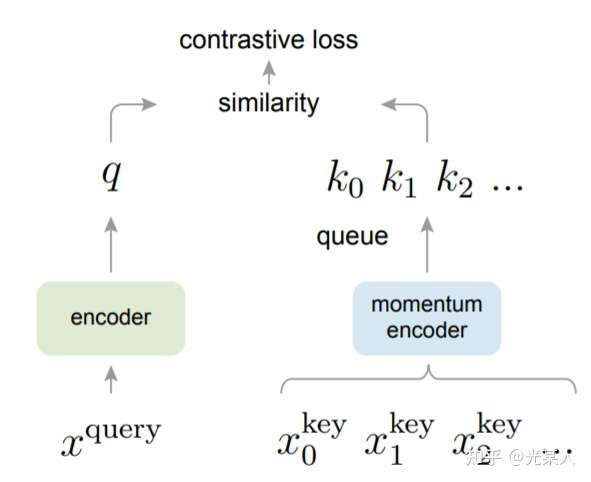
受NLP任务的启发,MOCO将图片数据分别编码成查询向量和键向量,即,查询 q 与键队列 k ,队列包含单个正样本和多个负样本。通过 对比损失来学习特征表示。
主线依旧是不变的:在训练过程中尽量提高每个查询向量与自己相对应的键向量的相似度,同时降低与其他图片的键向量的相似度。
MOCO使用两个神经网络对数据进行编码:encoder和momentum encoder。
encoder负责编码当前实例的抽象表示。
momentum encoder负责编码多个实例(包括当前实例)的抽象表示。
对于当前实例,最大化其encoder与momentum encoder中自身的编码结果,同时最小化与momentum encoder中其他实例的编码结果。
2.1 InfoNCE Loss
这个Loss只能更新q向量的encoder。如果同时更新q和k没有意义。
交叉熵损失:
交叉熵损失(Cross-entropy Loss) 是分类问题中默认使用的损失函数:
分类模型中,最后一层一般是linear layer+softmax。所以如果将之前的特征视为, linear layer的权重视为
,则有:
每个权重矩阵 事实上代表了每一类样本其特征值的模板(根据向量乘法我们知道越相似的两个向量其内积越大)。
实际上,现有的分类问题是通过一系列深度网络提取特征,然后依据大量的样本学习到一个有关每一类样本特征的模板。在测试的阶段则将这个学到的特征模板去做比对。
非参数样本分类:
所谓非参数样本分类,则是将每个计算出的样本特征作为模板,即看做是计算所得的样本特征模板。
对比损失:
我们最终的目标还是不变的:
这里与CPC类似地,我们使用cosine距离,假设已经归一化特征值,则优化上式实际上等同于最大化下式中的softmax概率,
假设其中有一个正样本 其余均是负样本,则根据 InfoNCE Loss表示为:
其中 和
可以有多种构造方式,比如对图像进行裁剪变色等随机变化。
但是呢,实现上来说,将 看做一体为
,那么
,即为交叉熵损失。
2.2 Memory Bank
由于对比学习的特性,参与对比学习损失的实例数往往越多越好,但Memory Bank中存储的都是 encoder 编码的特征,容量很大,导致采样的特征具有不一致性(是由不同的encoder产生的)。
所以,对所有参与过momentum encoder的实例建立动态字典(dynamic dictionary)作为Memory Bank,在之后训练过程中每一个batch会淘汰掉字典中最早被编码的数据。
2.3 Momentum 更新
在参数更新阶段,MOCO只会对encoder中的参数进行更新。
由于Memory Bank,导致引入大量实例的同时,会使反向传播十分困难,而momentum encoder参数更新就依赖于Momentum 更新法,使momentum encoder的参数逐步向encoder参数逼近:
其中 ,
指encoder部分的参数。
下图形式化的表示了三种结构,end-to-end,memory-bank和MoCo的区别。MoCo的特点是:
(1)用于负采样的队列是动态的
(2)用于负样本特征提取的编码器与用于query提取的编码器不一致,是一种Momentum更新的关系。
(3)与Memory Bank类似,NCE Loss只影响 Query ,不更新key。
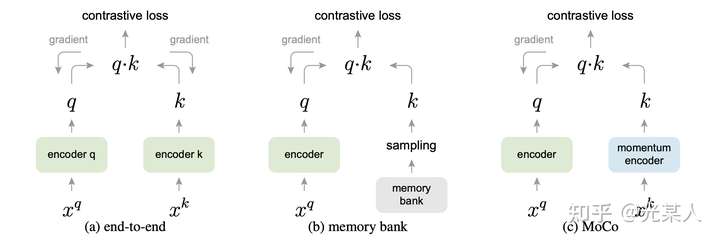
2.4 代码流程

3. SimCLR
论文标题:A Simple Framework for Contrastive Learning of Visual Representations
论文链接:https://arxiv.org/abs/2002.05709
代码链接:https://github.com/google-research/simclr
写在前面
由于最近开始在看对比学习的一些相关工作,想把学到的东西记录一下。本文前半部分基于Ankesh Anand关于Contrastive Learning的blog中的内容,想看原文的可以移步下面链接:
在学习的过程中也参考了下面两篇文章:
好的,下面正式开始~
自监督学习
要说到对比学习,首先要从自监督学习开始讲起。自监督学习属于无监督学习范式的一种,特点是不需要人工标注的类别标签信息,直接利用数据本身作为监督信息,来学习样本数据的特征表达,并用于下游任务。
那么,自监督学习有什么优势呢?
目前机器学习主流的方法大多是监督学习方法,这类方法依赖人工标注的标签,这会带来一些缺陷:
- 数据本身提供的信息远比稀疏的标签更加丰富,因此使用有监督学习方法训练模型需要大量的标签数据,并且得到的模型有时候是“脆弱”的
- 有监督学习通过标签训练得到的模型往往只能学到一些任务特定的知识,而不能学习到一种通用的知识,因此有监督学习学到的特征表示难以迁移到其他任务
而自监督学习能够很好地避免上面的问题,因为自监督学习直接使用数据本身来提供监督信息来指导学习。
自监督学习分类
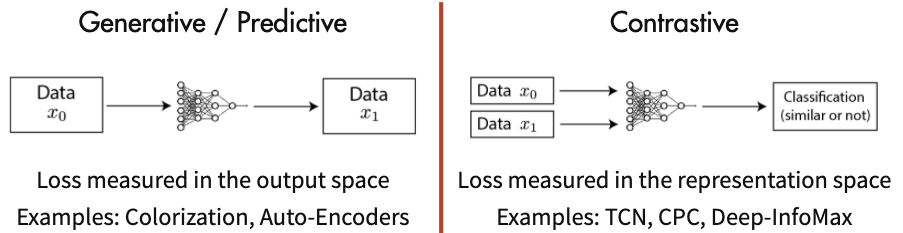
当前自监督学习可以被大致分为两类:
- Generative Methods
- Contrastive Methods
![]() Generative Methods and Contrastive Methods
Generative Methods and Contrastive Methods
Generative Methods(生成式方法)这类方法以自编码器为代表,主要关注pixel label的loss。举例来说,在自编码器中对数据样本编码成特征再解码重构,这里认为重构的效果比较好则说明模型学到了比较好的特征表达,而重构的效果通过pixel label的loss来衡量。
Contrastive Methods(对比式方法)这类方法则是通过将数据分别与正例样本和负例样本在特征空间进行对比,来学习样本的特征表示。Contrastive Methods主要的难点在于如何构造正负样本。
那么,Contrastive Methods有什么优势呢?
这里举一个例子来说明,Epstein在2016年做了一个实验:让受试者画出美元的图像,越详细越好,下图是受试者画出来的美元图像。
左图是受试者根据印象画出来的美元,右图则是让受试者照着美元画出来的。可以看到,左图画出来的美元图虽然不够详细,但已经充分具备一张美元的判别性信息,因此我们可以把它识别成美元。事实上,我们并不需要见到一张美元所有详细的信息,而仅仅通过一些关键的特征就可以识别出来。
同理,相比起Generative Methods需要对像素细节进行重构来学习到样本特征,Contrastive Methods只需要在特征空间上学习到区分性。因此Contrastive Methods不会过分关注像素细节,而能够关注抽象的语义信息,并且相比于像素级别的重构,优化也变得更加简单。
对比学习一般泛式
对任意数据 ,对比学习的目标是学习一个编码器
使得:
其中 是和
相似的正样本,
是和
不相似的负样本,score是一个度量函数来衡量样本间的相似度。
如果用向量内积来计算两个样本的相似度,则对比学习的损失函数可以表示成:
其中对应样本 有1个样本和N-1个负样本。可以发现,这个形式类似于交叉熵损失函数,学习的目标就是让
的特征和正样本的特征更相似,同时和N-1个负样本的特征更不相似。在对比学习的相关文献中把这一损失函数称作InfoNCE损失。也有一些其他的工作把这一损失函数称为multi-class n-pair loss或者ranking-based NCE。
对比学习相关论文
更新中



 Generative Methods and Contrastive Methods
Generative Methods and Contrastive Methods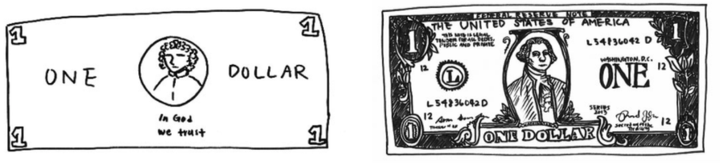

 浙公网安备 33010602011771号
浙公网安备 33010602011771号