M5P算法——本质上就是分段线性回归的树类算法
数据挖掘之一——M5P树状回归演算法
如果哪天你看到了这个文章，说明你是xixi，真怀念一起读博士的日子啊。M5P树状回归演算法可根据资料的分布建立多种回归模型，依据输入资料的不同来决定适用的回归模型。 比起传统的线性回归，M5P能够准确预测非线性的资料，而且规则与回归模型容易解读。 相较于类神经网路和支持向量机等黑箱演算法，白箱演算法的M5P更容易用于研究结果的解释上。
用数值来预测数值的问题叫做「回归」(regression)，而「回归」的经典演算法是线性回归(Linear Regression) 。 线性回归能够有效处理具有明确线性规律的资料，像是纬度的高低跟气温之间的关系 ，这可以让我们容易用多元回归来解释资料的规律 。 但是若资料呈现非线性的分布，那线性回归的效果就很差。 举例来说，月份跟气温的关系就不是单纯的线性关系。 较小跟较大的月份接近冬季，气温较低；位于中间的月份接近夏季，气温较高，这样的情况就是非线性资料。
处理非线性资料时，常见的做法会采用类神经网路( 多层次感知机或深度学习，也就是现在流行的AI)或是支持向量机的回归演算法SMOreg 。 但是这些黑箱演算法所建立的预测模型无法让人解读，对于解释研究结果的帮助有限。这时候，M5P树状回归预测演算法就是最佳的解决方案啦。下面举例进行说明：
下面这份散点图资料，共300个样本，涵盖25个地区从1月份到12月份的气温数据，25*12=300。
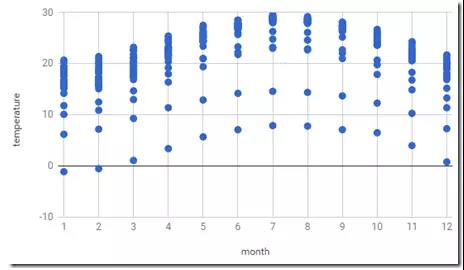
在month-temperature这份资料集中，我们要用月份month来预测气温temperature。 我将月份与气温画成了上面的散布图 。 每个月的气温有很多个点，这是因为地点不同所导致。 但这次的问题我们不考虑地点，仅看月份本身。 从散布图中可以看到不同月份的气温分布不太一样。 大致上来说，1月到3月、12月等的气温较低，6月到9月的气温较高，由此就可以看出冬季与夏季的差别。
这次是因为输入资料(属性)只有一个，而且是我们熟悉的月份，所以我们容易看出资料的规律。 若是在实际应用时，输入的资料往往高达二三十项。 要如何找出资料的规律，并建构出能够准确预测的模型，就要借助M5P演算法的技术了。接下来我们要对建模结果进行解读：
平均绝对误/ Mean absolute error
Mean absolute error平均绝对误，又称平均偏差 ，这是评估预测模型最简单的一个指标。 这表示所有预测值跟实际值之间偏差的平均。 以本例来说，若以M5P建立的预测模型，用月份来预测气温，则平均每次都会误差个3.2438度。
模型树/ Model tree
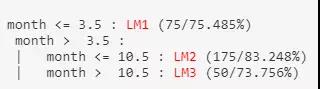
在本例中，M5P建构了3个线性回归模型，各别是LM1 、 LM2跟LM3 。 模型树用if-else的结构来表示什么时候适用哪种线性回归模型的时机。 用文字来叙述的话，上面的模型树的意思是：如month小于或等于3.5，则适用LM1模型来预测。
- 如果month大于3.5，则继续看下面的规则。
- 如果month小于或等于10.5，则适用LM2模型。
- 如果month大于10.5，则适用于LM3模型。
因为我们的month月份只有1到12，换句话说：
- 1月到3月：适用LM1
- 4月到10月：适用LM2
- 11月与12月：适用LM3
仔细一看，1月到3月、11月与12月偏向冬季，4月到10月则偏向夏季。 M5P在建构预测模型时就很敏锐地发现到了月份与季节的关系呢。
线性模型/ Linear Models
这里列出了三个线性模型，LM num: 1就是LM1、LM num: 2则是LM2、那LM num: 3就是指LM3。
非线性预测模型视觉化/ Model Visualization
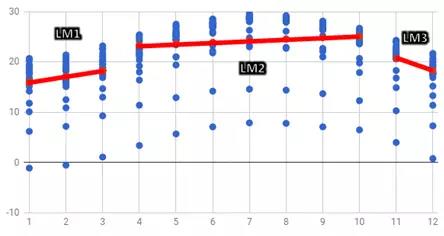
上图为LM1、LM2跟LM3画成折线图，并搭配原本月份与气温的散布图的整合结果。 蓝点为气温的实际值，红点与红线为3个线性模型的气温预测值。 3月到4月、10月到11月之间没有连线，这是因为他们适用于不同的模型。
比较实际值与预测模型之后，是不是更容易让你解释资料的变化了呢？ M5P就是这么好用啊。
相关推荐：
