通俗讲解Dirichlet分布和beta分布——Beta分布是二项分布的共轭先验,用大白话讲是,Beta分布描述了二项分布中p取值的可能性,那么Dirichlet分布久是描述多项式分布中p的可能性了
二项分布:
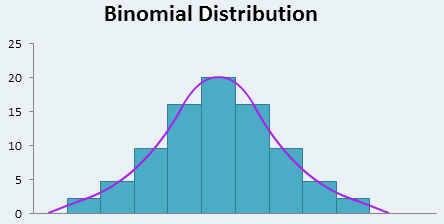
分布参数p,表示转化率的可能性。传统的频率学派会把实验总数中所有转化率的总数除以实验总数,得到这个p。以这个p为峰值获得一个类似高斯分布,大概像这样:
然而,贝叶斯学派不会假设p是固定不变的,他们会引入一个Beta分布作为二项分布的共轭先验,通过调整Beta分布参数,动态调整p的值.
Beta分布是什么?
Beta分布是二项分布的共轭先验。用大白话讲是,Beta分布描述了二项分布中p取值的可能性,这一分布相当合理:
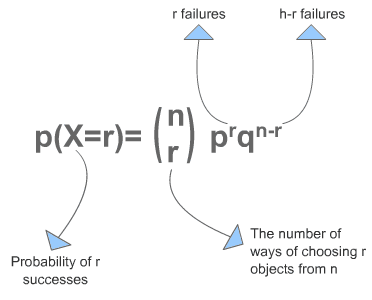
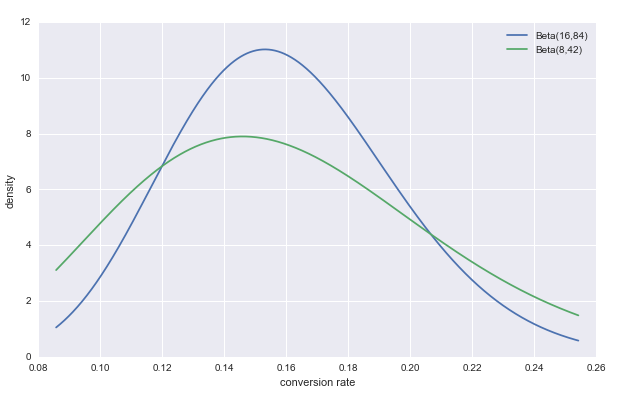
上图是一枚硬币抛100次有16次正面,和抛50次有8次正面的两个实验各自的Beta分布。可以注意到,Beta分布有两个参数α和β,α的现实意义就是16次正面,β的现实意义就是84次反面。
所以通俗地讲,Beta概率是对“正面概率应该为p”这件事情的概率分布。
有意思的是,上图抛100次有16次正面和抛50次有8次正面虽然只是实验规模不同,但是分布密度图是不一样的:
第一:频率学派观点是应该猜测正面概率p=0.16;贝叶斯学派观点是,以上两种情况的猜测p都小于0.16,因为实验次数越少,真实的正面和反面的差距就可能越大!
第二:实验次数越小,上面概率密度图应该越平缓(绿线),因为少的实验次数不能增大决策信心。而蓝色的100次实验,明显有更大的信心猜测p更接近0.16.
第三:实验次数越大,上面概率密度图的均值更应该接近0.16,符合大数定律。
是不是相当合理 !
很自然地,可以把Beta分布运用到我们日常的A/B测试。
但是写代码前,让我们先了解一个更有意义的话题:
什么是共轭先验?
关于共轭先验 需要记得两个关键点:
- 共轭关系是指似然概率和先验概率共轭!就是说,对于一个特定的似然函数,我们可以找到一个先验概率,叫做这个似然函数的共轭先验。
- 那符合什么条件才能叫共轭先验?找到这个先验概率后,如果符合:似然函数乘以先验概率后,得到的后验概率也是和先验概率一样的形式,那么就可以了!
如上图,先验概率是参数为![]() 的Beta分布,似然概率(Likelihood)是伯努利分布,那么后验概率计算后也是Beta分布,只是参数为
的Beta分布,似然概率(Likelihood)是伯努利分布,那么后验概率计算后也是Beta分布,只是参数为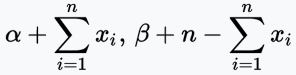
这里只是参数不同了而已,先验和后验都是Beta分布!这时我们就把Beta分布叫做伯努利分布的共轭先验!这里Beta分布的两个参数又叫超参数,因为Beta分布好似是伯努利分布的分布,可以通过不断迭代更新超参数,生成更好的伯努利分布或二项分布。
超参数相当容易迭代,因为先验和后验是一个形式。这一次的迭代结果可以作为下一次迭代的开始。
好了~ 最后让我们跑一些有趣的代码,来巩固A/B测试,Beta分布,以及“共轭先验”的相关知识。
模拟两个Beta分布,假设抛50次有8次正面(也可以理解为50个人的网页转化率):
实验次数太少,我们改进一下:
再画个PPF试试:
计算p-values指标:
p-values指标小于0.05,我们有信心相信银币反面概率更可能较大。
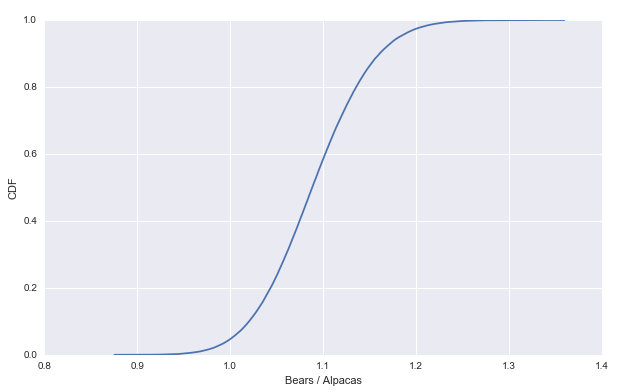
最后画个CDF图试试:
Cool ! 这就是今天的内容 下次见!
下面说多项分布:
多项分布
多项分布是二项分布的推广。多项分布的试验结果多于两个。例如足球比赛有:胜、平、负。
性质
(1)每次多项分布的试验结果有N种可能,但是只会出现一种结果。
(2)每次试验,每种结果都有各自发生的概率,所有结果发生的概率和为100%。
(3)各次试验相互独立,每次实验中结果概率都不会受影响。
公式
假设某个多项分布试验可能发生的结果数目为k(1,2....k)。根据历史数据每种结果
发生的概率分别为p1,p2...pk。现在进行n次多项分布试验,假设观测到结果为“1”的次
数有x1,结果为“2”的次数为x2,...,结果为“k”的次数为xk。

多项分布对每一个结果都有均值。
![]()
通俗理解Dirichlet分布及其实践
写在前面
最近项目中有一部分用到了Dirichlet分布及其采样,这个分布应该是本科阶段的概率论没有教过的吧(也可能是我上课走神😓)。于是,从头学习,整理如下。
Beta分布
要说Dirichlet分布之前,先了解下其特殊情况Beta分布。一言以蔽之,Beta分布是二项分布的分布。二项分布中的参数theta在Beta分布中,也被认为是一个随机变量,因此Beta分布是用来描述这个随机变量theta的。下面用知乎上一个通俗的例子来说明(我觉得这个例子讲得相当好)。更严谨的叙述参看PRML中相关章节。
用一句话来说,beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可能性大小。
举一个简单的例子,熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average),就是用一个运动员击中的球数除以击球的总数,我们一般认为0.266是正常水平的击球率,而如果击球率高达0.3就被认为是非常优秀的。现在有一个棒球运动员,我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率,用击中的数除以击球数,但是如果这个棒球运动员只打了一次,而且还命中了,那么他就击球率就是100%了,这显然是不合理的,因为根据棒球的历史信息,我们知道这个击球率应该是0.215到0.36之间才对啊。对于这个问题,我们可以用一个二项分布表示(一系列成功或失败),一个最好的方法来表示这些经验(在统计中称为先验信息)就是用beta分布,这表示在我们没有看到这个运动员打球之前,我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。接下来我们将这些先验信息转换为beta分布的参数,我们知道一个击球率应该是平均0.27左右,而他的范围是0.21到0.35,那么根据这个信息,我们可以取α=81,β=219。

这是因为:
- beta分布的均值是
αα+β=8181+219=0.27
- 从上图中,我们可以看到该分布主要落在(0.2,0.35)间,这就是从先验中得到的知识。
在这个例子里,我们的x轴就表示各个击球率的取值,x对应的y值就是这个击球率所对应的概率。也就是说beta分布可以看作一个概率的概率分布。那么有了先验信息后,现在我们考虑一个运动员只打一次球,那么他现在的数据就是”1中;1击”。这时候我们就可以更新我们的分布了,让这个曲线做一些移动去适应我们的新信息。beta分布在数学上就给我们提供了这一性质,他与二项分布是共轭先验的(Conjugate_prior)。所谓共轭先验就是先验分布是beta分布,而后验分布同样是beta分布。结果很简单:
其中α0和β0是一开始的参数,在这里是81和219。所以在这一例子里,α增加了1(击中了一次)。β没有增加(没有漏球)。这就是我们的新的beta分布Beta(81+1,219),我们跟原来的比较一下:

可以看到这个分布其实没多大变化,这是因为只打了1次球并不能说明什么问题。但是如果我们得到了更多的数据,假设一共打了300次,其中击中了100次,200次没击中,那么这一新分布就是:

注意到这个曲线变得更加尖,并且平移到了一个右边的位置,表示比平均水平要高。
一个有趣的事情是,根据这个新的beta分布,我们可以得出他的数学期望为:
这一结果要比直接的估计要小:
你可能已经意识到,我们事实上就是在这个运动员在击球之前可以理解为他已经成功了81次,失败了219次这样一个先验信息。
因此,对于一个我们不知道概率theta是什么的二项分布,而又有一些合理的猜测时,beta分布能很好的作为描述该概率theta的概率分布。
结论1:二项分布与Beta分布是共轭先验的。即Beta分布乘上一个二项分布的似然函数后,得到的后验分布仍然是一个Beta分布。
关于其的证明,可以参考reference中的链接。
Dirichlet分布
先给出一个结论:
结论2:Dirichlet分布就是由2种结果bernoulli trial导出的Beta分布外推到k种的一般情形。
详细一点地说,二项分布的分布是Beta分布,而二项分布的推广形式多项分布的分布就是Dirichlet分布。
结论3:Dirichlet分布与多项分布是共轭先验的。即Dirichlet分布乘上一个多项分布的似然函数后,得到的后验分布仍然是一个Dirichlet分布。
严谨的叙述参考PRML相关章节。
实践:Dirichlet分布的估计
即在给定多项分布中概率向量p的一些样本后,如何估计Dirichlet分布中的参数alpha。关于这个问题,Microsoft Research的Tom Minka给出了两种解决办法。无外乎都是极大似然法,两种方法的差异在于第一种方法是采用拟牛顿法来迭代求最大似然估计,而第二种方法则是稍微曲线救国了一下,先定义两个与alpha相关的值,通过先求这两个值从而求得alpha的最大似然估计,其中采用了EM的思想。具体细节可以参考其论文。
Minka大神同时也实现了其提出的两种方法的Matlab源码,而Eric J. Suh将这些算法又用Python实现了一遍,做成了一个独立的Python Package。我项目中就是直接用的这个,跪谢两位大神Orz!
Reference
https://github.com/tminka/fastfit
https://tminka.github.io/papers/dirichlet/minka-dirichlet.pdf
https://www.zhihu.com/question/30269898
https://mqshen.gitbooks.io/prml/Chapter2/multinomial/dirichlet_distribute.html
https://mqshen.gitbooks.io/prml/Chapter2/binary/beta_distribute.html
翻译改编自:tl;dr Bayesian A/B Testing with Python
参考文献:
#Bayesian Estimator
In [2]:
>>> import pandas as pd
>>> from pgmpy.models import BayesianModel
>>> from pgmpy.estimators import BayesianEstimator
>>> data = pd.DataFrame(data={'A': [0, 0, 1], 'B': [0, 1, 0], 'C': [1, 1, 0]})data.head()
Out[2]:
A B C
0 0 1
0 1 1
1 0 0
In [3]:
>>> model = BayesianModel([('A', 'C'), ('B', 'C')])
>>> estimator = BayesianEstimator(model, data)
>>> cpd_C = estimator.estimate_cpd('C', prior_type="dirichlet", pseudo_counts=[1, 2])
>>> print(cpd_C)╒══════╤══════╤══════╤══════╤════════════════════╕
│ A │ A(0) │ A(0) │ A(1) │ A(1) │
├──────┼──────┼──────┼──────┼────────────────────┤
│ B │ B(0) │ B(1) │ B(0) │ B(1) │
├──────┼──────┼──────┼──────┼────────────────────┤
│ C(0) │ 0.25 │ 0.25 │ 0.5 │ 0.3333333333333333 │
├──────┼──────┼──────┼──────┼────────────────────┤
│ C(1) │ 0.75 │ 0.75 │ 0.5 │ 0.6666666666666666 │
╘══════╧══════╧══════╧══════╧════════════════════╛
我们来看看为啥是这样?原始的数据分布:
A B C
0 0 1 ==》可以看到并没有0,0,0的分布?怎么办?这个时候dirichlet出现了,pseudo_counts=[1, 2]会加入先验分布,认为001出现1次,000出现2次。最终得到上表0.25,0.75的概率!
0 1 1 ==》可以看到并没有0,1,0的分布?怎么办?处理方式同上!
1 0 0==》可以看到并没有1,0,0的分布?处理方式同上!
此外,并没有看到110,111的分布,则pseudo_counts=[1, 2]会加入先验分布,认为110出现1次,111出现2次,则概率为1/3,2/3!
继续看一些例子:
利用训练数据学习
场景: 投硬币, 训练数据中, 有 30% 的正面朝上, 有 70% 的反面朝上. 我们使用极大似然估计和狄利克雷分布下贝叶斯参数先验估计硬币的条件概率分布.
生成数据:
import numpy as np import pandas as pd raw_data = np.array([0] * 30 + [1] * 70) data = pd.DataFrame(raw_data, columns=['coin'])
定义贝叶斯网:
from pgmpy.models import BayesianModel
from pgmpy.estimators import MaximumLikelihoodEstimator, BayesianEstimator
model = BayesianModel()
model.add_node('coin')
使用极大似然估计:
model.fit(data, estimator=MaximumLikelihoodEstimator)
print(model.get_cpds('coin'))
结果如下:
+---------+-----+ | coin(0) | 0.3 | +---------+-----+ | coin(1) | 0.7 | +---------+-----+
使用狄利克雷分布作为先验分布的贝叶斯推论:
model.fit(data, estimator=BayesianEstimator, prior_type='dirichlet', pseudo_counts={'coin': [50, 50]})
print(model.get_cpds('coin'))
因为(50+30)/(30+70+50+50)=0.4;(50+70)/(30+70+50+50)=0.6
结果如下:
+---------+-----+ | coin(0) | 0.4 | +---------+-----+ | coin(1) | 0.6 | +---------+-----+
更复杂的例子(学生例子)
学生例子中包含5个随机变量, 如下所示:
| 变量 | 含义 | 取值 |
|---|---|---|
| Difficulty | 课程本身难度 | 0=easy, 1=difficult |
| Intelligence | 学生聪明程度 | 0=stupid, 1=smart |
| Grade | 学生课程成绩 | 1=A, 2=B, 3=C |
| SAT | 学生高考成绩 | 0=low, 1=high |
| Letter | 可否获得推荐信 | 0=未获得, 1=获得 |
生成数据:
import numpy as np import pandas as pd raw_data = np.random.randint(low=0, high=2, size=(1000, 5)) data = pd.DataFrame(raw_data, columns=['D', 'I', 'G', 'L', 'S'])
定义模型:
from pgmpy.models import BayesianModel
from pgmpy.estimators import MaximumLikelihoodEstimator, BayesianEstimator
model = BayesianModel([('D', 'G'), ('I', 'G'), ('I', 'S'), ('G', 'L')])
model.fit(data, estimator=MaximumLikelihoodEstimator)
for cpd in model.get_cpds():
print("CPD of {variable}:".format(variable=cpd.variable))
print(cpd)
结果如下:
CPD of D: +------+-------+ | D(0) | 0.501 | +------+-------+ | D(1) | 0.499 | +------+-------+ CPD of G: +------+------+----------------+----------------+----------------+ | D | D(0) | D(0) | D(1) | D(1) | +------+------+----------------+----------------+----------------+ | I | I(0) | I(1) | I(0) | I(1) | +------+------+----------------+----------------+----------------+ | G(0) | 0.48 | 0.509960159363 | 0.444915254237 | 0.551330798479 | +------+------+----------------+----------------+----------------+ | G(1) | 0.52 | 0.490039840637 | 0.555084745763 | 0.448669201521 | +------+------+----------------+----------------+----------------+ CPD of I: +------+-------+ | I(0) | 0.486 | +------+-------+ | I(1) | 0.514 | +------+-------+ CPD of L: +------+----------------+----------------+ | G | G(0) | G(1) | +------+----------------+----------------+ | L(0) | 0.489959839357 | 0.501992031873 | +------+----------------+----------------+ | L(1) | 0.510040160643 | 0.498007968127 | +------+----------------+----------------+ CPD of S: +------+----------------+----------------+ | I | I(0) | I(1) | +------+----------------+----------------+ | S(0) | 0.512345679012 | 0.468871595331 | +------+----------------+----------------+ | S(1) | 0.487654320988 | 0.531128404669 | +------+----------------+----------------+
参数学习:
pseudo_counts = {'D': [300, 700], 'I': [500, 500], 'G': [800, 200], 'L': [500, 500], 'S': [400, 600]}
model.fit(data, estimator=BayesianEstimator, prior_type='dirichlet', pseudo_counts=pseudo_counts)
for cpd in model.get_cpds():
print("CPD of {variable}:".format(variable=cpd.variable))
print(cpd)
结果如下:
CPD of D: +------+--------+ | D(0) | 0.4005 | +------+--------+ | D(1) | 0.5995 | +------+--------+ CPD of G: +------+-------+----------------+----------------+----------------+ | D | D(0) | D(0) | D(1) | D(1) | +------+-------+----------------+----------------+----------------+ | I | I(0) | I(1) | I(0) | I(1) | +------+-------+----------------+----------------+----------------+ | G(0) | 0.736 | 0.741806554756 | 0.732200647249 | 0.748218527316 | +------+-------+----------------+----------------+----------------+ | G(1) | 0.264 | 0.258193445244 | 0.267799352751 | 0.251781472684 | +------+-------+----------------+----------------+----------------+ CPD of I: +------+-------+ | I(0) | 0.493 | +------+-------+ | I(1) | 0.507 | +------+-------+ CPD of L: +------+----------------+----------------+ | G | G(0) | G(1) | +------+----------------+----------------+ | L(0) | 0.496662216288 | 0.500665778961 | +------+----------------+----------------+ | L(1) | 0.503337783712 | 0.499334221039 | +------+----------------+----------------+ CPD of S: +------+----------------+----------------+ | I | I(0) | I(1) | +------+----------------+----------------+ | S(0) | 0.436742934051 | 0.423381770145 | +------+----------------+----------------+ | S(1) | 0.563257065949 | 0.576618229855 | +------+----------------+----------------+




 浙公网安备 33010602011771号
浙公网安备 33010602011771号