贝叶斯网络——pgmpy 教程
基于pgmpy的贝叶斯推理流程大白话解释
pgmpy是github上的一个开源项目，在网站上他的简介只有很简单的一句话——pgmpy is a python library for working with Probabilistic Graphical Models.
用咱大俗话，它就是一个python库可以推理“概率图”模型，那什么是概率图呢？很简单请看下图：
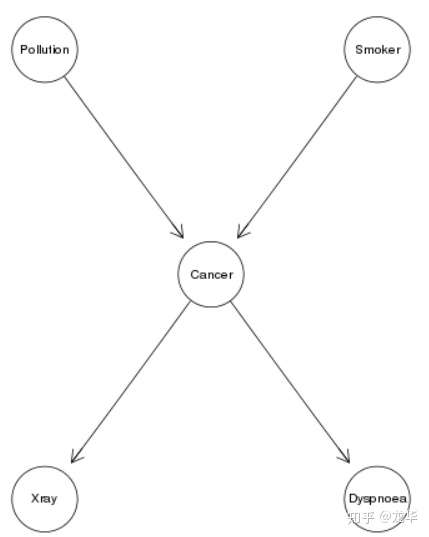cancer model
这是一个很经典的图，我们叫他用于诊断癌症的“贝叶斯模型”，别管他叫啥了，回到我们原来的问题——什么是概率图，上面这个图还不能称为概率图为什么呢？很明显，缺少概率啊。那有同学说了，“你的概率跑哪去了？”。
别急啊，baby! 加上就是了，问题是该怎么加呢，我们可以以常识去思考，上面这个图呢，中间这个圆圈是癌症，周围四个圆圈分别是空气污染、吸烟、x射线、呼吸障碍。再看圆圈之间的箭头，我们是不是可以有个简单的因果关系：某人得癌症的几率，是不是受空气污染、吸烟的影响，同时得了癌症的人，也会导致其受到x射线辐射治疗，以及呈现呼吸障碍的症状啊。
这样通过以上的因果分析，概率就明了啦，我们就可以去添加概率了，首先每个圆圈，我们再学术一点就称为“节点”吧，对于每个节点，我们不考虑他们之间的关联，仅在一个人群里面去观察，人群中有多少人到了癌症，多少人没得，这是不是有个得癌症的概率呢，学术一点，我们称为“先验概率”，同理其他的每个节点的先验概率，我们都可以通过这种思想得到。
如果我们继续观察患癌人群，那么该人群中有呼吸障碍症状的人的概率，我们是不是就知道了，得有同学说了——这也是“先验概率”吗？哈哈，当然不是，就看我的表述，是不是比前面的那个得到癌症概率的表述多了一个条件呢，我这里可是加了一个前提——患癌人群中有呼吸症状的人的概率，所以我们称之为"条件概率"。
我们再回到开始"概率图"这个问题，这个概率到底指的是"先验概率"还是“条件概率”呢，不科学的讲，指的是条件概率，具体为啥说“不科学呢”，那是因为对于最上面的节点来说，没有别的节点指向他们，那这个时候他们的先验概率也是概率图中的概率了。
到现在为止我们介绍完概率图了，核心来了，啥叫人工智能啊。这就要对应我们文章开头说到的推理了，所谓的推理，在这里我们称为贝叶斯推理，有了前面的贝叶斯模型，再进行贝叶斯推理当然是水到渠成的事了，贝叶斯推理的目标是是什么呢，目标还是"概率"。说到这，可能有同学懵逼了，咋还是概率啊？哈哈，这也没办法，贝叶斯推理的核心也就是任何事情都是不确定性的表达，这中间还夹杂着传统的频率学派与贝叶斯学派的争论，在这里我们不做深入的探讨，有兴趣的同学可以自行百度。
回到我们的正题，前面说到我们贝叶斯推理的目的还是个“概率”，那这个概率是什么呢？先说称呼，学术上称为“后验概率”。举个例子，我们有大量的数据表明：一个人患癌症与吸烟呈现明显的关系，甚至我们已经得到两者之间的条件概率，这时候呢，来了一个患者，他有吸烟的习惯还有点轻微的呼吸障碍的症状，那我们想确定他患癌症的概率是多少？这个概率就是我们所求的“后验概率”，而他抽烟的习惯以及呼吸障碍的症状，都是我们事先掌握的”证据信息”，这个证据信息将在推理过程中起到关键作用，也是能得到我们该病人患癌症概率的关键。
下面我们用代码展示了从建模到添加概率再到最终推理的实现过程，短短几行代码，就让你学会应用人工智能的贝叶斯推理技术，是不是很炫酷呢~~
## step1 定义模型结构
from pgmpy.models import BayesianModel
cancer_model = BayesianModel([('Pollution', 'Cancer'),
('Smoker', 'Cancer'),
('Cancer', 'Xray'),
('Cancer', 'Dyspnoea')])
##step2 添加概率
from pgmpy.factors.discrete import TabularCPD
cpd_poll = TabularCPD(variable='Pollution', variable_card=2,
values=[[0.9], [0.1]])
cpd_smoke = TabularCPD(variable='Smoker', variable_card=2,
values=[[0.3], [0.7]])
cpd_cancer = TabularCPD(variable='Cancer', variable_card=2,
values=[[0.03, 0.05, 0.001, 0.02],
[0.97, 0.95, 0.999, 0.98]],
evidence=['Smoker', 'Pollution'],
evidence_card=[2, 2])
cpd_xray = TabularCPD(variable='Xray', variable_card=2,
values=[[0.9, 0.2], [0.1, 0.8]],
evidence=['Cancer'], evidence_card=[2])
cpd_dysp = TabularCPD(variable='Dyspnoea', variable_card=2,
values=[[0.65, 0.3], [0.35, 0.7]],
evidence=['Cancer'], evidence_card=[2])
cancer_model.add_cpds(cpd_poll, cpd_smoke, cpd_cancer, cpd_xray, cpd_dysp)
##step3 进行推理
from pgmpy.inference import VariableElimination
cancer_infer = VariableElimination(cancer_model)
q = asia_infer.query(variables=['cancer'], evidence={'smoke': 'yes'})
print(q)pgmpy 教程
Table of Contents
创建贝叶斯网
在 pgmpy 中, 定义一个贝叶斯网的流程一般是先建立网络结构, 然后填入相关参数.
建立网络结构
from pgmpy.models import BayesianModel
cancer_model = BayesianModel([('Pollution', 'Cancer'),
('Smoker', 'Cancer'),
('Cancer', 'Xray'),
('Cancer', 'Dyspnoea')])
这个网络中有五个节点: Pollution, Cancer, Smoker, Xray, Dyspnoea.
('Pollution', 'Cancer'): 一条有向边, 从 Pollution 指向 Cancer, 表示环境污染有可能导致癌症.
('Smoker', 'Cancer'): 吸烟有可能导致癌症.
('Cancer', 'Xray'): 得癌症的人可能会去照X射线.
('Cancer', 'Dyspnoea'): 得癌症的人可能会呼吸困难.
填入参数
from pgmpy.factors.discrete import TabularCPD
cpd_poll = TabularCPD(variable='Pollution', variable_card=2,
values=[[0.9], [0.1]])
cpd_smoke = TabularCPD(variable='Smoker', variable_card=2,
values=[[0.3], [0.7]])
cpd_cancer = TabularCPD(variable='Cancer', variable_card=2,
values=[[0.03, 0.05, 0.001, 0.02],
[0.97, 0.95, 0.999, 0.98]],
evidence=['Smoker', 'Pollution'],
evidence_card=[2, 2])
cpd_xray = TabularCPD(variable='Xray', variable_card=2,
values=[[0.9, 0.2], [0.1, 0.8]],
evidence=['Cancer'], evidence_card=[2])
cpd_dysp = TabularCPD(variable='Dyspnoea', variable_card=2,
values=[[0.65, 0.3], [0.35, 0.7]],
evidence=['Cancer'], evidence_card=[2])
这些代码, 主要是建立一些概率表, 然后往表里面填入了一些参数.
Pollution: 有两种概率, 分别是 0.9 和 0.1.
Smoker: 有两种概率, 分别是 0.3 和 0.7. (意思是在一个人群里, 有 30% 的人吸烟, 有 70% 的人不吸烟)
Cancer: envidence 表示有 Smoker 和 Pollution 两个节点指向 Cancer 节点;
[0.03, 0.05, 0.001, 0.02] 的意思, 通过下表可以较容易看出来:
| Pollution | Pollution_0 | Pollution_0 | Pollution_1 | Pollution_1 |
|---|---|---|---|---|
| Smoker | Smoker_0 | Smoker_1 | Smoker_0 | Smoker_1 |
| Cancer_0 | 0.03 | 0.05 | 0.001 | 0.02 |
| Cancer_1 | 0.97 | 0.95 | 0.999 | 0.98 |
可以看出, 环境不好, 又抽烟的人, 有 0.98 的概率得癌症.
Xray: 通过 envidence 可以看出, 只有 Cancer 指向它; [0.9, 0.2] 表示, 未得癌症的人去照X光, 有 0.9 的概率正常, 而得了癌症的人去照X光, 有 0.2 的概率正常, [0.1, 0.8] 表示, 未得癌症的人去照X光, 有 0.1 的概率不正常, 而得癌症的人有 0.8 的概率不正常.
Dyspnoea: 未得癌症的人有 0.65 的可能性呼吸正常, 得癌症的人只有 0.3 的可能性呼吸正常; 未得癌症的人有 0.35 的可能性呼吸困难, 得癌症的人有 0.7 的可能性呼吸困难.
将数据加入网络
# Associating the parameters with the model structure. cancer_model.add_cpds(cpd_poll, cpd_smoke, cpd_cancer, cpd_xray, cpd_dysp) # Checking if the cpds are valid for the model. cancer_model.check_model()
第一行代码表示将概率分布表加入网络中; 第二行代码验证模型数据的正确性(至于怎么验证的, 我没有看源码, 但是猜测是验证相关数据的和是否为1, 验证数据中是否有负数, 等等).
相关的检查
cancer_model.is_active_trail('Pollution', 'Smoker') # False
cancer_model.is_active_trail('Pollution', 'Smoker', observed=['Cancer']) # True
cancer_model.local_independencies('Xray') # (Xray _|_ Dyspnoea, Smoker, Pollution | Cancer)
cancer_model.get_independencies()
第一行代码表示, Pollution 节点是否指向 Smoker 节点, 返回的是 False.
第二行代码表示, Cancer 节点的计算, 是否与 Pollution 和 Smoker 两个节点有关, 返回的是 True.
第三行代码的输出表示, Xray 与 Dyspnoea, Smoker, Pollution 不相关, 与 Cancer 相关.
第四行代码输出所有的依赖关系.
使用 Asia 网络进行推理
在构建了贝叶斯网之后, 我们使用贝叶斯网来进行推理. 推理算法分精确推理和近似推理. 精确推理有变量消元法和团树传播法; 近似推理算法是基于随机抽样的算法.
Asia 网络是早期贝叶斯网文献中给出的一个网络, 与肺结核, 肺癌, 支气管炎等有关, 和我们之前的那个网络很相似. 我们使用 Asia 网络来看一下如何进行推理.
创建源文件 asia.py
下载网络模型放到源文件目录下:
wget http://www.bnlearn.com/bnrepository/asia/asia.bif.gz gzip -qd asia.bif.gz
编辑 asia.py:
导入 Asia 网络:
from pgmpy.readwrite import BIFReader
reader = BIFReader('asia.bif')
asia_model = reader.get_model()
输出节点信息:
print(asia_model.nodes()) # ['xray', 'bronc', 'asia', 'dysp', 'lung', 'either', 'smoke', 'tub']
输出依赖关系:
print(asia_model.edges())
结果如下:
[('bronc', 'dysp'),
('asia', 'tub'),
('lung', 'either'),
('either', 'dysp'),
('either', 'xray'),
('smoke', 'bronc'),
('smoke', 'lung'),
('tub', 'either')]
查看概率分布:
print(asia_model.get_cpds())
结果如下:
[<TabularCPD representing P(asia:2) at 0x7f92cf1e46d0>, <TabularCPD representing P(bronc:2 | smoke:2) at 0x7f92ea70f990>, <TabularCPD representing P(dysp:2 | bronc:2, either:2) at 0x7f92f80f4ed0>, <TabularCPD representing P(either:2 | lung:2, tub:2) at 0x7f92e8e71dd0>, <TabularCPD representing P(lung:2 | smoke:2) at 0x7f92cf1e4c50>, <TabularCPD representing P(smoke:2) at 0x7f92cf1e4ed0>, <TabularCPD representing P(tub:2 | asia:2) at 0x7f92cf1ec210>, <TabularCPD representing P(xray:2 | either:2) at 0x7f92cf1ec410>]
直观显示某节点的概率分布:
print(asia_model.get_cpds('xray').values)
结果如下:
[[0.98 0.05] [0.02 0.95]]
变量消除法
变量消除法是精确推断的一种方法.
from pgmpy.inference import VariableElimination
asia_infer = VariableElimination(asia_model)
q = asia_infer.query(variables=['bronc'], evidence={'smoke': 0})
print(q['bronc'])
结果如下:
+---------+--------------+ | bronc | phi(bronc) | |---------+--------------| | bronc_0 | 0.6000 | | bronc_1 | 0.4000 | +---------+--------------+
意思是, 在不吸烟的情况下, 得支气管炎的概率是 0.4, 未得支气管炎的概率是 0.6.
在在吸烟情况下, 得支气管炎的概率和未得支气管炎的概率可以这样查询:
q = asia_infer.query(variables=['bronc'], evidence={'smoke': 1})
print(q['bronc'])
结果如下:
+---------+--------------+ | bronc | phi(bronc) | |---------+--------------| | bronc_0 | 0.3000 | | bronc_1 | 0.7000 | +---------+--------------+
利用训练数据学习
场景: 投硬币, 训练数据中, 有 30% 的正面朝上, 有 70% 的反面朝上. 我们使用极大似然估计和狄利克雷分布下贝叶斯参数先验估计硬币的条件概率分布.
生成数据:
import numpy as np import pandas as pd raw_data = np.array([0] * 30 + [1] * 70) data = pd.DataFrame(raw_data, columns=['coin'])
定义贝叶斯网:
from pgmpy.models import BayesianModel
from pgmpy.estimators import MaximumLikelihoodEstimator, BayesianEstimator
model = BayesianModel()
model.add_node('coin')
使用极大似然估计:
model.fit(data, estimator=MaximumLikelihoodEstimator)
print(model.get_cpds('coin'))
结果如下:
+---------+-----+ | coin(0) | 0.3 | +---------+-----+ | coin(1) | 0.7 | +---------+-----+
使用狄利克雷分布作为先验分布的贝叶斯推论:
model.fit(data, estimator=BayesianEstimator, prior_type='dirichlet', pseudo_counts={'coin': [50, 50]})
print(model.get_cpds('coin'))
结果如下:
+---------+-----+ | coin(0) | 0.4 | +---------+-----+ | coin(1) | 0.6 | +---------+-----+
更复杂的例子(学生例子)
学生例子中包含5个随机变量, 如下所示:
| 变量 | 含义 | 取值 |
|---|---|---|
| Difficulty | 课程本身难度 | 0=easy, 1=difficult |
| Intelligence | 学生聪明程度 | 0=stupid, 1=smart |
| Grade | 学生课程成绩 | 1=A, 2=B, 3=C |
| SAT | 学生高考成绩 | 0=low, 1=high |
| Letter | 可否获得推荐信 | 0=未获得, 1=获得 |
生成数据:
import numpy as np import pandas as pd raw_data = np.random.randint(low=0, high=2, size=(1000, 5)) data = pd.DataFrame(raw_data, columns=['D', 'I', 'G', 'L', 'S'])
定义模型:
from pgmpy.models import BayesianModel
from pgmpy.estimators import MaximumLikelihoodEstimator, BayesianEstimator
model = BayesianModel([('D', 'G'), ('I', 'G'), ('I', 'S'), ('G', 'L')])
model.fit(data, estimator=MaximumLikelihoodEstimator)
for cpd in model.get_cpds():
print("CPD of {variable}:".format(variable=cpd.variable))
print(cpd)
结果如下:
CPD of D: +------+-------+ | D(0) | 0.501 | +------+-------+ | D(1) | 0.499 | +------+-------+ CPD of G: +------+------+----------------+----------------+----------------+ | D | D(0) | D(0) | D(1) | D(1) | +------+------+----------------+----------------+----------------+ | I | I(0) | I(1) | I(0) | I(1) | +------+------+----------------+----------------+----------------+ | G(0) | 0.48 | 0.509960159363 | 0.444915254237 | 0.551330798479 | +------+------+----------------+----------------+----------------+ | G(1) | 0.52 | 0.490039840637 | 0.555084745763 | 0.448669201521 | +------+------+----------------+----------------+----------------+ CPD of I: +------+-------+ | I(0) | 0.486 | +------+-------+ | I(1) | 0.514 | +------+-------+ CPD of L: +------+----------------+----------------+ | G | G(0) | G(1) | +------+----------------+----------------+ | L(0) | 0.489959839357 | 0.501992031873 | +------+----------------+----------------+ | L(1) | 0.510040160643 | 0.498007968127 | +------+----------------+----------------+ CPD of S: +------+----------------+----------------+ | I | I(0) | I(1) | +------+----------------+----------------+ | S(0) | 0.512345679012 | 0.468871595331 | +------+----------------+----------------+ | S(1) | 0.487654320988 | 0.531128404669 | +------+----------------+----------------+
参数学习:
pseudo_counts = {'D': [300, 700], 'I': [500, 500], 'G': [800, 200], 'L': [500, 500], 'S': [400, 600]}
model.fit(data, estimator=BayesianEstimator, prior_type='dirichlet', pseudo_counts=pseudo_counts)
for cpd in model.get_cpds():
print("CPD of {variable}:".format(variable=cpd.variable))
print(cpd)
结果如下:
CPD of D: +------+--------+ | D(0) | 0.4005 | +------+--------+ | D(1) | 0.5995 | +------+--------+ CPD of G: +------+-------+----------------+----------------+----------------+ | D | D(0) | D(0) | D(1) | D(1) | +------+-------+----------------+----------------+----------------+ | I | I(0) | I(1) | I(0) | I(1) | +------+-------+----------------+----------------+----------------+ | G(0) | 0.736 | 0.741806554756 | 0.732200647249 | 0.748218527316 | +------+-------+----------------+----------------+----------------+ | G(1) | 0.264 | 0.258193445244 | 0.267799352751 | 0.251781472684 | +------+-------+----------------+----------------+----------------+ CPD of I: +------+-------+ | I(0) | 0.493 | +------+-------+ | I(1) | 0.507 | +------+-------+ CPD of L: +------+----------------+----------------+ | G | G(0) | G(1) | +------+----------------+----------------+ | L(0) | 0.496662216288 | 0.500665778961 | +------+----------------+----------------+ | L(1) | 0.503337783712 | 0.499334221039 | +------+----------------+----------------+ CPD of S: +------+----------------+----------------+ | I | I(0) | I(1) | +------+----------------+----------------+ | S(0) | 0.436742934051 | 0.423381770145 | +------+----------------+----------------+ | S(1) | 0.563257065949 | 0.576618229855 | +------+----------------+----------------+
