贝叶斯网络python实战（以泰坦尼克号数据集为例，pgmpy库）

贝叶斯网络python实战（以泰坦尼克号数据集为例，pgmpy库）

leida_wt 2019-03-24 23:05:36  16815  收藏 140

分类专栏： 机器学习 文章标签： pgmpy 贝叶斯网络 泰坦尼克 机器学习 图网络

版权

 

文章目录

• • 贝叶斯网络简介
  • • • 贝叶斯推断思路
      • 贝叶斯网络
  • 贝叶斯网络的实现
  • • • 应用步骤
      • 泰坦尼克数据集背景介绍
      • 模型结构搭建
      • 模型参数构建
      • • 贝叶斯估计器
      • 推理
      • 自动设计网络结构->使用结构学习方法
      • 模型保存
  • 先验
  • 练手数据集
  • • • Binary Classification
      • Multiclass Classification
  • 下载

本文的相关数据集，代码见文末百度云

 

贝叶斯网络简介

贝叶斯网络是一种置信网络，一个生成模型。（判别模型，生成模型的区分可以这样：回答p(label|x)即样本x属于某一类别的可能的，就是判别模型，而回答p(x,label) 和p(x|label)的，即回答在给定的类别中找样本x及样本分布情况的，即为生成模型。生成模型给出的联合分布比判别网络能给出更多的信息，对其求边缘分布即可得p(label|x) p(x|label)）同时贝叶斯网络还是一个简单的白盒网络，提供了高可解释性的可能。相比于大热的几乎无所不能的深度神经网络，贝叶斯网络仍有他的优势和应用场景。比如在故障分析，疾病诊断里，我们不仅需要回答是不是，更重要的是回答为什么，并给出依据。这样的场景下，以贝叶斯网络为代表的一些可解释好的白盒网络更加有优势。

贝叶斯推断思路

与频率派直接从数据统计分析构建模型不同，贝叶斯派引入一个先验概率，表达对事件的已有了解，然后利用观测数据对先验知识进行修正，如通常把抛硬币向上的概率认为是0.5，这是个很朴素的先验知识，若是实验结果抛出了500-500的结果，那么证明先验知识是可靠的，合适的，若是出现100-900结果，那么先验知识会被逐渐修改（越来越相信这是个作弊硬币），当实验数据足够多的时候，先验知识就几乎不再体现，这时候得到与频率派几乎相同的结果。如图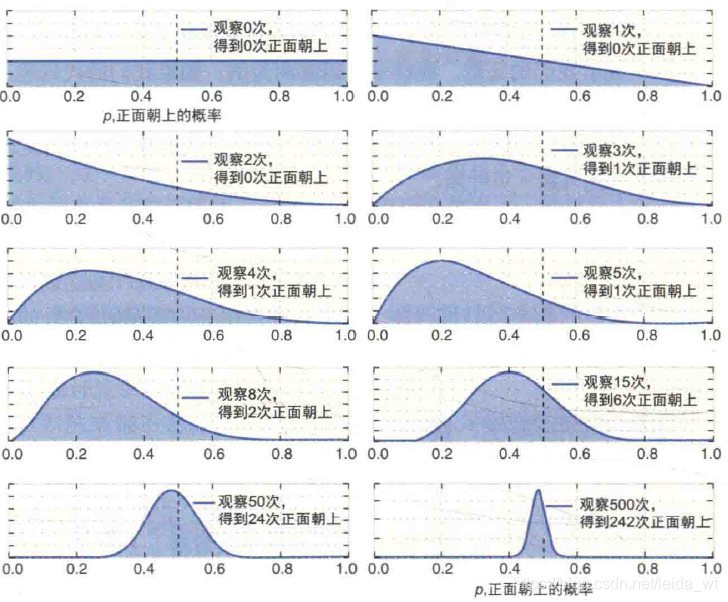

具体例子推导可见here

贝叶斯网络

贝叶斯网络结构如下所示，其是有特征节点和链接构成的有向无环图。节点上是概率P(A),P(B)… 连接上是条件概率P(A|B) P(A|C) … 即若有A指向B的连接，则连接代表的就应为P(B|A)，更多信息可参考以下内容，这里不再赘述，贝叶斯网络结构本身不困难，其难点主要在于推理算法等数值计算问题，如为应用则无需深究。
贝叶斯网络发展及其应用综述
《贝叶斯网络引论》@张连文
静态贝叶斯网络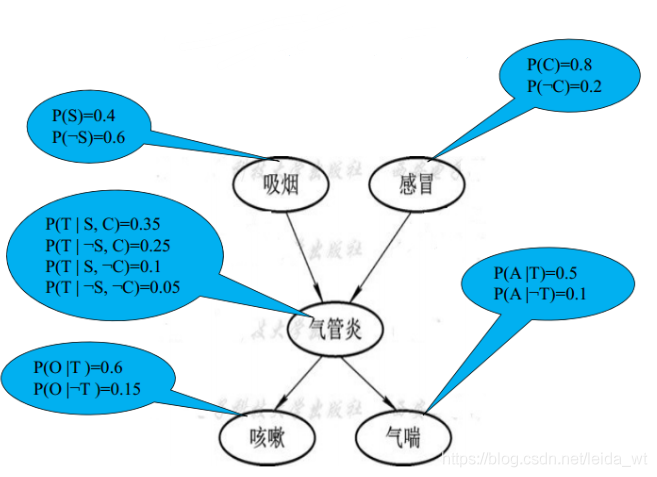

贝叶斯网络的实现

相关工具一直很丰富，matlab，R上都有成熟的工具。这里使用了python下的pgmpy，轻量好用，不像pymc那样容易安装困难。
安装：
conda install -c ankurankan pgmpy
或
pip install pgmpy

应用步骤

1.先确定以那些变量（特征）为节点，这里还包括由特征工程特征选择之类的工作。当然若有专业知识的参与会得到更合理的特征选择。
2.确定网络结构（拓扑）用以反应变量节点之间的依赖关系。也就是明确图的结构。这里既可以在有专家参与的情况下手工设计，也可以自动找到高效合适的网络，称为结构学习。贝叶斯网络的结构对最终网络性能很关键，若是构建所谓全连接贝叶斯网（即各个变量间两两相连），虽没有遗漏关联，但会导致严重的过拟合，因为数据量很难支撑起全连接直接海量的条件概率。
3.明确每条边上的条件概率。和结构一样，参数也可由专家手工确定（先验），亦可通过数据自动学习（即参数学习），或两者同时进行。
下面以一个经典数据集为例展示如何利用pgmpy包进行贝叶斯网络建模

泰坦尼克数据集背景介绍

ref:https://www.jianshu.com/p/9b6ee1fb7a60
https://www.kaggle.com/c/titanic
这是kaggle经典数据集，主要是让参赛选手根据训练集中的乘客数据和存活情况进行建模，进而使用模型预测测试集中的乘客是否会存活。乘客特征总共有11个，以下列出。这个数据集特征明确，数据量不大，很适合应用贝叶斯网络之类的模型来做，目前最好的结果是正确率应该有80+%（具体多少因为答案泄露不好讲了）

PassengerId => 乘客ID
Pclass => 客舱等级(1/2/3等舱位)
Name => 乘客姓名
Sex => 性别
Age => 年龄
SibSp => 兄弟姐妹数/配偶数
Parch => 父母数/子女数
Ticket => 船票编号
Fare => 船票价格
Cabin => 客舱号
Embarked => 登船港口
在开始建模之前，先进行下特征工程，处理原始数据集的缺项等。这里前面处理主要采用https://www.jianshu.com/p/9b6ee1fb7a60的方法（他应用pandas清理数据的技巧很值得一学），我在他的处理后，进一步进行了一些离散化处理，以使得数据符合贝叶斯网络的要求（贝叶斯网络也有支持连续变量的版本，但因为推理，学习的困难，目前还用的很少），最后保留5个特征。

'''
PassengerId => 乘客ID
Pclass => 客舱等级(1/2/3等舱位)
Name => 乘客姓名
Sex => 性别 清洗成male=1 female=0
Age => 年龄 插补后分0,1,2 代表 幼年（0-15） 成年（15-55） 老年（55-）
SibSp => 兄弟姐妹数/配偶数
Parch => 父母数/子女数
Ticket => 船票编号
Fare => 船票价格 经聚类变0 1 2 代表少 多 很多
Cabin => 客舱号 清洗成有无此项，并发现有的生存率高
Embarked => 登船港口 清洗na,填S
'''
# combine train and test set.
train=pd.read_csv('./train.csv')
test=pd.read_csv('./test.csv')
full=pd.concat([train,test],ignore_index=True)
full['Embarked'].fillna('S',inplace=True)
full.Fare.fillna(full[full.Pclass==3]['Fare'].median(),inplace=True)
full.loc[full.Cabin.notnull(),'Cabin']=1
full.loc[full.Cabin.isnull(),'Cabin']=0
full.loc[full['Sex']=='male','Sex']=1
full.loc[full['Sex']=='female','Sex']=0

full['Title']=full['Name'].apply(lambda x: x.split(',')[1].split('.')[0].strip())
nn={'Capt':'Rareman', 'Col':'Rareman','Don':'Rareman','Dona':'Rarewoman',
    'Dr':'Rareman','Jonkheer':'Rareman','Lady':'Rarewoman','Major':'Rareman',
    'Master':'Master','Miss':'Miss','Mlle':'Rarewoman','Mme':'Rarewoman',
    'Mr':'Mr','Mrs':'Mrs','Ms':'Rarewoman','Rev':'Mr','Sir':'Rareman',
    'the Countess':'Rarewoman'}
full.Title=full.Title.map(nn)
# assign the female 'Dr' to 'Rarewoman'
full.loc[full.PassengerId==797,'Title']='Rarewoman'
full.Age.fillna(999,inplace=True)
def girl(aa):
    if (aa.Age!=999)&(aa.Title=='Miss')&(aa.Age<=14):
        return 'Girl'
    elif (aa.Age==999)&(aa.Title=='Miss')&(aa.Parch!=0):
        return 'Girl'
    else:
        return aa.Title

full['Title']=full.apply(girl,axis=1)

Tit=['Mr','Miss','Mrs','Master','Girl','Rareman','Rarewoman']
for i in Tit:
    full.loc[(full.Age==999)&(full.Title==i),'Age']=full.loc[full.Title==i,'Age'].median()
    
full.loc[full['Age']<=15,'Age']=0
full.loc[(full['Age']>15)&(full['Age']<55),'Age']=1
full.loc[full['Age']>=55,'Age']=2
full['Pclass']=full['Pclass']-1
from sklearn.cluster import KMeans
Fare=full['Fare'].values
Fare=Fare.reshape(-1,1)
km = KMeans(n_clusters=3).fit(Fare)   #将数据集分为2类
Fare = km.fit_predict(Fare)
full['Fare']=Fare
full['Fare']=full['Fare'].astype(int)
full['Age']=full['Age'].astype(int)
full['Cabin']=full['Cabin'].astype(int)
full['Pclass']=full['Pclass'].astype(int)
full['Sex']=full['Sex'].astype(int)
#full['Survived']=full['Survived'].astype(int)


dataset=full.drop(columns=['Embarked','Name','Parch','PassengerId','SibSp','Ticket','Title'])
dataset.dropna(inplace=True)
dataset['Survived']=dataset['Survived'].astype(int)
#dataset=pd.concat([dataset, pd.DataFrame(columns=['Pri'])])
train=dataset[:800]
test=dataset[800:]
'''
最后保留如下项目,并切出800的训练集：
Pclass => 客舱等级(0/1/2等舱位)
Sex => 性别 male=1 female=0
Age => 年龄 插补后分0,1,2 代表 幼年（0-15） 成年（15-55） 老年（55-）
Fare => 船票价格 经聚类变0 1 2 代表少 多 很多
Cabin => 客舱号 清洗成有无此项，并发现有的生存率高
'''

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79
• 80

模型结构搭建

这里先手动设计网络结构。
凭借对数据的理解，先设计如下的结构

from pgmpy.models import BayesianModel
from pgmpy.estimators import BayesianEstimator

#model = BayesianModel([('Age', 'Pri'), ('Sex', 'Pri'),('Pri','Survived'),('Fare','Pclass'),('Pclass','Survived'),('Cabin','Survived')])
model = BayesianModel([('Age', 'Survived'), ('Sex', 'Survived'),('Fare','Pclass'),('Pclass','Survived'),('Cabin','Survived')])

• 1
• 2
• 3
• 4
• 5

其中(‘Age’, ‘Survived’)表示Age指向Survived

pgmpy没有提供可视化，这里简单用graphviz实现了一下。

def showBN(model，save=False):
    '''传入BayesianModel对象，调用graphviz绘制结构图，jupyter中可直接显示'''
    from graphviz import Digraph
    node_attr = dict(
     style='filled',
     shape='box',
     align='left',
     fontsize='12',
     ranksep='0.1',
     height='0.2'
    )
    dot = Digraph(node_attr=node_attr, graph_attr=dict(size="12,12"))
    seen = set()
    edges=model.edges()
    for a,b in edges:
        dot.edge(a,b)
    if save:
        dot.view(cleanup=True)
    return dot
showBN(model)    

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20

模型参数构建

接下来就是确定网络的参数，也就是各个边上的条件概率。
若手工填入，可这样写

from pgmpy.factors.discrete import TabularCPD
#构建cpd表
my_cpd= TabularCPD(variable='Pclass', variable_card=3,
                      values=[[0.65, 0.3], [0.30, 0.6],[0.05,0.1]],
                      evidence=['Fare'], evidence_card=[2])
# 填cpd表
model.add_cpds(my_cpd)

# 执行检查（可选，用于检查cpd是否填错）
cancer_model.check_model()                 

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

但在此例子里，使用参数学习的办法从数据里自动学习。
参数学习有两种典型方法，极大似然估计和贝叶斯估计。因为前者的过拟合严重，一般都使用后者进行参数学习。pgmpy提供的贝叶斯估计器提供三种先验分布的支持，‘dirichlet’, ‘BDeu’, ‘K2’，实际上都是dirichlet分布，这里解释下贝叶斯估计器的工作原理。

贝叶斯估计器

在贝叶斯分析的框架下，待求参数θ被看做是随机变量，对他的估计就是在其先验上，用数据求后验，因此先要有对θ的先验假设。而我们通常取的先验分布就是dirichlet（狄利克雷）分布。对于一个含有i个离散状态的节点，我们设其参数为
并令其先验为狄利克雷分布D[α1，α2…αi]（i=2时也称beta分布）

这个先验有i个参数，数学上证明了，这些参数就相当于将先验表达成了α个虚拟样本，其中满足X=xi的样本数为αi，这个α就成为等价样本量（equivalent_sample_size）。这个巧合其实正式先验函数取这个函数的缘由，另外，其计算后的后验分布也是狄利克雷分布（称这种行为叫共轭先验）。注：各个分布可参考 https://zhuanlan.zhihu.com/p/37976562
至此可以理解pgmpy提供的贝叶斯估计器的参数的含义了。
其定义为estimate_cpd(node, prior_type=‘BDeu’, pseudo_counts=[], equivalent_sample_size=5)
node是节点名
当prior_type=‘BDeu’ 就表示选择了一个equivalent_sample_size=5的无差别客观先验，认定各个概率相等，不提供信息，但并不是没用，这个先验起到了类似神经网络里头控制过拟合的正则项的作用。
当prior_type='dirichlet’表示选择一般的狄利克雷分布，这时候要主动填入[α1，α2…αi]
当prior_type= ‘K2’ 意为 ‘dirichlet’ + setting every pseudo_count to 1
具体使用如下：

data = pd.DataFrame(data={'A': [0, 0, 1], 'B': [0, 1, 0], 'C': [1, 1, 0]})
model = BayesianModel([('A', 'C'), ('B', 'C')])
estimator = BayesianEstimator(model, data)
cpd_C = estimator.estimate_cpd('C', prior_type="dirichlet", pseudo_counts=[1, 2])
model.add_cpds(cpd_C)

• 1
• 2
• 3
• 4
• 5
• 6

上面是一个一个填进去的，在本例中有更简单的方法，就是利用提供的fit函数，一并估计各个cpd（条件概率），即

model.fit(train, estimator=BayesianEstimator, prior_type="BDeu") # default equivalent_sample_size=5

• 1

直接把前面处理得到dataframe 传入即可。这里记录一个bug：pgmpy目前将离散变量命名限制为从0开始，所以本例子里的Pclass 项从（1/2/3等级）都减一处理成了（0/1/2等级）以解决此问题。
dirichlet也可在fit函数里使用，只要传入pseudo_counts字典即可，如下面这样

pseudo_counts = {'D': [300, 700], 'I': [500, 500], 'G': [800, 200], 'L': [500, 500], 'S': [400, 600]}
model.fit(data, estimator=BayesianEstimator, prior_type='dirichlet', pseudo_counts=pseudo_counts)

• 1
• 2

到此为止，模型已经完全构建完毕，下面可以开始使用其进行推理了。

推理

首先可以通过一些方法查看模型

#输出节点信息
print(model.nodes())
#输出依赖关系
print(model.edges())
#查看某节点概率分布
print(model.get_cpds('Pclass').values)

• 1
• 2
• 3
• 4
• 5
• 6

当然我们更关心的是给定某些节点后，感兴趣节点的概率等，这就是推理。
贝叶斯网络推理分成：
1.后验概率问题：
表达为求P（Q|E=e） 其中Q为查询变量 E为证据变量
即如本例子里已知一个人，女，<15岁，高票价，问生还几率是多少？
2.最大后验假设问题（MAP）：

已知证据E时，对某些变量的转态组合感兴趣（称假设变量H），找最可能组合就是最大后验假设问题。如本例子里，问一个活下来的女乘客最可能有是什么舱段，年龄？
3.最大可能解释问题（MPE）：是2的特例，即假设包含网络里所有非证据变量（同时也可包含证据变量）

贝叶斯网络推理主要有两类方法，精确推理（变量化简Variable Elination和置信传播）和近似推理(如mcmc采样)，一般精确推理足以解决
pgmpy解决1可以用query函数 解决2，3可以用map_query函数
通过这些查询可以获得我们感兴趣的关于因果关系信息，这是贝叶斯网络模型的一大优势。此处的因果关系并不可以解释为一般意义上的逻辑因果，而是表示一种概率上的相关，比如我们不能将P(天亮了|公鸡打鸣)很高解释为是因为公鸡打鸣天才亮的。

from pgmpy.inference import VariableElimination
model_infer = VariableElimination(model)
q = model_infer.query(variables=['Survived'], evidence={'Fare': 0})
print(q['Survived'])
'''
+------------+-----------------+
| Survived   |   phi(Survived) |
+============+=================+
| Survived_0 |          0.6341 |
+------------+-----------------+
| Survived_1 |          0.3659 |
+------------+-----------------+
'''
q = model_infer.map_query(variables=['Fare','Age','Sex','Pclass','Cabin'], evidence={'Survived': 1})
print(q)#{'Sex': 0, 'Fare': 0, 'Age': 1, 'Pclass': 2, 'Cabin': 0}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16

上面的代码使用了VariableElimination方法，亦可用BeliefPropagation，其有相同的接口。

与fit函数类似，也提供了输入dataframe的简便推理方法predict，如下
只要剔除想预测的列输入predict函数，就可以得到预测结果的dataframe

predict_data=test.drop(columns=['Survived'],axis=1)
y_pred = model.predict(predict_data)
print((y_pred['Survived']==test['Survived']).sum()/len(test))
#测试集精度0.8131868131868132

• 1
• 2
• 3
• 4

只是用了泰坦尼克数据集的一部分特征随手设计网络就可以达到不错的效果了，精度81.3%，上传kaggle的正确率0.77990。

自动设计网络结构->使用结构学习方法

ref：
https://github.com/pgmpy/pgmpy_notebook
《贝叶斯网络引论》

自动设计网络结构的核心问题有两个，一个是评价网络好坏的指标，另一个是查找的方法。穷举是不可取的，因为组合数太大，只能是利用各种启发式方法或是限定搜索条件以减少搜索空间，因此产生两大类方法，Score-based Structure Learning与constraint-based structure learning 以及他们的结合hybrid structure learning。
1.Score-based Structure Learning
这个方法依赖于评分函数，常用的有bdeu k2 bic，更合理的网络评分更高，如下面的例子
此例子随机产生x y 并令z=x+y，显然X -> Z <- Y的结构合理

import pandas as pd
import numpy as np
from pgmpy.estimators import BdeuScore, K2Score, BicScore
from pgmpy.models import BayesianModel

# create random data sample with 3 variables, where Z is dependent on X, Y:
data = pd.DataFrame(np.random.randint(0, 4, size=(5000, 2)), columns=list('XY'))
data['Z'] = data['X'] + data['Y']

bdeu = BdeuScore(data, equivalent_sample_size=5)
k2 = K2Score(data)
bic = BicScore(data)

model1 = BayesianModel([('X', 'Z'), ('Y', 'Z')])  # X -> Z <- Y
model2 = BayesianModel([('X', 'Z'), ('X', 'Y')])  # Y <- X -> Z


print(bdeu.score(model1))
print(k2.score(model1))
print(bic.score(model1))

print(bdeu.score(model2))
print(k2.score(model2))
print(bic.score(model2))
'''
-13936.101051153362
-14326.88012027081
-14292.1400887
-20902.744280734016
-20929.567083476162
-20946.7926535
'''

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32

X -> Z <- Y 的评分更高
而依据评分函数进行搜索的搜索方法常用的有穷举（5个节点以下可用）和 爬山算法（一个贪婪算法）pympy的实现如下：

from pgmpy.estimators import HillClimbSearch

# create some data with dependencies
data = pd.DataFrame(np.random.randint(0, 3, size=(2500, 8)), columns=list('ABCDEFGH'))
data['A'] += data['B'] + data['C']
data['H'] = data['G'] - data['A']

hc = HillClimbSearch(data, scoring_method=BicScore(data))
best_model = hc.estimate()
print(best_model.edges())
#[('A', 'C'), ('A', 'B'), ('C', 'B'), ('G', 'A'), ('G', 'H'), ('H', 'A')]

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12

2.Constraint-based Structure Learning
比如根据独立性得到最优结构的方法，相对来讲前一种更有效

from pgmpy.independencies import Independencies

ind = Independencies(['B', 'C'],
                     ['A', ['B', 'C'], 'D'])
ind = ind.closure()  # required (!) for faithfulness

model = ConstraintBasedEstimator.estimate_from_independencies("ABCD", ind)

print(model.edges())
#[('A', 'D'), ('B', 'D'), ('C', 'D')]

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

回到泰坦尼克的例子，使用HillClimbSearch试了以下，在自己的测试集得到了和之前手工设计网络相同的精度（kaggle测试成绩略低一些），但是模型结构更复杂，不过看看给出的模型可以发现一些有趣的东西，比如Cabin Pclass Fare 相关，Age还影响了Sex等等

from pgmpy.estimators import HillClimbSearch
from pgmpy.estimators import BdeuScore, K2Score, BicScore
hc = HillClimbSearch(train, scoring_method=BicScore(train))
best_model = hc.estimate()
#print(best_model.edges())
showBN(best_model)

• 1
• 2
• 3
• 4
• 5
• 6

best_model.fit(train, estimator=BayesianEstimator, prior_type="BDeu") # default equivalent_sample_size=5
predict_data=test.drop(columns=['Survived'],axis=1)
y_pred = best_model.predict(predict_data)
(y_pred['Survived']==test['Survived']).sum()/len(test)#测试集精度
#0.8131868131868132

• 1
• 2
• 3
• 4
• 5

模型保存

略

先验

这里摘录一些下文对先验的介绍
ref:Bayesian Methods for Hackers chp6

贝叶斯先验可以分为两类:客观先验和主观先验。客观先验的目的是让数据对后验影响最大，主观先验的目的是让从业者对前验表达自己的观点。
事实上，从选择先验分布开始就已经开始搭建模型了，属于建模的一部分。如果后验不符合要求，自然可修改更换先验，这是无关紧要的。没有正确的模型，只有有用的模型。
经验贝叶斯方法
一种叫经验贝叶斯方法融合了频率派的做法，采用 数据>先验>数据>后验 的方法，从观测数据的统计特征构建先验分布。这种方法实则违背了贝叶斯推理 先验>数据>后验 的思路。
从专家获得先验分布
可以考虑实验转盘赌法捕获专家认为的先验分布形状。做法是让专家吧固定总数的筹码放在各个区间上以此来表达各个区段的概率，如下所示。之后可用合适的分布对此进行建模拟合，得到专家先验。

判断先验是否合适
只要先验在某处概率不为零，后验就有机会在此处表达任意的概率。当后验分布的概率堆积在先验分布的上下界时，那么很肯先验是不大对的。（比如用Uniform（0,0.5）作为真实值p=0.7的先验，那么后验推断的结果会堆积在0.5一侧，表明真实值极可能大于0.5）

练手数据集

Binary Classification

• Indian Liver Patient Records
• Synthetic Financial Data for Fraud Detection
• Business and Industry Reports
• Can You Predict Product Backorders?
• Exoplanet Hunting in Deep Space
• Adult Census Income

Multiclass Classification

• Iris Species
• Fall Detection Data from China
• Biomechanical Features of Orthopedic Patients

下载

链接: https://pan.baidu.com/s/1Im_Ls_Nul-swY9vrTueViw 提取码: 7isb