LightGBM为什么比xgbost好？——选择梯度大(残差大)样本来进行特征分裂生成的树，借鉴了Adaboost的更改样本权重，错误的分类会更高权重对待

LightGBM

（Light Gradient Boosting Machine）是一款基于决策树算法的分布式梯度提升框架。为了满足工业界缩短模型计算时间的需求，LightGBM的设计思路主要是两点：
减小数据对内存的使用，保证单个机器在不牺牲速度的情况下，尽可能地用上更多的数据；
减小通信的代价，提升多机并行时的效率，实现在计算上的线性加速。
由此可见，LightGBM的设计初衷就是提供一个快速高效、低内存占用、高准确度、支持并行和大规模数据处理的数据科学工具。
LightGBM是微软旗下的Distributed Machine Learning Toolkit （DMKT）的一个项目，由2014年首届阿里巴巴大数据竞赛获胜者之一柯国霖主持开发。虽然其开源时间才仅仅2个月，但是其快速高效的特点已经在数据科学竞赛中崭露头角。Allstate Claims Severity竞赛中的冠军解决方案里就使用了LightGBM，并对其大嘉赞赏。

特性

优化速度与内存使用。
稀疏优化。
优化准确率。使用leaf-wise生长方式，可以处理分类变量。
优化网络通讯。
支持三种模式并行。
（1）特征并行：
a. Workers find local best split point {feature, threshold} on the local feature set.
b. Communicate local best splits with each other and get the best one.
c. Perform the best split.
（2）数据并行：
a. Instead of “Merge global histograms from all local histograms”, LightGBM use “Reduce Scatter” to merge histograms of different (non-overlapping) features for different workers. Then workers find the local best split on local merged histograms and sync up the global best split.
b. As aforementioned, LightGBM uses histogram subtraction to speed up training. Based on this, we can communicate histograms only for one leaf, and get its neighbor’s histograms by subtraction as well.
（3）投票并行：
Voting parallel further reduces the communication cost in data-parallel to constant cost. It uses two-stage voting to reduce the communication cost of feature histograms.

常见问题

LightGBM和XGBoost有什么区别？他们的loss一样么？ 算法层面有什么区别？
答：LightGBM：基于Histogram的决策树算法；Leaf-wise的叶子生长策略；Cache命中率优化；直接支持类别特征（categorical Feature）；XGBoost：预排序；Level-wise的层级生长策略；特征对梯度的访问是一种随机访问。

LightGBM有哪些实现，各有什么区别？
答：gbdt:梯度提升决策树，串行速度慢，容易过拟合；rf：随机森林，并行速度快；dart：训练较慢；goss：容易过拟合。

LigthGBM是boosting集合模型中的新进成员，由微软提供，它和XGBoost一样是对GBDT的高效实现，原理上它和GBDT及XGBoost类似，都采用损失函数的负梯度作为当前决策树的残差近似值，去拟合新的决策树。

LightGBM树的生长方式是垂直方向的，其他的算法都是水平方向的，也就是说Light GBM生长的是树的叶子，其他的算法生长的是树的层次。
LightGBM选择具有最大误差的树叶进行生长，当生长同样的树叶，生长叶子的算法可以比基于层的算法减少更多的loss。

不建议在小数据集上使用LightGBM。LightGBM对过拟合很敏感，对于小数据集非常容易过拟合。对于多小属于小数据集，并没有什么阈值，但是从我的经验，我建议对于10000+以上的数据的时候，再使用LightGBM。

LightGBM在很多方面会比XGBoost表现的更为优秀。它有以下优势：
更快的训练效率
低内存使用
更高的准确率
支持并行化学习
可处理大规模数据
支持直接使用category特征
从下图实验数据可以看出， LightGBM比XGBoost快将近10倍，内存占用率大约为XGBoost的1/6，并且准确率也有提升。
至于LGB为什么比XGB的精度高这一点，我的理解是选择梯度大(残差大)样本来进行特征分裂生成的树，借鉴了Adaboost的更改样本权重的思想。每棵树针对某些特定训练样本有着较好的划分能力，导致每棵树之间的异质性较大，对于效果近似但异质性大的模型加权往往会带来更大的提升。（AdaBoost方法是一种迭代算法，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率。每一个训练样本都被赋予一个权重，表明它被某个分类器选入训练集的概率。如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它被选中的概率就被降低；相反，如果某个样本点没有被准确地分类，那么它的权重就得到提高。通过这样的方式，AdaBoost方法能“聚焦于”那些较难分（更富信息）的样本上。在具体实现上，最初令每个样本的权重都相等，对于第k次迭代操作，我们就根据这些权重来选取样本点，进而训练分类器C_k。然后就根据这个分类器，来提高被它分错的的样本的权重，并降低被正确分类的样本权重。然后，权重更新过的样本集被用于训练下一个分类器C_k^[2]。整个训练过程如此迭代地进行下去。）

 

 

通俗解释：LGB的优化方法是，在保留大梯度样本的同时，随机地保留一些小梯度样本，同时放大了小梯度样本带来的信息增益。

这样说起来比较抽象，我们过一遍流程： 首先把样本按照梯度排序，选出梯度最大的a%个样本，然后在剩下小梯度数据中随机选取b%个样本，在计算信息增益的时候，将选出来b%个小梯度样本的信息增益扩大 1 - a / b 倍。这样就会避免对于数据分布的改变。

这给我的感觉就是一个公寓里本来住了十个人，感觉太挤了，赶走了六个人，但剩下的四个人要分摊他们六个人的房租。
举个例子，对于一列特征[1,nan,1,nan,1]和一列特征[nan,1,nan,1,nan]，他们正好可以合并成一列特征[1,2,1,2,1]。LGB的目标就是在于找到这样的特征并且将他们合并在一起。

如果把特征抽象成图中的点，特征之间的冲突看作是图中的边，那么问题就转换为找出图中的社团并使图中的社团数量最少。LGB里提出了一个贪心的策略，按照有权度来为图中所有的点排序，然后把特征合并到度小于某个阈值的社团中或单独创建一个社团。

对于特征如何合并，一个重要的原则就是使合并的两个特征可以被顺利区分出来，LGB采取了一个更改阈值的方法。例如对于特征x∈(0, 10)， 特征y∈(0, 20)，就可以把特征y转换为y∈(10,30)，然后再去合并x与y。
看完这些惊人的实验结果以后，对下面两个问题产生了疑惑：XGBoost已经十分完美了，为什么还要追求速度更快、内存使用更小的模型？对GBDT算法进行改进和提升的技术细节是什么？

提出LightGBM的动机

常用的机器学习算法，例如神经网络等算法，都可以以mini-batch的方式训练，训练数据的大小不会受到内存限制。而GBDT在每一次迭代的时候，都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小；如果不装进内存，反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据，普通的GBDT算法是不能满足其需求的。

LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题，让GBDT可以更好更快地用于工业实践。

XGBoost的优缺点

精确贪心算法

每轮迭代时，都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小；如果不装进内存，反复地读写训练数据又会消耗非常大的时间。

优点：

可以找到精确的划分条件
缺点：

计算量巨大
内存占用巨大
易产生过拟合
Level-wise迭代方式

预排序方法（pre-sorted）：首先，空间消耗大。这样的算法需要保存数据的特征值，还保存了特征排序的结果（例如排序后的索引，为了后续快速的计算分割点，在这里XGBoost采用了特征粒度的并行化），这里需要消耗训练数据两倍的内存。其次时间上也有较大的开销，在遍历每一个分割点的时候，都需要进行分裂增益的计算，消耗的代价大。

优点：

可以使用多线程
可以加速精确贪心算法
缺点：

效率低下，可能产生不必要的叶结点
对cache优化不友好
在预排序后，特征对梯度的访问是一种随机访问，并且不同的特征访问的顺序不一样，无法对cache进行优化。同时，在每一层长树的时候，需要随机访问一个行索引到叶子索引的数组，并且不同特征访问的顺序也不一样，也会造成较大的cache miss。

LightGBM在哪些地方进行了优化？

概括来说，lightGBM主要有以下特点：
基于Histogram的决策树算法
带深度限制的Leaf-wise的叶子生长策略
直方图做差加速
直接支持类别特征(Categorical Feature)
Cache命中率优化
基于直方图的稀疏特征优化
多线程优化

XGBoost使用的是pre-sorted算法，能够更精确的找到数据分隔点。

首先，对所有特征按数值进行预排序。
其次，在每次的样本分割时，用O(# data)的代价找到每个特征的最优分割点。
最后，找到最后的特征以及分割点，将数据分裂成左右两个子节点。
这种pre-sorting算法能够准确找到分裂点，但是在空间和时间上有很大的开销。

由于需要对特征进行预排序并且需要保存排序后的索引值（为了后续快速的计算分裂点），因此内存需要训练数据的两倍。
在遍历每一个分割点的时候，都需要进行分裂增益的计算，消耗的代价大。
LightGBM使用的是histogram算法，占用的内存更低，数据分隔的复杂度更低。其思想是将连续的浮点特征离散成k个离散值，并构造宽度为k的Histogram。然后遍历训练数据，统计每个离散值在直方图中的累计统计量。在进行特征选择时，只需要根据直方图的离散值，遍历寻找最优的分割点。

使用直方图算法有很多优点。首先最明显就是内存消耗的降低，直方图算法不仅不需要额外存储预排序的结果，而且可以只保存特征离散化后的值，而这个值一般用8位整型存储就足够了，内存消耗可以降低为原来的1/8。

Histogram algorithm

Histogram algorithm应该翻译为直方图算法，直方图算法的思想也很简单，首先将连续的浮点数据转换为bin数据，具体过程是首先确定对于每一个特征需要多少的桶bin，然后均分，将属于该桶的样本数据更新为bin的值，最后用直方图表示。（看起来很高大上，其实就是直方图统计，最后我们将大规模的数据放在了直方图中）

直方图算法有几个需要注意的地方：

使用bin替代原始数据相当于增加了正则化；
使用bin意味着很多数据的细节特征被放弃了，相似的数据可能被划分到相同的桶中，这样的数据之间的差异就消失了；
bin数量选择决定了正则化的程度，bin越少惩罚越严重，欠拟合风险越高。
直方图算法需要注意的地方：

构建直方图时不需要对数据进行排序（比XGBoost快），因为预先设定了bin的范围；
直方图除了保存划分阈值和当前bin内样本数以外还保存了当前bin内所有样本的一阶梯度和（一阶梯度和的平方的均值等价于均方损失）；
阈值的选取是按照直方图从小到大遍历，使用了上面的一阶梯度和，目的是得到划分之后△loss最大的特征及阈值。

Histogram 算法的优缺点：

Histogram算法并不是完美的。由于特征被离散化后，找到的并不是很精确的分割点，所以会对结果产生影响。但在实际的数据集上表明，离散化的分裂点对最终的精度影响并不大，甚至会好一些。原因在于decision tree本身就是一个弱学习器，采用Histogram算法会起到正则化的效果，有效地防止模型的过拟合。
时间上的开销由原来的O(#data * #features)降到O(k * #features)。由于离散化，#bin远小于#data，因此时间上有很大的提升。
Histogram算法还可以进一步加速。一个叶子节点的Histogram可以直接由父节点的Histogram和兄弟节点的Histogram做差得到。一般情况下，构造Histogram需要遍历该叶子上的所有数据，通过该方法，只需要遍历Histogram的k个捅。速度提升了一倍。

决策树生长策略

在Histogram算法之上，LightGBM进行进一步的优化。首先它抛弃了大多数GBDT工具使用的按层生长 (level-wise)的决策树生长策略，而使用了带有深度限制的按叶子生长 (leaf-wise)算法。

XGBoost采用的是按层生长level（depth）-wise生长策略，能够同时分裂同一层的叶子，从而进行多线程优化，不容易过拟合；但不加区分的对待同一层的叶子，带来了很多没必要的开销。因为实际上很多叶子的分裂增益较低，没必要进行搜索和分裂。

LightGBM采用leaf-wise生长策略，每次从当前所有叶子中找到分裂增益最大（一般也是数据量最大）的一个叶子，然后分裂，如此循环。因此同Level-wise相比，在分裂次数相同的情况下，Leaf-wise可以降低更多的误差，得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树，产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制，在保证高效率的同时防止过拟合。

直方图差加速

LightGBM另一个优化是Histogram（直方图）做差加速。一个容易观察到的现象：一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。通常构造直方图，需要遍历该叶子上的所有数据，但直方图做差仅需遍历直方图的k个桶。利用这个方法，LightGBM可以在构造一个叶子的直方图后，可以用非常微小的代价得到它兄弟叶子的直方图，在速度上可以提升一倍。

直接支持类别特征

实际上大多数机器学习工具都无法直接支持类别特征，一般需要把类别特征，转化one-hotting特征，降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑，LightGBM优化了对类别特征的支持，可以直接输入类别特征，不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则。

one-hot编码是处理类别特征的一个通用方法，然而在树模型中，这可能并不一定是一个好的方法，尤其当类别特征中类别个数很多的情况下。主要的问题是：

可能无法在这个类别特征上进行切分（即浪费了这个特征）。使用one-hot编码的话，意味着在每一个决策节点上只能使用one vs rest（例如是不是狗，是不是猫等）的切分方式。当类别值很多时，每个类别上的数据可能会比较少，这时候切分会产生不平衡，这意味着切分增益也会很小（比较直观的理解是，不平衡的切分和不切分没有区别）。
会影响决策树的学习。因为就算可以在这个类别特征进行切分，也会把数据切分到很多零碎的小空间上，如图1左边所示。而决策树学习时利用的是统计信息，在这些数据量小的空间上，统计信息不准确，学习会变差。但如果使用下图右边的分裂方式，数据会被切分到两个比较大的空间，进一步的学习也会更好。
下图右边叶子节点的含义是X=A或者X=C放到左孩子，其余放到右孩子。

LightGBM处理分类特征大致流程

为了解决one-hot编码处理类别特征的不足。LightGBM采用了Many vs many的切分方式，实现了类别特征的最优切分。用LightGBM可以直接输入类别特征，并产生上图右边的效果。在1个k维的类别特征中寻找最优切分，朴素的枚举算法的复杂度是O(2k)，而LightGBM采用了如On Grouping For Maximum Homogeneity的方法实现了O(klogk)的算法。

算法流程下图所示：在枚举分割点之前，先把直方图按每个类别的均值进行排序；然后按照均值的结果依次枚举最优分割点。从下图可以看到，Sum(y)/Count(y)为类别的均值。当然，这个方法很容易过拟合，所以在LGBM中加入了很多对这个方法的约束和正则化。
下图是一个简单的对比实验，可以看到该最优方法在AUC上提升了1.5个点，并且时间只多了20%。
下面具体来讲下在代码中如何求解类别特征的最优切分的流程：

离散特征建立直方图的过程：统计该特征下每一种离散值出现的次数，并从高到低排序，并过滤掉出现次数较少的特征值, 然后为每一个特征值，建立一个bin容器, 对于在bin容器内出现次数较少的特征值直接过滤掉，不建立bin容器。
计算分裂阈值的过程：
先看该特征下划分出的bin容器的个数，如果bin容器的数量小于4，直接使用one vs other方式, 逐个扫描每一个bin容器，找出最佳分裂点;
对于bin容器较多的情况, 先进行过滤，只让子集合较大的bin容器参加划分阈值计算, 对每一个符合条件的bin容器进行公式计算:

公式如下: 该bin容器下所有样本的一阶梯度之和/该bin容器下所有样本的二阶梯度之和 + 正则项(参数cat_smooth)

这里为什么不是label的均值呢？其实上例中只是为了便于理解，只针对了学习一棵树且是回归问题的情况， 这时候一阶导数是Y, 二阶导数是1)，得到一个值，根据该值对bin容器从小到大进行排序，然后分从左到右、从右到左进行搜索，得到最优分裂阈值。但是有一点，没有搜索所有的bin容器，而是设定了一个搜索bin容器数量的上限值，程序中设定是32，即参数max_num_cat。LightGBM中对离散特征实行的是many vs many 策略，这32个bin中最优划分的阈值的左边或者右边所有的bin容器就是一个many集合，而其他的bin容器就是另一个many集合。
对于连续特征，划分阈值只有一个，对于离散值可能会有多个划分阈值，每一个划分阈值对应着一个bin容器编号，当使用离散特征进行分裂时，只要数据样本对应的bin容器编号在这些阈值对应的bin集合之中，这条数据就加入分裂后的左子树，否则加入分裂后的右子树。

直接支持高效并行

LightGBM原生支持并行学习，目前支持特征并行和数据并行的两种。特征并行的主要思想是在不同机器在不同的特征集合上分别寻找最优的分割点，然后在机器间同步最优的分割点。数据并行则是让不同的机器先在本地构造直方图，然后进行全局的合并，最后在合并的直方图上面寻找最优分割点。
LightGBM针对这两种并行方法都做了优化，在特征并行算法中，通过在本地保存全部数据避免对数据切分结果的通信；在数据并行中使用分散规约(Reduce scatter)把直方图合并的任务分摊到不同的机器，降低通信和计算，并利用直方图做差，进一步减少了一半的通信量。
基于投票的数据并行则进一步优化数据并行中的通信代价，使通信代价变成常数级别。在数据量很大的时候，使用投票并行可以得到非常好的加速效果。

网络通信优化

XGBoost由于采用pre-sorted算法，通信代价非常大，所以在并行的时候也是采用histogram算法；LightGBM采用的histogram算法通信代价小，通过使用集合通信算法，能够实现并行计算的线性加速。

LightGBM原理

提升树是利用加模型与前向分布算法实现学习的优化过程，它有一些高效实现，如XGBoost, pGBRT，GBDT(Gradient Boosting Decision Tree)等。其中GBDT采用负梯度作为划分的指标（信息增益），XGBoost则利用到二阶导数。他们共同的不足是，计算信息增益需要扫描所有样本，从而找到最优划分点。在面对大量数据或者特征维度很高时，它们的效率和扩展性很难使人满意。解决这个问题的直接方法就是减少特征量和数据量而且不影响精确度，有部分工作根据数据权重采样来加速booisting的过程，但由于GBDT没有样本权重不能应用。

结合使用 GOSS 和 EFB 的 GBDT 算法就是 LightGBM。微软开源的LightGBM（基于GBDT的）则很好的解决这些问题，它主要包含两个算法：

单边梯度采样，Gradient-based One-Side Sampling（GOSS）

GOSS（从减少样本角度）：排除大部分小梯度的样本，仅用剩下的样本计算信息增益。GBDT虽然没有数据权重，但每个数据实例有不同的梯度，根据计算信息增益的定义，梯度大的实例对信息增益有更大的影响，因此在下采样时，我们应该尽量保留梯度大的样本（预先设定阈值，或者最高百分位间），随机去掉梯度小的样本。我们证明此措施在相同的采样率下比随机采样获得更准确的结果，尤其是在信息增益范围较大时。

GBDT使用决策树，来学习获得一个将输入空间映射到梯度空间的函数。假设训练集有n个实例x1,…,xn，特征维度为s。每次梯度迭时，模型数据变量的损失函数的负梯度方向表示为g1,…,gn，决策树通过最优切分点（最大信息增益点）将数据分到各个节点。GBDT通过分割后的方差衡量信息增益。

GOSS是一种在减少数据量和保证精度上平衡的算法。GOSS是通过区分不同梯度的实例，保留较大梯度实例同时对较小梯度随机采样的方式减少计算量，从而达到提升效率的目的。

EFB是通过特征捆绑的方式减少特征维度（其实是降维技术）的方式，来提升计算效率。通常被捆绑的特征都是互斥的（一个特征值为零,一个特征值不为零），这样两个特征捆绑起来才不会丢失信息。如果两个特征并不是完全互斥（部分情况下两个特征都是非零值），可以用一个指标对特征不互斥程度进行衡量，称之为冲突比率，当这个值较小时，我们可以选择把不完全互斥的两个特征捆绑，而不影响最后的精度。

AdaBoost中，样本权重是数据实例重要性的指标。然而在GBDT中没有原始样本权重，不能应用权重采样。幸运的事，我们观察到GBDT中每个数据都有不同的梯度值，对采样十分有用，即实例的梯度小，实例训练误差也就较小，已经被学习得很好了，直接想法就是丢掉这部分梯度小的数据。然而这样做会改变数据的分布，将会影响训练的模型的精确度，为了避免此问题，我们提出了GOSS。

GOSS保留所有的梯度较大的实例，在梯度小的实例上使用随机采样。为了抵消对数据分布的影响，计算信息增益的时候，GOSS对小梯度的数据引入常量乘数。GOSS首先根据数据的梯度绝对值排序，选取top a个实例。然后在剩余的数据中随机采样b个实例。接着计算信息增益时为采样出的小梯度数据乘以(1-a)/b，这样算法就会更关注训练不足的实例，而不会过多改变原数据集的分布。

定义：O表示某个固定节点的训练集，分割特征j的分割点d定义为：

其中，

在GOSS中，
首先根据数据的梯度将训练降序排序。
保留top a个数据实例，作为数据子集A。
对于剩下的数据的实例，随机采样获得大小为b的数据子集B。
最后我们通过以下方程估计信息增益: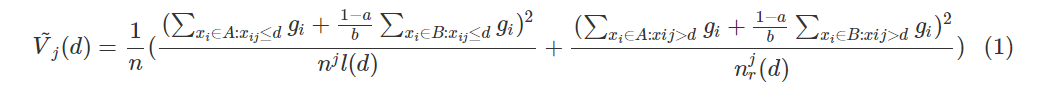

此处GOSS通过较小的数据集估计信息增益V~j(d)将大大地减小计算量。更重要的，我们接下来理论表明GOSS不会丢失许多训练精度，胜过随机采样，理论的证明在附加材料。

我们定义GOSS近似误差为：
根据上述理论，我们得出以下结论：

GOSS流程

输入：训练数据，迭代步数d，大梯度数据的采样率a，小梯度数据的采样率b，损失函数和若学习器的类型（一般为决策树）；

输出：训练好的强学习器；

（1）根据样本点的梯度的绝对值对它们进行降序排序；

（2）对排序后的结果选取前a*100%的样本生成一个大梯度样本点的子集；

（3）对剩下的样本集合（1-a）100%的样本，随机的选取b（1-a）*100%个样本点，生成一个小梯度样本点的集合；

（4）将大梯度样本和采样的小梯度样本合并；

（5）将小梯度样本乘上一个权重系数；

（6）使用上述的采样的样本，学习一个新的弱学习器；

（7）不断地重复（1）~（6）步骤直到达到规定的迭代次数或者收敛为止。

通过上面的算法可以在不改变数据分布的前提下不损失学习器精度的同时大大的减少模型学习的速率。

从上面的描述可知，当a=0时，GOSS算法退化为随机采样算法；当a=1时，GOSS算法变为采取整个样本的算法。在许多情况下，GOSS算法训练出的模型精确度要高于随机采样算法。另一方面，采样也将会增加若学习器的多样性，从而潜在的提升了训练出的模型泛化能力。

互斥特征绑定，Exclusive Feature Bundling（EFB）

EFB（从减少特征角度）：捆绑互斥特征，也就是他们很少同时取非零值（也就是用一个合成特征代替）。通常真是应用中，虽然特征量比较多，但是由于特征空间十分稀疏，是否可以设计一种无损的方法来减少有效特征呢？特别在稀疏特征空间上，许多特征几乎是互斥的（例如许多特征不会同时为非零值，像one-hot），我们可以捆绑互斥的特征。最后，我们将捆绑问题归约到图着色问题，通过贪心算法求得近似解。
结合使用 GOSS 和 EFB 的 GBDT 算法就是 LightGBM。

EBF的算法步骤如下：

将特征按照非零值的个数进行排序
计算不同特征之间的冲突比率
遍历每个特征并尝试合并特征，使冲突比率最小化
高位的数据通常是稀疏的，这种稀疏性启发我们设计一种无损地方法来减少特征的维度。特别的，稀疏特征空间中，许多特征是互斥的，例如他们从不同时为非零值。我们可以绑定互斥的特征为单一特征，通过仔细设计特征臊面算法，我们从特征捆绑中构建了与单个特征相同的特征直方图。这种方式的间直方图时间复杂度从O(#data * #feature)降到O(#data * #bundle)，由于#bundle << # feature，我们能够极大地加速GBDT的训练过程而且损失精度。

有两个问题：

怎么判定那些特征应该绑在一起（build bundled）？
怎么把特征绑为一个（merge feature）？
bundle（什么样的特征被绑定）？

**理论1：**将特征分割为较小量的互斥特征群是NP难的。

证明：将图着色问题归约为此问题，而图着色是NP难的，所以此问题就是NP难的。

给定图着色实例G=(V, E)。以G的关联矩阵的每一行为特征，得到我们问题的一个实例有|V|个特征。 很容易看到，在我们的问题中，一个独特的特征包与一组具有相同颜色的顶点相对应，反之亦然。

理论1说明多项式时间中求解这个NP难问题不可行。为了寻找好的近似算法，我们将最优捆绑问题归结为图着色问题，如果两个特征之间不是相互排斥，那么我们用一个边将他们连接，然后用合理的贪婪算法（具有恒定的近似比）用于图着色来做特征捆绑。 此外，我们注意到通常有很多特征，尽管不是100％相互排斥的，也很少同时取非零值。 如果我们的算法可以允许一小部分的冲突，我们可以得到更少的特征包，进一步提高计算效率。经过简单的计算，随机污染小部分特征值将影响精度最多O([(1–γ)n]−2/3)，γ是每个绑定中的最大冲突比率，当其相对较小时，能够完成精度和效率之间的平衡。

基于上面的讨论，我们设计了算法3，伪代码见下图，具体算法：

建立一个图，每个点代表特征，每个边有权重，其权重和特征之间总体冲突相关。
按照降序排列图中的度数来排序特征。
检查排序之后的每个特征，对他进行特征绑定或者建立新的绑定使得操作之后的总体冲突最小。
算法3的时间复杂度是O(feature2)，训练之前只处理一次，其时间复杂度在特征不是特别多的情况下是可以接受的，但难以应对百万维的特征。为了继续提高效率，我们提出了一个更加高效的无图的排序策略：将特征按照非零值个数排序，这和使用图节点的度排序相似，因为更多的非零值通常会导致冲突，新算法在算法3基础上改变了排序策略。

merging features(特征合并)

如何合并同一个bundle的特征来降低训练时间复杂度。关键在于原始特征值可以从bundle中区分出来。鉴于直方图算法存储离散值而不是连续特征值，我们通过将互斥特征放在不同的箱中来构建bundle。这可以通过将偏移量添加到特征原始值中实现，例如，假设bundle中有两个特征，原始特征A取值[0, 10]，B取值[0, 20]。我们添加偏移量10到B中，因此B取值[10, 30]。通过这种做法，就可以安全地将A、B特征合并，使用一个取值[0, 30]的特征取代AB。算法见算法4，

EFB算法能够将许多互斥的特征变为低维稠密的特征，就能够有效的避免不必要0值特征的计算。实际，通过用表记录数据中的非零值，来忽略零值特征，达到优化基础的直方图算法。通过扫描表中的数据，建直方图的时间复杂度将从O(#data)降到O(#non_zero_data)。当然，这种方法在构建树过程中需要而额外的内存和计算开销来维持预特征表。我们在lightGBM中将此优化作为基本函数，因为当bundles是稀疏的时候，这个优化与EFB不冲突（可以用于EFB）。
参考链接：https://blog.csdn.net/shine19930820/article/details/79123216

针对 Leaf-wise（Best-first）树的参数优化

（1）num_leaves这是控制树模型复杂度的主要参数。理论上, 借鉴 depth-wise 树, 我们可以设置 num_leaves= 但是, 这种简单的转化在实际应用中表现不佳. 这是因为, 当叶子数目相同时, leaf-wise 树要比 depth-wise 树深得多, 这就有可能导致过拟合. 因此, 当我们试着调整 num_leaves 的取值时, 应该让其小于 . 举个例子, 当 max_depth=7时，depth-wise 树可以达到较高的准确率.但是如果设置 num_leaves 为 128 时, 有可能会导致过拟合, 而将其设置为 70 或 80 时可能会得到比 depth-wise 树更高的准确率. 其实, depth 的概念在 leaf-wise 树中并没有多大作用, 因为并不存在一个从 leaves 到 depth 的合理映射。

（2）min_data_in_leaf. 这是处理 leaf-wise 树的过拟合问题中一个非常重要的参数. 它的值取决于训练数据的样本个树和 num_leaves. 将其设置的较大可以避免生成一个过深的树, 但有可能导致欠拟合. 实际应用中, 对于大数据集, 设置其为几百或几千就足够了。

（3）max_depth（默认不限制，一般设置该值为5—10即可） 你也可以利用 max_depth 来显式地限制树的深度。

5.2 针对更快的训练速度

（1）通过设置 bagging_fraction 和 bagging_freq 参数来使用 bagging 方法；

（2）通过设置 feature_fraction 参数来使用特征的子抽样；

（3）使用较小的 max_bin；

（4）使用 save_binary 在以后的学习过程对数据进行加速加载。

• 1
• 2
• 3
• 4
• 5
• 6
• 7

5.3 针对更好的准确率

（1）使用较大的 max_bin （学习速度可能变慢）；

（2）使用较小的 learning_rate 和较大的 num_iterations；

（3）使用较大的 num_leaves （可能导致过拟合）；

（4）使用更大的训练数据；

（5）尝试 dart（一种在多元Additive回归树种使用dropouts的算法）.

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

5.4 处理过拟合

（1）使用较小的 max_bin（默认为255）

（2）使用较小的 num_leaves（默认为31）

（3）使用 min_data_in_leaf（默认为20） 和 min_sum_hessian_in_leaf（默认为）

（4）通过设置 bagging_fraction （默认为1.0）和 bagging_freq （默认为0，意味着禁用bagging，k表示每k次迭代执行一个bagging）来使用 bagging

（5）通过设置 feature_fraction（默认为1.0） 来使用特征子抽样

（6）使用更大的训练数据

（7）使用 lambda_l1（默认为0）, lambda_l2 （默认为0）和 min_split_gain（默认为0，表示执行切分的最小增益） 来使用正则

（8）尝试 max_depth 来避免生成过深的树

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16

具体想要了解更多内容请参考：
https://blog.csdn.net/qq_24519677/article/details/82811215

附上python3代码

#数据预处理
import numpy as np	
import matplotlib.pyplot as plt	
import pandas as pd	
# Importing the dataset	
dataset = pd.read_csv('...input\\Social_Network_Ads.csv')	
X = dataset.iloc[:, [2, 3]].values	
y = dataset.iloc[:, 4].values	
# Splitting the dataset into the Training set and Test set	
from sklearn.cross_validation import train_test_split	
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)	
# Feature Scaling	
from sklearn.preprocessing import StandardScaler	
sc = StandardScaler()	
x_train = sc.fit_transform(x_train)	
x_test = sc.transform(x_test)
#模型构建和训练
import lightgbm as lgb	
d_train = lgb.Dataset(x_train, label=y_train)	
params = {}	
params['learning_rate'] = 0.003	
params['boosting_type'] = 'gbdt'	
params['objective'] = 'binary'	
params['metric'] = 'binary_logloss'	
params['sub_feature'] = 0.5	
params['num_leaves'] = 10	
params['min_data'] = 50	
params['max_depth'] = 10	
clf = lgb.train(params, d_train, 100)
#模型预测
#Prediction	
y_pred=clf.predict(x_test)	
#convert into binary values	
for i in range(0,99):	
    if y_pred[i]>=.5:       # setting threshold to .5	
       y_pred[i]=1	
    else:  	
       y_pred[i]=0
#准确率计算
#Confusion matrix	
from sklearn.metrics import confusion_matrix	
cm = confusion_matrix(y_test, y_pred)	
#Accuracy	
from sklearn.metrics import accuracy_score	
accuracy=accuracy_score(y_pred,y_test)

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46

结果：

调参:

数据科学家在使用参数的时候，总是很挣扎。理想的参数应该长什么样呢？下面的一组练习可以用来提升你的模型效率。

num_leaves: 这个是控制树的复杂度的主要的参数。理想情况下，叶子的数量的值应该小于等于 $2^{max_depth}$，大于这个值会导致过拟合。
mindatain_leaf: 设置成一个比较大的值可以避免树生长太深，但是可能会导致过拟合。实际使用中，对于大数据集设置成几百到几千就足够了。

maxdepth: 你可以使用maxdepth来显式的限制深度。

• 1
• 2
• 3
• 4

追求速度:

通过设置 bagging_fraction 和 bagging_freq来使用bagging

通过设置 feature_fraction来使用特征下采样

使用小的 max_bin

使用 save_binary 来加速加载数据

使用并行学习，参考parallel learning guide

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

追求更高的准确率:

使用大的 max_bin (可能速度会慢)

使用小 learning_rate 大的 num_iterations

使用大的 num_leaves(可能会过拟合)

使用大训练数据集

试试 dart

尝试直接使用类别特征

处理过拟合:

使用小的 max_bin

使用小的 num_leaves

使用 min_data_in_leaf 和 min_sum_hessian_in_leaf

通过设置 bagging_fraction 和 bagging_freq来使用bagging

通过设置 feature_fraction来使用特征下采样`

使用大训练数据集

尝试使用 lambda_l1, lambda_l2 和 min_gain_to_split 来进行正则化

尝试使用 max_depth 来避免生成的树太深