半监督学习分类——？？？

半监督学习

主动学习

用已标记样本训练出一个模型，用模型对未标记样本进行预测，选出对改善性能有帮助（比如选出那些不太确定的未标记样本）的样本，向专家征求最终标记的意见，并将专家意见作为标记，将该样本加入训练集得出新模型，不断重复这个工作。

关键：外界因素，即专家经验；

半监督学习

让学习器不依赖外界交互、自动地利用未标记样本提升学习性能，就是半监督学习；当然也可以用这种方法给金融样本打标签，进行拒绝推断。

纯半监督学习，其实就是充分利用已标记样本与未标记样本，得到一个模型，具有相当好的预测性；而直推学习，其实就是利用已知与未知标记样本建模，最终得到未标记样本的标签的预测。前者是得到了高泛化能力的模型，后者是得到未知标记样本的最优预测；其实可以看做是一回事。

通常需要做出一些假设，即未标记样本的数据分布信息与已标记样本直接相联系。

生成式方法(generative methods)

假设所有的数据，不论标记与否都由同一个潜在的模型生成的；而未标记数据的标记看作是潜在模型的缺失参数。使用EM算法（专门求解含有隐变量的参数解问题）进行求解，相当于潜在模型的缺失参数是隐变量，模型的假设不同，方法不同。

这种方法在有标记数据极少的情形下往往比其他方法性能更好。

关键：模型假设必须准确，否则会降低泛化性能；这需要充分可靠的领域知识。

模型假设：比如高斯混合模型、混合专家模型、朴素贝叶斯模型。

学习到：最终得到样本的概率（当然也看假设的模型是什么）。

半监督SVM

半监督支持向量机（semi-supervised support vector machine，简称为S3VM）。

在不考虑标记样本时，SVM试图找到最大间隔划分的超平面，而考虑未标记样本后，S3VM试图找到的，是能够将两类有标记样本分开，同时要穿过数据低密度区域的超平面。（之所以要穿过低密度区，是因为存在未标记样本，有一些聚类的思想）

 

 

TSVM算法，针对二分类问题：

步骤：

首先利用有标记样本学得一个SVM，利用该分类器对未标记数据进行标记指派，并将结果当做真实标记重新训练一个SVM，可以得出新的超平面和松弛向量，因为此时的未标记样本不准确，所有Cu<Cl，使得已标记样本所占比重更大；

之后找出两个标记指派为异类的且很可能发生错误的未标记样本，交换它们的标记，继续训练SVM得到超平面和松弛向量；

再继续重复上个过程直到标记调整完成；逐渐增大Cu的值，直到Cu=Cl。

此时可以得到未标记样本的标记，

Dl为已知标记的样本，Du是未知标记的样本。

 

 

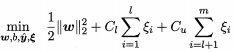
存在的问题：计算开销很大；若存在多个低密度划分，则效果很差。

针对高效优化求解问题，有基于图核（graph kernel）函数梯度下降的LDS、基于标记均值估计的meanS3VM等。

或许可以这样理解，其实就是使用SVM算法进行预测，只是加入的调整SVM模型的步骤（反复试错），不断迭代调整，找到使得所有样本（包括已标记和未标记）的良好的分割面。

图半监督学习

即标签传播算法，基于高斯核来定义两样本的相似度/边的权重（每个样本就是一个节点，相连的边的强度就是权重大小）。

 

 

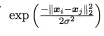
每个节点的标签按相似度传播给相邻节点，在节点传播的每一步，每个节点都根据相邻节点的标签来更新自己的标签，与该节点相似度越大，则相邻节点对其标注的影响权值越大，节点的标签更趋于一致。传播过程中，已标记数据的标签不变，最终迭代结束时，相似节点的概率分布也趋于相似。

 

关键：图的质量很重要，常用高斯距离图、k近邻图、ε近邻图。

存在的问题：1.存储开销大，难以处理大规模数据；2.接收到新样本时，需要对图进行重构并重新进行标记传播；当然，可以引入预测机制，将更新的未标记样本作为训练集的一部分，单独训练一个模型对新样本进行预测。

 

或许可以这样理解：就是近邻与基于距离的聚类思想，相似的样本具有相似的标记。

基于分歧的方法

协同训练（co-training），协同训练能够很好的利用不同特征之间，不同模型之间，不同数据采样，甚至不同参数产生的不同学习器，利用它们之间的相容性与互补性，提高弱分类器的泛化能力。

原本是针对多视图数据设计的，多视图就是样本对象有多个属性集，每个属性集就是一个视图。比如电影中的画面类和声音类就是两个视图。

相容性：即视图最终的输出空间（输出结果范围）是一致的：{好，坏}，{+1，-1}。

互补性：各自提供了不同的视角看待问题，相互补充，集成的思想。

关键：使得分类器之间存在显著的差异。

可以通过不同的特征、不同的算法、不同的数据采样、不同参数设置来得到这些差异。

 

具体过程：

前提：数据拥有两个充分且条件独立的视图。充分是每个视图都包含足以产生最优学习器的信息，条件独立是指非定类别标记条件下两个视图独立。（即将数据分成两部分，每个部分都能得到较好的分类器）

首先，使用每个视图基于有标记样本分别训练出一个分类器；

之后，利用这两个分类器，均对所有未标记样本进行预测，并挑选出各自分类器中置信度最高的那些交给另一个分类器重新训练模型；

重复这样的操作，直到终止。

 

选择合适的基学习器很重要！不同特征、不同算法、不同数据采用、不同参数设置等仅是产生差异的方法。

 

或许可以这样理解：就是利用两个分类器（有显著不同的两个）进行预测，并结合了迭代调整的过程（分别取出单个分类器预测较准确的值交给另一个作为已标记样本，训练模型），还拥有一个特点是集成的思想（不同分类器从不同的角度学习样本，综合起来效果更好），最终得到两个分类器相互调整建模预测的结果。

 

半监督聚类

先将已知类别聚类得到各类别的聚类中心，再根据已知类别样本聚类结果，扩展到未标记样本继续聚类，已知类别的标记始终不变。

本质：k均值聚类的距离相似性来判断标签。

 

流形假设

假设数据分布在一个流形结构上，邻近的样本拥有相似的输出值。邻近程度用相似程度来刻画，可以说是聚类的假设的推广。本质与聚类假设是相同的：相似的样本具有相似的输出！

上述这些方法的思想或许可以分为两种：

近邻与聚类的思想，直接或间接的衡量样本的空间分布信息，根据空间分布情况来进行预测；分类器集成预测的思想，利用的是不同分类器从不同角度学习数据，并进行预测。