栈队列 hash表堆算法模板和相关题目

什么是栈（Stack）？

栈（stack）是一种采用后进先出（LIFO，last in first out）策略的抽象数据结构。比如物流装车，后装的货物先卸，先转的货物后卸。栈在数据结构中的地位很重要，在算法中的应用也很多，比如用于非递归的遍历二叉树，计算逆波兰表达式，等等。

栈一般用一个存储结构（常用数组，偶见链表），存储元素。并用一个指针记录栈顶位置。栈底位置则是指栈中元素数量为0时的栈顶位置，也即栈开始的位置。
栈的主要操作：

push()，将新的元素压入栈顶，同时栈顶上升。
pop()，将新的元素弹出栈顶，同时栈顶下降。
empty()，栈是否为空。
peek()，返回栈顶元素。

在各语言的标准库中：

Java，使用java.util.Stack，它是扩展自Vector类，支持push()，pop()，peek()，empty()，search()等操作。
C++，使用<stack>中的stack即可，方法类似Java，只不过C++中peek()叫做top()，而且pop()时，返回值为空。
Python，直接使用list，查看栈顶用[-1]这样的切片操作，弹出栈顶时用list.pop()，压栈时用list.append()。

如何自己实现一个栈？

参见问题：http://www.lintcode.com/en/problem/implement-stack/
这里给出一种用ArrayList的通用实现方法。（注意：为了将重点放在栈结构上，做了适当简化。该栈仅支持整数类型，若想实现泛型，可用反射机制和object对象传参；此外，可多做安全检查并抛出异常）

Python

class Stack:
    def __init__(self):
        self.array = []
				
    # 压入新元素
    def push(self, x):
        self.array.append(x)
    
    # 栈顶元素出栈
    def pop(self):
        if not self.isEmpty():
            self.array.pop()
	
    # 返回栈顶元素
    def top(self):
        return self.array[-1]

    # 判断是否是空栈
    def isEmpty(self):
        return len(self.array) == 0

栈在计算机内存当中的应用

我们在程序运行时，常说的内存中的堆栈，其实就是栈空间。这一段空间存放着程序运行时，产生的各种临时变量、函数调用，一旦这些内容失去其作用域，就会被自动销毁。
函数调用其实是栈的很好的例子，后调用的函数先结束，所以为了调用函数，所需要的内存结构，栈是再合适不过了。在内存当中，栈从高地址不断向低地址扩展，随着程序运行的层层深入，栈顶指针不断指向内存中更低的地址。

我们在前面的二叉树的学习中，已经学习了如何使用 Stack 来进行非递归的二叉树遍历。

这里我们来看看栈在面试中的其他一些考点和考题：

如果自己实现一个栈？
如何用两个队列实现一个栈？
用一个数组如何实现三个栈？

队列

定义

队列为一种先进先出的线性表
只允许在表的一端进行入队，在另一端进行出队操作。在队列中，允许插入的一端叫队尾，允许删除的一端叫队头，即入队只能从队尾入，出队只能从队头出

思路

需要两个节点，一个头部节点，也就是dummy节点，它是在加入的第一个元素的前面，也就是dummy.next=第一个元素，这样做是为了方便我们删除元素，还有一个尾部节点，也就是tail节点，表示的是最后一个元素的节点
初始时，tail节点跟dummy节点重合
当我们要加入一个元素时，也就是从队尾中加入一个元素，只需要新建一个值为val的node节点，然后tail.next=node，再移动tail节点到tail.next
当我们需要删除队头元素时，只需要将dummy.next变为dummy.next.next，这样就删掉了第一个元素，这里需要注意的是，如果删掉的是队列中唯一的一个元素，那么需要将tail重新与dummy节点重合
当我们需要得到队头元素而不删除这个元素时，只需要获得dummy.next.val就可以了

示例代码

Python:

class QueueNode:
    def __init__(self, value):
        self.val = value
        self.next = None


class Queue:
    def __init__(self):
        self.dummy = QueueNode(-1)
        self.tail = self.dummy

    def enqueue(self, val):
        node = QueueNode(val)
        self.tail.next = node
        self.tail = node

    def dequeue(self):
        ele = self.dummy.next.val
        self.dummy.next = self.dummy.next.next

        if not self.dummy.next:
            self.tail = self.dummy
        return ele

    def peek(self):
        return self.dummy.next.val

    def isEmpty(self):
        return self.dummy.next == None

队列通常被用作 BFS 算法的主要数据结构。除此之外面试中其他可能考察队列这个数据结构的地方并不多。我们这里把非 BFS 的队列考题考点做一个汇总：

如何用链表实现队列？
如何用两个栈实现一个队列？
什么是循环数组，如何用循环数组实现队列？

什么是循环数组，如何用循环数组实现队列？

什么是循环数组

Circular array = a data structure that used a array as if it were connected end-to-end

可以图示为：

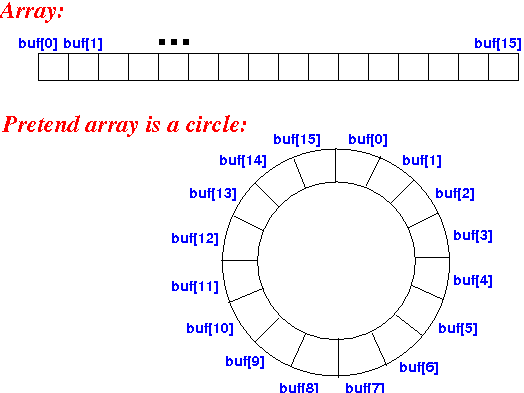
circular array

如何实现队列

我们需要知道队列的入队操作是只在队尾进行的，相对的出队操作是只在队头进行的，所以需要两个变量front与rear分别来指向队头与队尾
由于是循环队列，我们在增加元素时，如果此时 rear = array.length - 1 ，rear 需要更新为 0；同理，在元素出队时，如果 front = array.length - 1, front 需要更新为 0. 对此，我们可以通过对数组容量取模来更新。

示例代码

Python:

class CircularQueue:
    def __init__(self, n):
        self.circularArray = [0]*n
        self.front = 0
        self.rear = 0
        self.size = 0
        
    """
    @return:  return true if the array is full
    """
    def isFull(self):
        return self.size == len(self.circularArray)

    """
    @return: return true if there is no element in the array
    """
    def isEmpty(self):
        return self.size == 0

    """
    @param element: the element given to be added
    @return: nothing
    """
    def enqueue(self, element):
        if self.isFull():
            raise RuntimeError("Queue is already full")
        self.rear = (self.front+self.size) % len(self.circularArray)
        self.circularArray[self.rear] = element
        self.size += 1

    """
    @return: pop an element from the queue
    """
    def dequeue(self):
        if self.isEmpty():
            raise RuntimeError("Queue is already empty")
        ele = self.circularArray[self.front]
        self.front = (self.front+1) % len(self.circularArray)
        self.size -= 1
        return ele

在线练习

http://www.lintcode.com/zh-cn/problem/implement-queue-by-circular-array/#

642. 数据流滑动窗口平均值

样例

样例1 :

MovingAverage m = new MovingAverage(3);
m.next(1) = 1 // 返回 1.00000
m.next(10) = (1 + 10) / 2 // 返回 5.50000
m.next(3) = (1 + 10 + 3) / 3 // 返回 4.66667
m.next(5) = (10 + 3 + 5) / 3 // 返回 6.00000

from collections import deque

class MovingAverage:
    """
    @param: size: An integer
    """
    def __init__(self, size):
        # do intialization if necessary
        self.q = deque()
        self.size = size
        self.sum = 0

    """
    @param: val: An integer
    @return:  
    """
    def next(self, val):
        # write your code here
        if len(self.q) == self.size:
            self.sum -= self.q.popleft()
        self.q.append(val)
        self.sum += val
        return self.sum/len(self.q)
        

# Your MovingAverage object will be instantiated and called as such:
# obj = MovingAverage(size)
# param = obj.next(val)

134. LRU缓存策略

样例

样例 1:

输入：
LRUCache(2)
set(2, 1)
set(1, 1)
get(2)
set(4, 1)
get(1)
get(2)
输出：[1,-1,1]
解释：
cache上限为2，set(2,1)，set(1, 1)，get(2) 然后返回 1，set(4,1) 然后 delete (1,1)，因为 （1,1）最少使用，get(1) 然后返回 -1，get(2) 然后返回 1。

样例 2:

输入：
LRUCache(1)
set(2, 1)
get(2)
set(3, 2)
get(2)
get(3)
输出：[1,-1,2]
解释：
cache上限为 1，set(2,1)，get(2) 然后返回 1，set(3,2) 然后 delete (2,1)，get(2) 然后返回 -1，get(3) 然后返回 2。

from collections import deque

class LRUCache:
    """
    @param: capacity: An integer
    """
    def __init__(self, capacity):
        # do intialization if necessary
        self.cap = capacity
        self.q = deque()
        self.cache = dict()

       
    def move2tail(self, key):  
        self.q.remove(key)
        self.q.append(key)
        
            
    """
    @param: key: An integer
    @return: An integer
    """
    def get(self, key):
        # write your code here
        if key in self.cache:
            self.move2tail(key)
            return self.cache[key]
        else:
            return -1


    """
    @param: key: An integer
    @param: value: An integer
    @return: nothing
    """
    def set(self, key, value):
        # write your code here
        if key in self.cache:
            self.cache[key] = value
            self.move2tail(key)
        else:
            if len(self.q) == self.cap:
                del self.cache[self.q.popleft()]
            self.q.append(key)
            self.cache[key] = value

这个实现的时间复杂度有点高，更新的时候是O（n），使用hash+双向链表是最优的思路，其中hash存储的是链表的节点地址。还是有点繁琐，代码较多，一次性写对比较难，我自己写的：

class Node(object):
    def __init__(self, val=None, pre=None, next=None):
        self.val = val
        self.pre = pre
        self.next = next


class LinkList(object):
    def __init__(self):
        self.dummy = Node()
        self.tail = None
        self.size = 0

    def append(self, value):
        new_node = Node(value)
        if self.tail is None:
            self.tail = new_node
            self.dummy.next = new_node
            new_node.pre = self.dummy
        else:
            self.tail.next = new_node
            new_node.pre = self.tail
            self.tail = new_node
        self.size += 1
        return new_node

    def popleft(self):
        pop_node = self.dummy.next
        self.remove(pop_node)
        return pop_node

    def remove(self, node):
        if not node:
            return
        pre_node = node.pre
        next_node = node.next
        if pre_node:
            pre_node.next = next_node
        if next_node:
            next_node.pre = pre_node
        else:
            self.tail = pre_node
        self.size -= 1

    def __len__(self):
        return self.size


class LRUCache:
    """
    @param: capacity: An integer
    """

    def __init__(self, capacity):
        # do intialization if necessary
        self.cap = capacity
        self.q = LinkList()
        self.cache = dict()

    def move2tail(self, key, value=None):
        node = self.cache[key]
        assert node.val[0] == key
        self.q.remove(node)
        if value is None:
            value = node.val[1]
        new_node = self.q.append((key, value))
        self.cache[key] = new_node
        return new_node

    """
    @param: key: An integer
    @return: An integer
    """

    def get(self, key):
        # write your code here
        if key in self.cache:
            node = self.move2tail(key)
            return node.val[1]
        else:
            return -1

    """
    @param: key: An integer
    @param: value: An integer
    @return: nothing
    """

    def set(self, key, value):
        # write your code here
        if key in self.cache:
            self.move2tail(key, value)
        else:
            if len(self.q) == self.cap:
                node = self.q.popleft()
                del self.cache[node.val[0]]
            node = self.q.append((key, value))
            self.cache[key] = node

还有单链表的做法：

如下(单链表)：

class LinkedNode:
    
    def __init__(self, key=None, value=None, next=None):
        self.key = key
        self.value = value
        self.next = next

class LRUCache:

    # @param capacity, an integer
    def __init__(self, capacity):
        self.key_to_prev = {}
        self.dummy = LinkedNode()
        self.tail = self.dummy
        self.capacity = capacity
    
    def push_back(self, node):
        self.key_to_prev[node.key] = self.tail
        self.tail.next = node
        self.tail = node
    
    def pop_front(self):
        # 删除头部
        head = self.dummy.next
        del self.key_to_prev[head.key]
        self.dummy.next = head.next
        self.key_to_prev[head.next.key] = self.dummy
        
    # change "prev->node->next...->tail"
    # to "prev->next->...->tail->node"
    def kick(self, prev):    #将数据移动至尾部
        node = prev.next
        if node == self.tail:
            return
        
        # remove the current node from linked list
        prev.next = node.next
        # update the previous node in hash map
        self.key_to_prev[node.next.key] = prev
        node.next = None

        self.push_back(node)

    # @return an integer
    def get(self, key):		#获取数据
        if key not in self.key_to_prev:
            return -1
        self.kick(self.key_to_prev[key])
        return self.key_to_prev[key].next.value

    # @param key, an integer
    # @param value, an integer
    # @return nothing
    def set(self, key, value):     #数据放入缓存
        if key in self.key_to_prev:	   
            self.kick(self.key_to_prev[key])
            self.key_to_prev[key].next.value = value
        	return
        
        self.push_back(LinkedNode(key, value))  #如果key不存在，则存入新节点
        if len(self.key_to_prev) > self.capacity:		#如果缓存超出上限
            self.pop_front()					#删除头部

960. 数据流中第一个独特的数 II

样例

例1:

输入:
add(1)
add(2)
firstUnique()
add(1)
firstUnique()
输出:
[1,2]

例2:

输入:
add(1)
add(2)
add(3)
add(4)
add(5)
firstUnique()
add(1)
firstUnique()
add(2)
firstUnique()
add(3)
firstUnique()
add(4)
firstUnique()
add(5)
add(6)
firstUnique()
输出:
[1,2,3,4,5,6]

657. Insert Delete GetRandom O(1)

样例

// 初始化空集set
RandomizedSet randomSet = new RandomizedSet();

// 1插入set中。返回正确因为1被成功插入
randomSet.insert(1);

// 返回错误因为2不在set中
randomSet.remove(2);

// 2插入set中，返回正确，set现在有[1,2]。
randomSet.insert(2);

// getRandom 应该随机的返回1或2。
randomSet.getRandom();

// 从set中移除1，返回正确。set现在有[2]。
randomSet.remove(1);

// 2已经在set中，返回错误。
randomSet.insert(2);

// 因为2是set中唯一的数字，所以getRandom总是返回2。
randomSet.getRandom();

使用数组来保存当前集合中的元素，同时用一个hashMap来保存数字与它在数组中下标的对应关系。

插入操作时：

若已存在此元素返回false
不存在时将新的元素插入数组最后一位，同时更新hashMap。

删除操作时：

若不存在此元素返回false
存在时先根据hashMap得到要删除数字的下标，再将数组的最后一个数放到需要删除的数的位置上，删除数组最后一位，同时更新hashMap。

获取随机数操作时：

根据数组的长度来获取一个随机的下标，再根据下标获取元素。

from random import randint

class RandomizedSet:
    
    def __init__(self):
        # do intialization if necessary
        self.pos_map = {}
        self.elements = []
        self.size = 0

    """
    @param: val: a value to the set
    @return: true if the set did not already contain the specified element or false
    """
    def insert(self, val):
        # write your code here
        if val in self.pos_map:
            return True
        if len(self.elements) == self.size:
            self.elements.append(val)
        else:
            self.elements[self.size] = val
        self.pos_map[val] = self.size
        self.size += 1
        return False

    """
    @param: val: a value from the set
    @return: true if the set contained the specified element or false
    """
    def remove(self, val):
        # write your code here
        if val not in self.pos_map:
            return False
        pos = self.pos_map[val]
        del self.pos_map[val]
        last_element = self.elements[self.size-1]
        self.elements[pos] = last_element
        self.pos_map[last_element] = pos
        self.size -= 1
        return True
   

    """
    @return: Get a random element from the set
    """
    def getRandom(self):
        # write your code here
        return self.elements[randint(0, self.size-1)]

# Your RandomizedSet object will be instantiated and called as such:
# obj = RandomizedSet()
# param = obj.insert(val)
# param = obj.remove(val)
# param = obj.getRandom()

当然，使用self.nums.pop()也可以，就不用再记录size了。

如果是非重复元素，

954. Insert Delete GetRandom O(1) - 允许重复

样例

样例 1:

输入:
insert(1)
insert(1)
insert(2)
getRandom()
remove(1)

// 初始化一个空的容器
RandomizedCollection collection = new RandomizedCollection();

// 把 1 插入到这容器中。如果这个容器不含 1 则返回 true 
collection.insert(1);

// 把 1 插入到这容器中。如果这个容器含 1 则返回 false, 此时容器中含有 [1,1]。
collection.insert(1);

// 把 1 插入到这容器中， 返回 true, 此时容器中含有 [1,1,2].
collection.insert(2);

// getRandom 应该有 2/3 的概率返回 1 ，1/3 的概率返回 2。
collection.getRandom();

// 从容器中删去一个 1 ， 此时容器中含有 [1,2].
collection.remove(1);

// getRandom 应该可以同等概率的返回 1 和 2。
collection.getRandom();

样例 2:

输入:
insert(1)
insert(1)
getRandom()
remove(1)

注意事项

允许有重复元素

则：

基本算法是不变的，只不过需要一个办法来处理重复的数。
这里的解决办法是，用 HashMap 存储 number to a list of indices in numbers array. 也就是说，把某个数在数组中出现的所有的位置用 List 的形式存储下来
这样子的话，删除一个数的时候，就是从这个 list 里随便拿走一个数（比如最后一个数）
但是还需要解决的问题是，原来的算法中，删除一个数的时候，需要拿 number array 的最后个位置的数，来覆盖掉被删除的数。那这样原本在最后一个位置的数，他在 HashMap 里的记录就应该相应的变化。
但是，我们只能得到这个移动了的数是什么，而这个被移动过的数，可能出现在好多个位置上，去要从 HashMap 里得到的 indices 列表里，改掉那个 index=当前最后一个位置的下标。
所以这里的做法是，修改 number array，不只是存储 Number，同时存储，这个数在 HashMap 的 indices 列表中是第几个数。这样就能直接去改那个数的值了。否则还得 for 循环一次，就无法做到 O(1)

import random
import collections


class RandomizedCollection(object):

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.elements = []
        self.indexes = collections.defaultdict(set)
        

    def insert(self, val):
        """
        Inserts a value to the collection. Returns true if the collection did not already contain the specified element.
        :type val: int
        :rtype: bool
        """
        self.elements.append(val)
        ans = False
        if val in self.indexes:
            ans = True
        self.indexes[val].add(len(self.elements)-1)
        return ans

    """
    just choose one element in set data
    """
    def choose_one(self, set_data):
        for i in set_data:
            return i
    
    
    def remove(self, val):
        """
        Removes a value from the collection. Returns true if the collection contained the specified element.
        :type val: int
        :rtype: bool
        """
        if val in self.indexes and self.indexes[val]:
            last_pos = len(self.elements)-1
            last_element = self.elements[last_pos]
            assert last_pos in self.indexes[last_element]
            self.indexes[last_element].remove(last_pos)
            
            if val != last_element:
                pos = self.choose_one(self.indexes[val])
                self.indexes[last_element].add(pos)
                self.indexes[val].remove(pos)
                self.elements[pos] = last_element
            self.elements.pop()
            return True
        else:
            return False
        

    def getRandom(self):
        """
        Get a random element from the collection.
        :rtype: int
        """
        return self.elements[random.randint(0, len(self.elements)-1)]
        


# Your RandomizedCollection object will be instantiated and called as such:
# obj = RandomizedCollection()
# param_1 = obj.insert(val)
# param_2 = obj.remove(val)
# param_3 = obj.getRandom()

哈希表 Hash

哈希表（Java 中的 HashSet / HashMap，C++ 中的 unordered_map，Python 中的 dict）是面试中非常常见的数据结构。它的主要考点有两个：

是否会灵活的使用哈希表解决问题
是否熟练掌握哈希表的基本原理

这一小节中，我们将介绍一下哈希表原理中的几个重要的知识点：

哈希表的工作原理
为什么 hash 上各种操作的时间复杂度不能单纯的认为是 O(1) 的
哈希函数（Hash Function）该如何实现
哈希冲突（Collision）该如何解决
如何让哈希表可以不断扩容？

在数据结构中，哈希函数是用来将一个字符串（或任何其他类型）转化为小于哈希表大小且大于等于零的整数。一个好的哈希函数可以尽可能少地产生冲突。一种广泛使用的哈希函数算法是使用数值33，假设任何字符串都是基于33的一个大整数，比如：

hashcode("abcd") = (ascii(a) * 333 + ascii(b) * 332 + ascii(c) *33 + ascii(d)) % HASH_SIZE

= (97* 333 + 98 * 332 + 99 * 33 +100) % HASH_SIZE

= 3595978 % HASH_SIZE

其中HASH_SIZE表示哈希表的大小(可以假设一个哈希表就是一个索引0 ~ HASH_SIZE-1的数组)。

给出一个字符串作为key和一个哈希表的大小，返回这个字符串的哈希值。

在线评测地址: http://www.lintcode.com/problem/hash-function/

class Solution:
    """
    @param key: A String you should hash
    @param HASH_SIZE: An integer
    @return an integer
    """
    def hashCode(self, key, HASH_SIZE):
        # write your code here
        ans = 0
        for x in key:
            ans = (ans * 33 + ord(x)) % HASH_SIZE
        return ans

　　取模过程要使用同余定理：
(a * b ) % MOD = ((a % MOD) * (b % MOD)) % MOD

冲突（Collision），是说两个不同的 key 经过哈希函数的计算后，得到了两个相同的值。解决冲突的方法，主要有两种：

开散列法（Open Hashing）。是指哈希表所基于的数组中，每个位置是一个 Linked List 的头结点。这样冲突的 <key, value> 二元组，就都放在同一个链表中。
闭散列法（Closed Hashing）。是指在发生冲突的时候，后来的元素，往下一个位置去找空位。

哈希表容量的大小在一开始是不确定的。如果哈希表存储的元素太多（如超过容量的十分之一），我们应该将哈希表容量扩大一倍，并将所有的哈希值重新安排。假设你有如下一哈希表：

size=3, capacity=4

[null, 21, 14, null]
       ↓    ↓
       9   null
       ↓
      null

哈希函数为：

int hashcode(int key, int capacity) {
    return key % capacity;
}

这里有三个数字9，14，21，其中21和9共享同一个位置因为它们有相同的哈希值1(21 % 4 = 9 % 4 = 1)。我们将它们存储在同一个链表中。

重建哈希表，将容量扩大一倍，我们将会得到：

size=3, capacity=8

index:   0    1    2    3     4    5    6   7
hash : [null, 9, null, null, null, 21, 14, null]

给定一个哈希表，返回重哈希后的哈希表。

在线评测地址: http://www.lintcode.com/problem/rehashing/

class Solution:
    def addlistnode(self, node, number):
        if node.next != None:
            self.addlistnode(node.next, number)
        else:
            node.next = ListNode(number)

    def addnode(self, anshashTable, number):
        p = number % len(anshashTable)
        if anshashTable[p] == None:
            anshashTable[p] = ListNode(number)
        else:
            self.addlistnode(anshashTable[p], number)

    def rehashing(self,hashTable):
        HASH_SIZE = 2 * len(hashTable)
        anshashTable = [None for i in range(HASH_SIZE)]
        for item in hashTable:
            p = item
            while p != None:
                self.addnode(anshashTable,p.val)
                p = p.next
        return anshashTable

138. 子数组之和

注意事项

至少有一个子数组的和为 0

用前缀和某一段[l, r]的和为0，则其对应presum[l-1] = presum[r].
presum 为数组前缀和。只要保存每个前缀和，找是否有相同的前缀和即可。

class Solution:
    """
    @param nums: A list of integers
    @return: A list of integers includes the index of the first number and the index of the last number
    """
    def subarraySum(self, nums):
        prefix_hash = {0: -1}
        prefix_sum = 0
        for i, num in enumerate(nums):
            prefix_sum += num
            if prefix_sum in prefix_hash:
                return prefix_hash[prefix_sum]+1, i
            prefix_hash[prefix_sum] = i
            
        return -1, -1

i-1, 出错？？？没有搞懂。

105. 复制带随机指针的链表

挑战

可否使用O(1)的空间

"""
Definition for singly-linked list with a random pointer.
class RandomListNode:
    def __init__(self, x):
        self.label = x
        self.next = None
        self.random = None
"""


class Solution:
    # @param head: A RandomListNode
    # @return: A RandomListNode
    def copyRandomList(self, head):
        # write your code here
        if not head:
            return None
        copied_head, map_nodes = self.copy_nodes(head)
        self.copy_link(head, map_nodes)
        return copied_head
    
    def copy_nodes(self, head):
        dummy = RandomListNode(None) # Tips
        node, pre = head, dummy
        map_nodes = {}
        while node:
            node_cp = RandomListNode(node.label)
            map_nodes[node] = node_cp
            pre.next = node_cp
            node = node.next
            pre = node_cp
        return dummy.next, map_nodes
    
    def copy_link(self, head, map_nodes):
        node = head
        while node:
            if node.random:
                map_nodes[node].random = map_nodes[node.random]
            node = node.next

124. 最长连续序列

说明

要求你的算法复杂度为O(n)

class Solution:
    """
    @param num: A list of integers
    @return: An integer
    """

    def longestConsecutive(self, num):
        # write your code here
        ans = 1
        uniq_num_visted = {n: False for n in num}
        for n in uniq_num_visted:
            if uniq_num_visted[n]:
                continue

            uniq_num_visted[n] = True
            while n + 1 in uniq_num_visted:
                uniq_num_visted[n + 1] = True
                n += 1
            high = n

            while n - 1 in uniq_num_visted:
                uniq_num_visted[n - 1] = True
                n -= 1
            low = n
            ans = max(ans, high-low+1)

        return ans

Heap 的结构和原理

基于 Siftup 的版本

Python版本：

import sys
import collections
class Solution:
    # @param A: Given an integer array
    # @return: void
    def  siftup(self, A, k):
        while k != 0:
            father = (k - 1) // 2
            if A[k] > A[father]:
                break
            temp = A[k]
            A[k] = A[father]
            A[father] = temp
            
            k = father
    def heapify(self, A):
        for i in range(len(A)):
            self.siftup(A, i)

算法思路：

对于每个元素A[i]，比较A[i]和它的父亲结点的大小，如果小于父亲结点，则与父亲结点交换。
交换后再和新的父亲比较，重复上述操作，直至该点的值大于父亲。

时间复杂度分析

对于每个元素都要遍历一遍，这部分是
每处理一个元素时，最多需要向根部方向交换

因此总的时间复杂度是

基于 Siftdown 的版本

Python版本：

import sys
import collections
class Solution:
    # @param A: Given an integer array
    # @return: void
    def siftdown(self, A, k):
        while k * 2 + 1 < len(A):
            son = k * 2 + 1    #A[i]左儿子的下标
            if k * 2 + 2 < len(A) and A[son] > A[k * 2 + 2]:
                son = k * 2 + 2    #选择两个儿子中较小的一个
            if A[son] >= A[k]:
                break
                
            temp = A[son]
            A[son] = A[k]
            A[k] = temp
            k = son
    
    def heapify(self, A):
        for i in range(len(A) - 1, -1, -1):
            self.siftdown(A, i)

算法思路：

初始选择最接近叶子的一个父结点，与其两个儿子中较小的一个比较，若大于儿子，则与儿子交换。
交换后再与新的儿子比较并交换，直至没有儿子。
再选择较浅深度的父亲结点，重复上述步骤。

时间复杂度分析

这个版本的算法，乍一看也是

T(n) = O(n/4) + O(n/8 * 2) + O(n/16 * 3) ...

然后我们用 2T - T 得到：

2 * T(n) = O(n/2) + O(n/4 * 2) + O(n/8 * 3) + O(n/16 * 4) ... 
T(n)     =          O(n/4)     + O(n/8 * 2) + O(n/16 * 3) ...

2 * T(n) - T(n) = O(n/2) +O (n/4) + O(n/8) + ...
                = O(n/2 + n/4 + n/8 + ... )
                = O(n)

因此得到 T(n) = 2 * T(n) - T(n) = O(n)

红黑树（Red-black Tree）是一种平衡排序二叉树（Balanced Binary Search Tree），在它上面进行增删查改的平均时间复杂度都是

Q: 在面试中考不考呢？
A: 很少考……

Q: 需不需要了解呢？
A: 需要！

Q: 了解到什么程度呢？
A: 知道它是 Balanced Binary Search Tree，知道它支持什么样的操作，会用就行。不需要知道具体的实现原理。

红黑树的几个常用操作

Java当中，红黑树主要是TreeSet，位于java.util.TreeSet，继承自java.util.AbstractSet，它的主要方法有：

add，插入一个元素。
remove，删除一个元素。
clear，删除所有元素。
contains，查找是否包含某元素。
isEmpty，是否空树。
size，返回元素个数。
iterator，返回迭代器。
clone，对整棵树进行浅拷贝，即不拷贝元素本身。
first，返回最前元素。
last，返回最末元素。
floor，返回不大于给定元素的最大元素。
ceiling，返回不小于给定元素的最小元素。
pollFirst，删除并返回首元素。
pollLast，删除并返回末元素。

更具体的细节，请参考Java Reference。

此外，在Java当中，有一种map，用红黑树实现key查找，这种结构叫做TreeMap。如果你需要一种map，并且它的key是有序的，那么强烈推荐TreeMap。

在C++当中，红黑树即是默认的set和map，其元素也是有序的。
而通过哈系表实现的则分别是unordered_set和unordered_map，注意这两种结构是在C++11才有的。
在Python当中，默认的set和dict是用哈系表实现，没有默认的红黑树。如果你想使用红黑树的话，可以使用rbtree这个模块，下载地址：https://pypi.python.org/pypi/rbtree/0.9.0

Merge K Sorted Lists 多路归并算法的三种实现方式

外排序与K路归并算法

介绍

外排序算法（External Sorting），是指在内存不够的情况下，如何对存储在一个或者多个大文件中的数据进行排序的算法。外排序算法通常是解决一些大数据处理问题的第一个步骤，或者是面试官所会考察的算法基本功。外排序算法是海量数据处理算法中十分重要的一块。
在学习这类大数据算法时，经常要考虑到内存、缓存、准确度等因素，这和我们之前见到的算法都略有差别。

基本步骤

外排序算法分为两个基本步骤：

将大文件切分为若干个个小文件，并分别使用内存排好序
使用K路归并算法（k-way merge）将若干个排好序的小文件合并到一个大文件中

第一步：文件拆分

根据内存的大小，尽可能多的分批次的将数据 Load 到内存中，并使用系统自带的内存排序函数（或者自己写个快速排序算法），将其排好序，并输出到一个个小文件中。比如一个文件有1T，内存有1G，那么我们就这个大文件中的内容按照 1G 的大小，分批次的导入内存，排序之后输出得到 1024 个 1G 的小文件。

第二步：K路归并算法

K路归并算法使用的是数据结构堆（Heap）来完成的，使用 Java 或者 C++ 的同学可以直接用语言自带的 PriorityQueue（C++中叫priority_queue）来代替。

我们将 K 个文件中的第一个元素加入到堆里，假设数据是从小到大排序的话，那么这个堆是一个最小堆（Min Heap）。每次从堆中选出最小的元素，输出到目标结果文件中，然后如果这个元素来自第 x 个文件，则从第 x 个文件中继续读入一个新的数进来放到堆里，并重复上述操作，直到所有元素都被输出到目标结果文件中。

Follow up: 一个个从文件中读入数据，一个个输出到目标文件中操作很慢，如何优化？

如果我们每个文件只读入1个元素并放入堆里的话，总共只用到了 1024 个元素，这很小，没有充分的利用好内存。另外，单个读入和单个输出的方式也不是磁盘的高效使用方式。因此我们可以为输入和输出都分别加入一个缓冲（Buffer）。假如一个元素有10个字节大小的话，1024 个元素一共 10K，1G的内存可以支持约 100K 组这样的数据，那么我们就为每个文件设置一个 100K 大小的 Buffer，每次需要从某个文件中读数据，都将这个 Buffer 装满。当然 Buffer 中的数据都用完的时候，再批量的从文件中读入。输出同理，设置一个 Buffer 来避免单个输出带来的效率缓慢。

将者，智、信、仁、勇、严也。

Hi，我是李智华，华为-安全AI算法专家，欢迎来到安全攻防对抗的有趣世界。

栈队列 hash表堆算法模板和相关题目

什么是栈（Stack）？

如何自己实现一个栈？

栈在计算机内存当中的应用

队列

定义

思路

示例代码

什么是循环数组，如何用循环数组实现队列？

什么是循环数组

如何实现队列

示例代码

在线练习

642. 数据流滑动窗口平均值

哈希表 Hash

138. 子数组之和

Heap 的结构和原理

基于 Siftup 的版本

时间复杂度分析

基于 Siftdown 的版本

时间复杂度分析

红黑树的几个常用操作

Merge K Sorted Lists 多路归并算法的三种实现方式

外排序与K路归并算法

介绍

基本步骤

第一步：文件拆分

第二步：K路归并算法

Follow up: 一个个从文件中读入数据，一个个输出到目标文件中操作很慢，如何优化？

相关练习

378. 有序矩阵中第 K 小的元素

公告

将者，智、信、仁、勇、严也。

Hi，我是李智华，华为-安全AI算法专家，欢迎来到安全攻防对抗的有趣世界。

栈 队列 hash表 堆 算法模板和相关题目

什么是栈（Stack）？

如何自己实现一个栈？

栈在计算机内存当中的应用

队列

定义

思路

示例代码

什么是循环数组，如何用循环数组实现队列？

什么是循环数组

如何实现队列

示例代码

在线练习

642. 数据流滑动窗口平均值

样例

134. LRU缓存策略

样例

960. 数据流中第一个独特的数 II

样例

注意事项

657. Insert Delete GetRandom O(1)

样例

954. Insert Delete GetRandom O(1) - 允许重复

样例

注意事项

哈希表 Hash

138. 子数组之和

样例

注意事项

105. 复制带随机指针的链表

挑战

124. 最长连续序列

样例

说明

Heap 的结构和原理

基于 Siftup 的版本 O(nlogn)

时间复杂度分析

基于 Siftdown 的版本 O(n)

时间复杂度分析

红黑树的几个常用操作

Merge K Sorted Lists 多路归并算法的三种实现方式

外排序与K路归并算法

介绍

基本步骤

第一步：文件拆分

第二步：K路归并算法

Follow up: 一个个从文件中读入数据，一个个输出到目标文件中操作很慢，如何优化？

相关练习

378. 有序矩阵中第 K 小的元素

公告

栈队列 hash表堆算法模板和相关题目

基于 Siftup 的版本

基于 Siftdown 的版本