BFS (1)算法模板 看是否需要分层 （2）拓扑排序——检测编译时的循环依赖 制定有依赖关系的任务的执行顺序

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
BFS模板，记住这5个：
（1）针对树的BFS
1.1 无需分层遍历
    from collections import deque
     
    def levelOrderTree(root):
        if not root:
            return
              
        q = deque([root])
        while q:
            head = q.popleft()
            do something with this head node...
            if head.left:               
                q.append(head.left)
            if head.right:
                q.append(head.right)               
        return xxx
1.2 需要分层遍历
    def levelOrderTree(root):
        if not root:
            return
                  
        q = [root]
        while q:
            new_q = []
            for node in q: # 和上面代码相比 差异就在这里 和 deque
                do something with this layer nodes...
                if node.left:
                    new_q.append(node.left)
                if node.right:
                    new_q.append(node.right)           
            q = new_q
        return xxx
         
（2）针对图的BFS
2.1 无需分层遍历
  from collections import deque
   
  def bfs_graph(root): 
    if not root:
        return
     
    queue = deque([root])
    seen = set([root]) 
    while queue:
        head = queue.popleft()
        do something with this head...
        for neighbor in head.neighbors:
            if neighbor not in seen: # 和tree的区别无非就是多了一个是否访问过的判断
                seen.add(neighbor)
                queue.append(neighbor)
　　return xxx
 
上述代码中：
neighbor 表示从某个点 head 出发，可以走到的下一层的节点。
set/seen 存储已经访问过的节点（已经丢到 queue 里去过的节点）
queue 存储等待被拓展到下一层的节点
set/seen 与 queue 是一对好基友，无时无刻都一起出现，往 queue 里新增一个节点，就要同时丢到 set 里。
需要分层遍历的宽度搜先搜索
 
2.2 需分层遍历【较为少见，可以先不看】
 
    def bfs_graph(root):
        if not root:
            return []
                  
        q = [root]
        seen = set([root])
        while q:
            new_q = []
            for node in q:
                do something with this layer nodes...              
                for neighbor in node.neighbors:
                    if neighbor not in seen: # 和tree的区别无非就是多了一个是否访问过的判断
                        seen.add(neighbor)
                        new_q.append(neighbor)          
            q = new_q
        return xxx
 
 
（3）拓扑排序 ==》仅仅针对有向无环图，！！！如果是有环的图，则生成的排序仅仅能够完成无环的点，有环路的点因为入度始终无法为0，所以不会加入到排序结果！==》体会精髓！！！
<br>更新代码模板：20230208 果然还是比我的简洁        q = [u for u, d in inDeg.items() if d == 0]
        for u in q:
            for v in g[u]:
                inDeg[v] -= 1
                if inDeg[v] == 0:
                    q.append(v)
        return q
之前的模板<br>
记住下面的代码
class Solution:
    """
    @param graph: A list of Directed graph node
    @return: Any topological order for the given graph.
    """
    def topSort(self, graph):
        node_to_indegree = self.get_indegree(graph)
  
        # bfs
        order = []
        start_nodes = [n for n in graph if node_to_indegree[n] == 0]
        queue = collections.deque(start_nodes)
        while queue:
            node = queue.popleft()
            order.append(node)
            for neighbor in node.neighbors:
                node_to_indegree[neighbor] -= 1
                if node_to_indegree[neighbor] == 0:
                    queue.append(neighbor)
                  
        return order
      
    def get_indegree(self, graph):
        node_to_indegree = {x: 0 for x in graph}
  
        for node in graph:
            for neighbor in node.neighbors:
                node_to_indegree[neighbor] += 1
                  
        return node_to_indegree
 
算法流程
拓扑排序的算法是典型的宽度优先搜索算法，其大致流程如下：
统计所有点的入度，并初始化拓扑序列为空。
将所有入度为 0 的点，也就是那些没有任何依赖的点，放到宽度优先搜索的队列中
将队列中的点一个一个的释放出来，放到拓扑序列中，每次释放出某个点 A 的时候，就访问 A 的相邻点（所有A指向的点），并把这些点的入度减去 1。
如果发现某个点的入度被减去 1 之后变成了 0，则放入队列中。
直到队列为空时，算法结束       
 
 
一些实际案例：
https://www.cnblogs.com/bonelee/p/11724346.html

　　

　　

外加一个djstra最短路算法：

 下面示例求解最短的飞行航线

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from heapq import heappush, heappop
 
 
def dijkstra(graph, from_node, to_node):
    q = [(0, from_node, [])]
    seen = {from_node}
    while q:
        cost, node, path = heappop(q)
        path = path + [node]
 
        if node == to_node:
            return cost, path
 
        for adj_node, c in graph.get(node, {}).items():
            if adj_node not in seen:
                seen.add(adj_node)
                heappush(q, (cost + c, adj_node, path))
 
    return -1, []
 
 
air_lines = {"1": {"2": 2000, "3": 2000, "4": 4000, "5": 4500}, "2": {"5": 1000}, "3": {"4": 1000}, "4": {"5": 500}}
 
print(dijkstra(air_lines, "1", "4"))
print(dijkstra(air_lines, "1", "5"))
print(dijkstra(air_lines, "4", "5"))
print(dijkstra(air_lines, "5", "4"))
print(dijkstra(air_lines, "1", "1"))
print(dijkstra(air_lines, "10", "10"))

　==》上面代码有问题，下面这个才是ok的！因为1,4返回了4000的结果，其实是3000！理由是4再第一次加入队列以后再也没有机会更新了！实际上，134路径还应该有更新的机会：　

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from heapq import heappush, heappop
 
 
def dijkstra(graph, from_node, to_node):
    q, seen = [(0, from_node, [])], set()
    while q:
        cost, node, path = heappop(q)
        seen.add(node)
        path = path + [node]
 
        if node == to_node:
            return cost, path
 
        for adj_node, c in graph.get(node, {}).items():
            if adj_node not in seen:
                heappush(q, (cost + c, adj_node, path))
 
    return -1, []
 
 
air_lines = {"1": {"2": 2000, "3": 2000, "4": 4000, "5": 4500}, "2": {"5": 1000}, "3": {"4": 1000}, "4": {"5": 500}}
 
print(dijkstra(air_lines, "1", "4"))
print(dijkstra(air_lines, "1", "5"))
print(dijkstra(air_lines, "4", "5"))
print(dijkstra(air_lines, "5", "4"))
print(dijkstra(air_lines, "1", "1"))
print(dijkstra(air_lines, "10", "10"))　

发现bfs和dfs都搞不定的时候，大概率要用这个！

====》上面的模板有问题，因为没有最短距离的松弛，见文末的代码！！！

 

69. 二叉树的层次遍历

中文English

给出一棵二叉树，返回其节点值的层次遍历（逐层从左往右访问）

Example

样例 1:

输入：{1,2,3}
输出：[[1],[2,3]]
解释：
   1
  / \
 2   3
它将被序列化为{1,2,3}
层次遍历

样例 2:

输入：{1,#,2,3}
输出：[[1],[2],[3]]
解释：
1
 \
  2
 /
3
它将被序列化为{1,#,2,3}
层次遍历

Challenge

挑战1：只使用一个队列去实现它

挑战2：用BFS算法来做

Notice

  • 首个数据为根节点，后面接着是其左儿子和右儿子节点值，"#"表示不存在该子节点。
  • 节点数量不超过20。
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
"""
Definition of TreeNode:
class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left, self.right = None, None
"""
 
 
class Solution:
    """
    @param root: A Tree
    @return: Level order a list of lists of integer
    """
    def levelOrder(self, root):
        # write your code here
        if not root:
            return []
             
        q = [root]
        result = []
        while q:
            children = []
            q2 = []
            for node in q:
                children.append(node.val)
                if node.left:
                    q2.append(node.left)
                if node.right:   
                    q2.append(node.right)
            result.append(children)
            q = q2
        return result
                

 

71. 二叉树的锯齿形层次遍历

中文
English

给出一棵二叉树，返回其节点值的锯齿形层次遍历（先从左往右，下一层再从右往左，层与层之间交替进行） 

样例

样例 1:

输入:{1,2,3}
输出:[[1],[3,2]]
解释:
    1
   / \
  2   3
它将被序列化为 {1,2,3}

样例 2:

输入:{3,9,20,#,#,15,7}
输出:[[3],[20,9],[15,7]]
解释:
    3
   / \
  9  20
    /  \
   15   7
它将被序列化为 {3,9,20,#,#,15,7}
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
"""
Definition of TreeNode:
class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left, self.right = None, None
"""
 
class Solution:
    """
    @param root: A Tree
    @return: A list of lists of integer include the zigzag level order traversal of its nodes' values.
    """
    def zigzagLevelOrder(self, root):
        # write your code here
        if not root:
            return []
         
        q = [root]
        result = []
        layer = 0
        while q:
            q2 = []
            values = []
            for node in q:
                values.append(node.val)
                if node.left:
                    q2.append(node.left)
                if node.right:
                    q2.append(node.right)
            if layer % 2 == 0:
                result.append(values)
            else:
                result.append(values[::-1])
            q = q2
            layer += 1
        return result
                

 

70. 二叉树的层次遍历 II

中文
English

给出一棵二叉树，返回其节点值从底向上的层次序遍历（按从叶节点所在层到根节点所在的层遍历，然后逐层从左往右遍历）

样例

例1:

输入:
{1,2,3}
输出:
[[2,3],[1]]
解释:
    1
   / \
  2   3
它将被序列化为 {1,2,3}
层次遍历

例2:

输入:
{3,9,20,#,#,15,7}
输出:
[[15,7],[9,20],[3]]
解释:
    3
   / \
  9  20
    /  \
   15   7
它将被序列化为 {3,9,20,#,#,15,7}
层次遍历
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
"""
Definition of TreeNode:
class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left, self.right = None, None
"""
 
class Solution:
    """
    @param root: A tree
    @return: buttom-up level order a list of lists of integer
    """
    def levelOrderBottom(self, root):
        # write your code here
        # write your code here
        if not root:
            return []
         
        result = []
        q = [root]
        while q:
            new_q = []
            values = []
            for node in q:
                values.append(node.val)
                if node.left:
                    new_q.append(node.left)
                if node.right:
                    new_q.append(node.right)
            result.append(values)
            q = new_q
        return result[::-1]

 

 

137. 克隆图

中文
English

克隆一张无向图. 无向图的每个节点包含一个 label 和一个列表 neighbors. 保证每个节点的 label 互不相同.

你的程序需要返回一个经过深度拷贝的新图. 新图和原图具有同样的结构, 并且对新图的任何改动不会对原图造成任何影响.

样例

样例1

输入:
{1,2,4#2,1,4#4,1,2}
输出: 
{1,2,4#2,1,4#4,1,2}
解释:
1------2  
 \     |  
  \    |  
   \   |  
    \  |  
      4

说明

关于无向图的表示: http://www.lintcode.com/help/graph/

注意事项

你需要返回与给定节点具有相同 label 的那个节点.

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
"""
Definition for a undirected graph node
class UndirectedGraphNode:
    def __init__(self, x):
        self.label = x
        self.neighbors = []
"""
 
from collections import deque
 
 
class Solution:
    """
    @param: node: A undirected graph node
    @return: A undirected graph node
    """
    def cloneGraph(self, root):
        # write your code here
        if not root:
            return None
         
        """
        使用宽度优先搜索 BFS 的版本。
        第一步：找到所有独一的点
        第二步：复制所有的点，将映射关系存起来
        第三步：找到所有的边，复制每一条边
        """
        nodes = self.get_unique_nodes(root)
        mapping_nodes = self.copy_nodes(nodes)
        self.copy_edges(nodes, mapping_nodes)
        return mapping_nodes[root]
         
     
    def get_unique_nodes(self, root):
        q, seen = deque([root]), set([root])
        while q:
            node = q.popleft()
            for neighbor_node in node.neighbors:
                if neighbor_node not in seen:
                    seen.add(neighbor_node)
                    q.append(neighbor_node)
        return seen
     
     
    def copy_nodes(self, nodes):
        return {node: UndirectedGraphNode(node.label) for node in nodes}
     
     
    def copy_edges(self, nodes, mapping_nodes):
        for node in nodes:
            copied_node = mapping_nodes[node]
            for neighbor in node.neighbors:
                copied_node.neighbors.append(mapping_nodes[neighbor])
                

 

120. 单词接龙

中文
English

给出两个单词（start和end）和一个字典，找出从start到end的最短转换序列，输出最短序列的长度。

变换规则如下：

  1. 每次只能改变一个字母。
  2. 变换过程中的中间单词必须在字典中出现。(起始单词和结束单词不需要出现在字典中)

样例

样例 1:

输入：start = "a"，end = "c"，dict =["a","b","c"]
输出：2
解释：
"a"->"c"

样例 2:

输入：start ="hit"，end = "cog"，dict =["hot","dot","dog","lot","log"]
输出：5
解释：
"hit"->"hot"->"dot"->"dog"->"cog"

注意事项

  • 如果不存在这样的转换序列，返回 0。
  • 所有单词具有相同的长度。
  • 所有单词只由小写字母组成。
  • 字典中不存在重复的单词。
  • 你可以假设 beginWord 和 endWord 是非空的，且二者不相同。
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution:
    """
    @param: start: a string
    @param: end: a string
    @param: dict: a set of string
    @return: An integer
    """
    def ladderLength(self, start, end, dict):
        dict.add(end)
        q = [start]
        visited = set([start])
         
        distance = 0
        while q:
            distance += 1
            new_q = []
            for word in q:
                if word == end:
                    return distance
                 
                for next_word in self.get_next_words(word):
                    if next_word not in dict or next_word in visited:
                        continue
                    new_q.append(next_word)
                    visited.add(next_word)
            q = new_q
 
        return 0
         
    # O(26 * L^2)
    # L is the length of word
    def get_next_words(self, word):
        words = []
        for i in range(len(word)):
            left, right = word[:i], word[i + 1:]
            for char in 'abcdefghijklmnopqrstuvwxyz':
                if word[i] == char:
                    continue
                words.append(left + char + right)
        return words       

 

我用dijstra算法求解如下：优势是可以找到最短的路径！！！

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from typing import (
    Set,
)
import heapq
 
 
class Solution:
    """
    @param start: a string
    @param end: a string
    @param dict: a set of string
    @return: An integer
    """
    def ladder_length(self, start: str, end: str, wdict: Set[str]) -> int:
        # write your code here       
        q = [(1, start, [start])]
        seen = {start}
        wdict.add(end)
 
        while q:
            cost, virtex, path = heapq.heappop(q)           
            if virtex == end:
                print(path)
                return cost
 
            neibors = self.get_neibors(virtex, wdict)              
            for neibor in neibors:                
                if neibor not in seen:
                    seen.add(neibor)
                    heapq.heappush(q, (cost + 1, neibor, path+[neibor]))
 
    def get_neibors(self, word, words_set):
        words = []
        for i in range(len(word)):
            left, right = word[:i], word[i + 1:]
            for char in 'abcdefghijklmnopqrstuvwxyz':
                if word[i] == char:
                    continue
                 
                word2 = left + char + right              
                if word2 in words_set:                   
                    words.append(word2)
        return words    

 

https://leetcode.cn/problems/remove-invalid-parentheses/ 类似上面word变换

301. 删除无效的括号

给你一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。

返回所有可能的结果。答案可以按 任意顺序 返回。

 

示例 1：

输入：s = "()())()"
输出：["(())()","()()()"]

示例 2：

输入：s = "(a)())()"
输出：["(a())()","(a)()()"]

示例 3：

输入：s = ")("
输出：[""]
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def removeInvalidParentheses(self, s: str) -> List[str]:
        def isValid(s:str)->bool:
            cnt = 0
            for c in s:
                if c == "(": cnt += 1
                elif c == ")": cnt -= 1
                if cnt < 0: return False
            return cnt == 0
 
        # BFS
        level = {s}  # 用set避免重复
        while True:
            valid = list(filter(isValid, level))  # 所有合法字符都筛选出来
            if valid: return valid # 如果当前valid是非空的，说明已经有合法的产生了
            # 下一层level
            next_level = set()
            for item in level:
                for i in range(len(item)):
                    if item[i] in "()": # 如果item[i]这个char是个括号就删了，如果不是括号就留着
                        next_level.add(item[:i]+item[i+1:])
            level = next_level

 




7. 二叉树的序列化和反序列化

中文
English

设计一个算法，并编写代码来序列化和反序列化二叉树。将树写入一个文件被称为“序列化”，读取文件后重建同样的二叉树被称为“反序列化”。

如何反序列化或序列化二叉树是没有限制的，你只需要确保可以将二叉树序列化为一个字符串，并且可以将字符串反序列化为原来的树结构。

样例

样例 1：

输入：{3,9,20,#,#,15,7}
输出：{3,9,20,#,#,15,7}
解释：
二叉树 {3,9,20,#,#,15,7}，表示如下的树结构：
	  3
	 / \
	9  20
	  /  \
	 15   7
它将被序列化为 {3,9,20,#,#,15,7}

样例 2：

输入：{1,2,3}
输出：{1,2,3}
解释：
二叉树 {1,2,3}，表示如下的树结构：
   1
  / \
 2   3
它将被序列化为 {1,2,3}

我们的数据是进行 BFS 遍历得到的。当你测试结果 Wrong Answer 时，你可以作为输入调试你的代码。

你可以采用其他的方法进行序列化和反序列化。

注意事项

对二进制树进行反序列化或序列化的方式没有限制，LintCode 将您的 serialize 输出作为 deserialize 的输入，它不会检查序列化的结果。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
"""
Definition of TreeNode:
class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left, self.right = None, None
"""
 
from collections import deque
 
 
class Solution:
    """
    @param root: An object of TreeNode, denote the root of the binary tree.
    This method will be invoked first, you should design your own algorithm
    to serialize a binary tree which denote by a root node to a string which
    can be easily deserialized by your own "deserialize" method later.
    """
    def serialize(self, root):
        # write your code here
        if not root:
            return []
             
        q = deque([root])
        result = []
        while q:
            head = q.popleft()
            if head:
                result.append(str(head.val))
                q.append(head.left)
                q.append(head.right)
            else:
                result.append('#')
                 
        while result and result[-1] == '#':
            result.pop()
             
        return result
         
 
    """
    @param data: A string serialized by your serialize method.
    This method will be invoked second, the argument data is what exactly
    you serialized at method "serialize", that means the data is not given by
    system, it's given by your own serialize method. So the format of data is
    designed by yourself, and deserialize it here as you serialize it in
    "serialize" method.
    """
    def deserialize(self, data):
        # write your code here
        if not data:
            return None
         
        root = TreeNode(data[0])
        q = deque([root])
        i = 1
        while q and i < len(data):
            head = q.popleft()
            if data[i] != '#':
                head.left = TreeNode(data[i])
                q.append(head.left)
            i += 1
            if data[i] != '#':
                head.right = TreeNode(data[i])
                q.append(head.right)
            i += 1
        return root

 

433. 岛屿的个数

中文
English

给一个 01 矩阵，求不同的岛屿的个数。

0 代表海，1 代表岛，如果两个 1 相邻，那么这两个 1 属于同一个岛。我们只考虑上下左右为相邻。

样例

样例 1：

输入：
[
  [1,1,0,0,0],
  [0,1,0,0,1],
  [0,0,0,1,1],
  [0,0,0,0,0],
  [0,0,0,0,1]
]
输出：
3

样例 2：

输入：
[
  [1,1]
]
输出：
1
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
from collections import deque
 
 
class Solution:
    """
    @param grid: a boolean 2D matrix
    @return: an integer
    """
    def numIslands(self, grid):
        if not grid or not grid[0]:
            return 0
             
        islands = 0
        visited = set()
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] and (i, j) not in visited:
                    self.bfs(grid, i, j, visited)
                    islands += 1
                     
        return islands                   
     
    def bfs(self, grid, x, y, visited):
        queue = deque([(x, y)])
        visited.add((x, y))
        while queue:
            x, y = queue.popleft()
            for delta_x, delta_y in [(1, 0), (0, -1), (-1, 0), (0, 1)]:
                next_x = x + delta_x
                next_y = y + delta_y
                if not self.is_valid(grid, next_x, next_y, visited):
                    continue
                queue.append((next_x, next_y))
                visited.add((next_x, next_y))
 
    def is_valid(self, grid, x, y, visited):
        n, m = len(grid), len(grid[0])
        if not (0 <= x < n and 0 <= y < m):
            return False
        if (x, y) in visited:
            return False
        return grid[x][y]

 

611. 骑士的最短路线

中文
English

给定骑士在棋盘上的 初始 位置(一个2进制矩阵 0 表示空 1 表示有障碍物)，找到到达 终点 的最短路线，返回路线的长度。如果骑士不能到达则返回 -1 。

样例

例1:

输入:
[[0,0,0],
 [0,0,0],
 [0,0,0]]
source = [2, 0] destination = [2, 2] 
输出: 2
解释:
[2,0]->[0,1]->[2,2]

例2:

输入:
[[0,1,0],
 [0,0,1],
 [0,0,0]]
source = [2, 0] destination = [2, 2] 
输出:-1

说明

如果骑士的位置为 (x,y)，他下一步可以到达以下这些位置:

(x + 1, y + 2)
(x + 1, y - 2)
(x - 1, y + 2)
(x - 1, y - 2)
(x + 2, y + 1)
(x + 2, y - 1)
(x - 2, y + 1)
(x - 2, y - 1)

注意事项

起点跟终点必定为空.
骑士不能碰到障碍物.
路径长度指骑士走的步数.

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
"""
Definition for a point.
class Point:
    def __init__(self, a=0, b=0):
        self.x = a
        self.y = b
"""
 
DIRECTIONS = [
    (-2, -1), (-2, 1), (-1, 2), (1, 2),
    (2, 1), (2, -1), (1, -2), (-1, -2),
]
 
class Solution:
         
    """
    @param grid: a chessboard included 0 (false) and 1 (true)
    @param source: a point
    @param destination: a point
    @return: the shortest path
    """
    def shortestPath(self, grid, source, destination):
        queue = collections.deque([(source.x, source.y)])
        distance = {(source.x, source.y): 0}
 
        while queue:
            x, y = queue.popleft()
            if (x, y) == (destination.x, destination.y):
                return distance[(x, y)]
            for dx, dy in DIRECTIONS:
                next_x, next_y = x + dx, y + dy
                if (next_x, next_y) in distance:
                    continue
                if not self.is_valid(next_x, next_y, grid):
                    continue
                distance[(next_x, next_y)] = distance[(x, y)] + 1
                queue.append((next_x, next_y))
        return -1
         
    def is_valid(self, x, y, grid):
        n, m = len(grid), len(grid[0])
 
        if x < 0 or x >= n or y < 0 or y >= m:
            return False
             
        return not grid[x][y]

使用dijstra解决：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
from typing import (
    List,
)
from lintcode import (
    Point,
)
import heapq
 
"""
Definition for a point:
class Point:
    def __init__(self, x=0, y=0):
        self.x = x
        self.y = y
"""
DIR = [(1, 2), (1, -2), (-1, 2), (-1, -2), (2, 1), (2, -1), (-2, 1), (-2, -1)]
 
 
class Solution:
    """
    @param grid: a chessboard included 0 (false) and 1 (true)
    @param source: a point
    @param destination: a point
    @return: the shortest path
    """
    def shortest_path(self, grid: List[List[bool]], source: Point, destination: Point) -> int:
        # write your code here
        r, c = len(grid), len(grid[0])
        root = (source.x, source.y)
        q = [(0, root, [root])]
        seen = {root}
        while q:
            cost, v, path = heapq.heappop(q)
            if v == (destination.x, destination.y):
                print(path)
                return cost
 
            x, y = v[0], v[1]
            for dx, dy in DIR:
                x2, y2 = x + dx, y + dy
                if 0 <= x2 < r and 0 <= y2 < c:
                    if grid[x2][y2] == 0 and (x2, y2) not in seen:               
                        heapq.heappush(q, (cost+1, (x2, y2), path+[(x2, y2)]))
                        seen.add((x2, y2))
 
        return -1

 

djkstra最短路问题，其实就是bfs不分层的模板，无非就是将deque修改为heapq而已，heapq中记录了路径距离优先级（下面程序如果不要path则去掉即可）：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import heapq
 
 
def shortest_path(graph, start, end):
    queue,seen = [(0, start, [])], {start}
    while queue:
        cost, v, path = heapq.heappop(queue)
        path = path + [v]
        if v == end:
            return cost, path
        for (neighbor_node, c) in graph[v].items():
            if neighbor_node not in seen:
                seen.add(neighbor_node)
                heapq.heappush(queue, (cost + c, neighbor_node, path))
    return -1, []
 
graph = {
'a': {'w': 14, 'x': 7, 'y': 9},
'b': {'w': 9, 'z': 6},
'w': {'a': 14, 'b': 9, 'y': 2},
'x': {'a': 7, 'y': 10, 'z': 10},
'y': {'a': 9, 'w': 2, 'x': 10, 'z': 11},
'z': {'b': 6, 'x': 15, 'y': 11},
}
cost, path = shortest_path(graph, start='a', end='z')
print(cost, path) 

==>比起上面的版本，我更喜欢下面的，在heappush的时候就存好所有遍历路径：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def shortest_path(graph, start, end):
    queue,seen = [(0, start, [start])], {start}
    while queue:
        cost, v, path = heapq.heappop(queue)       
        if v == end:
            return cost, path
             
        for (neighbor_node, c) in graph[v].items():
            if neighbor_node not in seen:
                seen.add(neighbor_node)
                heapq.heappush(queue, (cost + c, neighbor_node, path+[neighbor_node]))
    return -1, []
 
graph = {
'a': {'w': 14, 'x': 7, 'y': 9},
'b': {'w': 9, 'z': 6},
'w': {'a': 14, 'b': 9, 'y': 2},
'x': {'a': 7, 'y': 10, 'z': 10},
'y': {'a': 9, 'w': 2, 'x': 10, 'z': 11},
'z': {'b': 6, 'x': 15, 'y': 11},
}
cost, path = shortest_path(graph, start='a', end='z')
print(cost, path) 

 

包括单词ladder length的题目，使用dijstra也是比较高效的！

　　

拓扑排序定义

在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序（英语：Topological sorting）。

  • 每个顶点出现且只出现一次；
  • 若A在序列中排在B的前面，则在图中不存在从B到A的路径。

也可以定义为：拓扑排序是对有向无环图的顶点的一种排序，它使得如果存在一条从顶点A到顶点B的路径，那么在排序中B出现在A的后面。

(来自 Wiki)

实际运用

拓扑排序 Topological Sorting 是一个经典的图论问题。他实际的运用中，拓扑排序可以做如下的一些事情：

  • 检测编译时的循环依赖
  • 制定有依赖关系的任务的执行顺序
  • 实际应用就是大学生选课，应该按照哪种顺序进行选课，才能够顺利学完这些课程！
  • ==》例如，假定一个计算机专业的学生必须完成图3-4所列出的全部课程。在这里，课程代表活动，学习一门课程就表示进行一项活动，学习每门课程的先决条件是学完它的全部先修课程。如学习《数据结构》课程就必须安排在学完它的两门先修课程《离散数学》和《算法语言》之后。学习《高等数学》课程则可以随时安排，因为它是基础课程，没有先修课。 图中的每个顶点代表一门课程，每条有向边代表起点对应的课程是终点对应课程的先修课。从图中可以清楚地看出各课程之间的先修和后续的关系。如课程C5的先修课为C2，后续课程为C4和C6。 [2]

  •  

     

     

     ==》一种可行的选课方式：C1，C2，C5，C8，C9，C3，C4，C6，C7，就是一种拓扑排序！

拓扑排序不是一种排序算法

虽然名字里有 Sorting，但是相比起我们熟知的 Bubble Sort, Quick Sort 等算法，Topological Sorting 并不是一种严格意义上的 Sorting Algorithm。

确切的说，一张图的拓扑序列可以有很多个，也可能没有。拓扑排序只需要找到其中一个序列，无需找到所有序列。

 

入度与出度

在介绍算法之前，我们先介绍图论中的一个基本概念，入度和出度，英文为 in-degree & out-degree。
在有向图中，如果存在一条有向边 A-->B，那么我们认为这条边为 A 增加了一个出度，为 B 增加了一个入度。

算法流程

拓扑排序的算法是典型的宽度优先搜索算法，其大致流程如下：

  1. 统计所有点的入度，并初始化拓扑序列为空。
  2. 将所有入度为 0 的点，也就是那些没有任何依赖的点，放到宽度优先搜索的队列中
  3. 将队列中的点一个一个的释放出来，放到拓扑序列中，每次释放出某个点 A 的时候，就访问 A 的相邻点（所有A指向的点），并把这些点的入度减去 1。
  4. 如果发现某个点的入度被减去 1 之后变成了 0，则放入队列中。
  5. 直到队列为空时，算法结束，

深度优先搜索的拓扑排序

深度优先搜索也可以做拓扑排序，不过因为不容易理解，也并不推荐作为拓扑排序的主流算法。

 

127. 拓扑排序

中文English

给定一个有向图，图节点的拓扑排序定义如下:

  • 对于图中的每一条有向边 A -> B , 在拓扑排序中A一定在B之前.
  • 拓扑排序中的第一个节点可以是图中的任何一个没有其他节点指向它的节点.

针对给定的有向图找到任意一种拓扑排序的顺序.

Example

 

Challenge

能否分别用BFS和DFS完成？

Clarification

有关图的表示详情请看这里

Notice

你可以假设图中至少存在一种拓扑排序

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
"""
Definition for a Directed graph node
class DirectedGraphNode:
    def __init__(self, x):
        self.label = x
        self.neighbors = []
"""
 
class Solution:
    """
    @param graph: A list of Directed graph node
    @return: Any topological order for the given graph.
    """
    def topSort(self, graph):
        node_to_indegree = self.get_indegree(graph)
 
        # bfs
        order = []
        start_nodes = [n for n in graph if node_to_indegree[n] == 0]
        queue = collections.deque(start_nodes)
        while queue:
            node = queue.popleft()
            order.append(node)
            for neighbor in node.neighbors:
                node_to_indegree[neighbor] -= 1
                if node_to_indegree[neighbor] == 0:
                    queue.append(neighbor)
                 
        return order
     
    def get_indegree(self, graph):
        node_to_indegree = {x: 0 for x in graph}
 
        for node in graph:
            for neighbor in node.neighbors:
                node_to_indegree[neighbor] += 1
                 
        return node_to_indegree

 

615. 课程表

中文
English

现在你总共有 n 门课需要选，记为 0 到 n - 1.
一些课程在修之前需要先修另外的一些课程，比如要学习课程 0 你需要先学习课程 1 ，表示为[0,1]
给定n门课以及他们的先决条件，判断是否可能完成所有课程？

样例

例1:

输入: n = 2, prerequisites = [[1,0]] 
输出: true

例2:

输入: n = 2, prerequisites = [[1,0],[0,1]] 
输出: false
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from collections import deque
 
 
class Solution:
    # @param {int} numCourses a total of n courses
    # @param {int[][]} prerequisites a list of prerequisite pairs
    # @return {boolean} true if can finish all courses or false
    def canFinish(self, numCourses, prerequisites):
        # Write your code here
        edges = {i: [] for i in range(numCourses)}
        degrees = [0 for i in range(numCourses)]
        for i, j in prerequisites:
            edges[j].append(i)
            degrees[i] += 1
             
        queue, count = deque([]), 0
         
        for i in range(numCourses):
            if degrees[i] == 0:
                queue.append(i)
 
        while queue:
            node = queue.popleft()
            count += 1
 
            for x in edges[node]:
                degrees[x] -= 1
                if degrees[x] == 0:
                    queue.append(x)
 
        return count == numCourses

 

上面的写法比较简洁，另外我写的（20220605）：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from typing import (
    List,
)
 
class Solution:
    """
    @param num_courses: a total of n courses
    @param prerequisites: a list of prerequisite pairs
    @return: true if can finish all courses or false
    """
    def can_finish(self, num_courses: int, prerequisites: List[List[int]]) -> bool:
        # write your code here
        graph = self.build_graph(prerequisites, num_courses)
        degree = self.calc_indegree(num_courses, graph)
        q = collections.deque(self.get_head_nodes(degree))
        orders = self.top_sort(q, degree, graph)
        return len(orders) == num_courses
 
    def top_sort(self, q, degree, graph):
        ans = []
        while q:
            node = q.popleft()
            ans.append(node)
            for neibor in graph[node]:
                degree[neibor] -= 1
                if degree[neibor] == 0:
                    q.append(neibor)
         
        return ans
 
    def get_head_nodes(self, degree):
        return [node for node in degree if degree[node] == 0]
 
    def build_graph(self, arr, n):
        ans = {i: set() for i in range(n)}
        for i, j in arr:
            ans[j].add(i)
 
        return ans
 
    def calc_indegree(self, n, graph):
        indegree = {x: 0 for x in range(n)}
   
        for node in graph:
            for neighbor in graph[node]:
                indegree[neighbor] += 1
                   
        return indegree

 

　　

Dijkstra’s Algorithm 

单源最短路径Dijkstra算法：只能处理正权边，****可以有环****

Given a weighted graph and a starting (source) vertex in the graph, Dijkstra’s algorithm is used to find the shortest distance from the source node to all the other nodes in the graph.

As a result of the running Dijkstra’s algorithm on a graph, we obtain the shortest path tree (SPT) with the source vertex as root.

In Dijkstra’s algorithm, we maintain two sets or lists. One contains the vertices that are a part of the shortest-path tree (SPT) and the other contains vertices that are being evaluated to be included in SPT. Hence for every iteration, we find a vertex from the second list that has the shortest path.

The pseudocode for the Dijkstra’s shortest path algorithm is given below.

Pseudocode

Given below is the pseudocode for this algorithm. ===>下面这个伪代码就非常能够说明思路！！！如何去寻找最短的路径，使用的是previous一个hash表记录！

procedure dijkstra(G, S)
     G-> graph; S->starting vertex
begin
    for each vertex V in G          //initialization; initial path set to infinite
        path[V] <- infinite
        previous[V] <- NULL
        If V != S, add V to Priority Queue PQueue
    path [S] <- 0
     
    while PQueue IS NOT EMPTY
        U <- Extract MIN from PQueue
        for each unvisited adjacent_node  V of U
            tempDistance <- path [U] + edge_weight(U, V)
            if tempDistance < path [V]
                path [V] <- tempDistance
                previous[V] <- U
    return path[], previous[]
end

Let’s now take a sample graph and illustrate the Dijkstra’s shortest path algorithm.

shortest path algorithm

Initially, the SPT (Shortest Path Tree) set is set to infinity.

Let’s start with vertex 0. So to begin with we put the vertex 0 in sptSet.

sptSet = {0, INF, INF, INF, INF, INF}.

Next with vertex 0 in sptSet, we will explore its neighbors. Vertices 1 and 2 are two adjacent nodes of 0 with distance 2 and 1 respectively.

adjacent nodes

In the above figure, we have also updated each adjacent vertex (1 and 2) with their respective distance from source vertex 0. Now we see that vertex 2 has a minimum distance. So next we add vertex 2 to the sptSet. Also, we explore the neighbors of vertex 2.

adjacent vertex

Now we look for the vertex with minimum distance and those that are not there in spt. We pick vertex 1 with distance 2.

vertex with minimum distance

As we see in the above figure, out of all the adjacent nodes of 2, 0, and 1 are already in sptSet so we ignore them. Out of the adjacent nodes 5 and 3, 5 have the least cost. So we add it to the sptSet and explore its adjacent nodes.

adjacent nodes of 2, 0

In the above figure, we see that except for nodes 3 and 4, all the other nodes are in sptSet. Out of 3 and 4, node 3 has the least cost. So we put it in sptSet.

nodes 3 and 4

As shown above, now we have only one vertex left i.e. 4 and its distance from the root node is 16. Finally, we put it in sptSet to get the final sptSet = {0, 2, 1, 5, 3, 4} that gives us the distance of each vertex from the source node 0.

 

代码实现：

参考：https://www.softwaretestinghelp.com/dijkstras-algorithm-in-java/

https://gist.github.com/kachayev/5990802

如下，对原有代码进行了重构，增加可读性：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
from collections import defaultdict
from heapq import heappush, heappop
 
 
def dijkstra2(edges, start_node, end_node):
    graph = defaultdict(dict)
    for src, dst, distance in edges:
        graph[src][dst] = distance
 
    q = [(0, start_node, None)]
    found_min_dist_nodes = set()
    distances = {start_node: 0}
    back_paths = {}
 
    while q:
        cost, min_dist_node, src_node = heappop(q)
         
        # redundant, because we never push a vertex (we've already seen) to the heap
        # if min_dist_node in found_min_dist_nodes:
        #     continue
 
        found_min_dist_nodes.add(min_dist_node)
        back_paths[min_dist_node] = src_node
 
        if min_dist_node == end_node:
            return cost, back_paths
 
        for neibor_node, distance in graph[min_dist_node].items():
            if neibor_node in found_min_dist_nodes:
                continue
 
            prev_dist = distances.get(neibor_node, float('inf'))
            new_dist = cost + distance
            if new_dist < prev_dist:
                distances[neibor_node] = new_dist
                heappush(q, (new_dist, neibor_node, min_dist_node))
 
    return float("inf"), back_paths
 
 
def find_path(back_paths, start_node, end_node):
    ans = [end_node]
    while end_node != start_node:
        end_node = back_paths[end_node]
        ans.append(end_node)
 
    return ans[::-1]
 
 
def dijkstra(edges, f, t):
    g = defaultdict(list)
    for l,r,c in edges:
        g[l].append((c,r))
 
    q, seen, mins = [(0,f,())], set(), {f: 0}
    while q:
        (cost,v1,path) = heappop(q)
        if v1 not in seen:
            seen.add(v1)
            path = (v1, path)
            if v1 == t: return (cost, path)
 
            for c, v2 in g.get(v1, ()):
                if v2 in seen: continue
                prev = mins.get(v2, None)
                next = cost + c
                if prev is None or next < prev:
                    mins[v2] = next
                    heappush(q, (next, v2, path))
 
    return float("inf"), None
 
if __name__ == "__main__":
    edges = [
        ("A", "B", 7),
        ("A", "D", 5),
        ("B", "C", 8),
        ("B", "D", 9),
        ("B", "E", 7),
        ("C", "E", 5),
        ("D", "E", 15),
        ("D", "F", 6),
        ("E", "F", 8),
        ("E", "G", 9),
        ("F", "G", 11)
    ]
 
    edges2 = [(0, 1, 2),
              (0, 2, 1),
              (1, 0, 2),
              (1, 2, 7),
              (1, 4, 8),
              (1, 5, 4),
              (2, 0, 1),
              (2, 1, 7),
              (2, 5, 3),
              (2, 3, 7),
              (3, 2, 7),
              (3, 4, 8),
              (3, 5, 4),
              (4, 1, 8),
              (4, 3, 8),
              (4, 1, 8),
              (4, 5, 5),
              (5, 1, 4),
              (5, 2, 3),
              (5, 3, 4),
              (5, 4, 5)]
 
    print("=== Dijkstra ===")
    print(edges)
    print("A -> E:")
    print(dijkstra(edges, "A", "E"))
    print("F -> G:")
    print(dijkstra(edges, "F", "G"))
    print("0 -> 4:")
    print(dijkstra(edges2, 0, 4))
 
    print("A -> E:")
    dist, backpaths = dijkstra2(edges, "A", "E")
    print(dist, backpaths)
    print(find_path(backpaths, "A", "E"))
    print("F -> G:")
    print(dijkstra2(edges, "F", "G"))
    print("0 -> 4:")
    dist, backpaths = (dijkstra2(edges2, 0, 4))
    print(dist, backpaths)
    print(find_path(backpaths, 0, 4))

　　

算法模板的话，就记这个：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
rom collections import defaultdict
from heapq import heappush, heappop
 
 
def dijkstra2(edges, start_node, end_node):
    graph = defaultdict(dict)
    for src, dst, distance in edges:
        graph[src][dst] = distance
 
    q = [(0, start_node, None)]
    found_min_dist_nodes = set()
    distances = {start_node: 0}
    back_paths = {}
 
    while q:
        cost, min_dist_node, src_node = heappop(q)
 
        # redundant, because we never push a vertex (we've already seen) to the heap
        # if min_dist_node in found_min_dist_nodes:
        #     continue
 
        found_min_dist_nodes.add(min_dist_node)
        back_paths[min_dist_node] = src_node
 
        if min_dist_node == end_node:
            return cost, back_paths
 
        for neibor_node, distance in graph[min_dist_node].items():
            if neibor_node in found_min_dist_nodes:
                continue
 
            prev_dist = distances.get(neibor_node, float('inf'))
            new_dist = cost + distance
            if new_dist < prev_dist:
                distances[neibor_node] = new_dist
                heappush(q, (new_dist, neibor_node, min_dist_node))
 
    return float("inf"), back_paths
 
 
def find_path(back_paths, start_node, end_node):
    ans = [end_node]
    while end_node != start_node:
        end_node = back_paths[end_node]
        ans.append(end_node)
 
    return ans[::-1]

 

如果不要求具体路径（大多数题目都不会），只是计算距离的话，用下面的模板：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
from collections import defaultdict
from heapq import heappush, heappop
 
def dijkstra(edges, start_node, end_node):
    graph = build_graph(edges)
    return calc_min_distance(graph, start_node, end_node)
 
 
def build_graph(edges):
    graph = defaultdict(dict)
    for src, dst, distance in edges:
        graph[src][dst] = distance
        # graph[dst][src] = distance #无向图的话，要加这个
    return graph
 
 
def calc_min_distance(graph, start_node, end_node):
    q = [(0, start_node)]
    found_min_dist_nodes = set()
    distances = {start_node: 0}
 
    while q:
        cost, min_dist_node = heappop(q)
 
        found_min_dist_nodes.add(min_dist_node)
 
        if min_dist_node == end_node:
            return cost
 
        # 如果是矩阵，获得邻居节点的表达方式要修改
        for neibor_node, distance in graph[min_dist_node].items():
            if neibor_node in found_min_dist_nodes:
                continue
 
            prev_dist = distances.get(neibor_node, float('inf'))
            # 下面距离的计算通常要修改
            new_dist = cost + distance
            if new_dist < prev_dist:
                distances[neibor_node] = new_dist
                # 如果是求解最大值，通常要push一个负值，取出来后再取反
                heappush(q, (new_dist, neibor_node))
 
    return float("inf")
 
 
if __name__ == "__main__":
    edges = [
        ("A", "B", 7),
        ("A", "D", 5),
        ("B", "C", 8),
        ("B", "D", 9),
        ("B", "E", 7),
        ("C", "E", 5),
        ("D", "E", 15),
        ("D", "F", 6),
        ("E", "F", 8),
        ("E", "G", 9),
        ("F", "G", 11)
    ]
 
    print("=== Dijkstra ===")
    print("*"*66)
    print("A -> E:")
    dist = dijkstra(edges, "A", "E")
    print(dist)
    print("F -> G:")
    print(dijkstra(edges, "F", "G"))
    print("*"*66)

　　

　　

743. 网络延迟时间

见：https://leetcode.cn/problems/network-delay-time/ 

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

 

示例 1：

输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出：2

示例 2：

输入：times = [[1,2,1]], n = 2, k = 1
输出：1

示例 3：

输入：times = [[1,2,1]], n = 2, k = 2
输出：-1

 

这个题目，本质上就是dijstra，但是只有start_node，没有end_node，可以说是dijstra的阉割版本！代码如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
from collections import defaultdict
from heapq import heappush, heappop
 
 
class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        distances = self.dijkstra2(times, k)
        if len(distances) != n:
            return -1
         
        return max(distances.values())
 
    def dijkstra2(self, edges, start_node):
        graph = defaultdict(dict)
        for src, dst, distance in edges:
            graph[src][dst] = distance
 
        q = [(0, start_node, None)]
        found_min_dist_nodes = set()
        distances = {start_node: 0}
        back_paths = {}
 
        while q:
            cost, min_dist_node, src_node = heappop(q)
 
            # redundant, because we never push a vertex (we've already seen) to the heap
            # if min_dist_node in found_min_dist_nodes:
            #     continue
 
            found_min_dist_nodes.add(min_dist_node)
            back_paths[min_dist_node] = src_node
 
            # if min_dist_node == end_node:
            #     return cost, back_paths
 
            for neibor_node, distance in graph[min_dist_node].items():
                if neibor_node in found_min_dist_nodes:
                    continue
 
                prev_dist = distances.get(neibor_node, float('inf'))
                new_dist = cost + distance
                if new_dist < prev_dist:
                    distances[neibor_node] = new_dist
                    heappush(q, (new_dist, neibor_node, min_dist_node))
 
        return distances

　　

1631. 最小体力消耗路径

难度中等

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

 

示例 1：

输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
from collections import defaultdict
from heapq import heappush, heappop
 
 
DIR = [(-1, 0), (1, 0), (0, -1), (0, 1)]
 
class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        return self.dijkstra2(heights)
 
 
    def dijkstra2(self, heights):
        m, n = len(heights), len(heights[0])
        start_node = (0, 0)
        end_node = (m-1, n-1)
         
        q = [(0, start_node)]
        found_min_dist_nodes = set()
        distances = {start_node: 0}
 
        while q:
            cost, min_dist_node = heappop(q)
            found_min_dist_nodes.add(min_dist_node)
 
            if min_dist_node == end_node:
                return cost
 
            x, y = min_dist_node[0], min_dist_node[1]
            for i in range(4):
                nx = x + DIR[i][0]
                ny = y + DIR[i][1]
                if nx >= 0 and nx < m and ny >= 0 and ny < n:
                    new_dist = max(cost, abs(heights[x][y] - heights[nx][ny]))
                    prev_dist = distances.get((nx, ny), float('inf'))
                    if new_dist < prev_dist:
                        distances[(nx, ny)] = new_dist               
                        heappush(q, (new_dist, (nx, ny)))       
 
        return -1

　　



1514. 概率最大的路径

https://leetcode.cn/problems/path-with-maximum-probability/

难度中等

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

 

示例 1：

输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

示例 2：

输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出：0.30000

示例 3：

输入：n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出：0.00000
解释：节点 0 和 节点 2 之间不存在路径

 
 
?
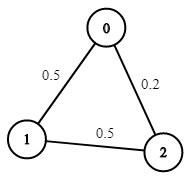
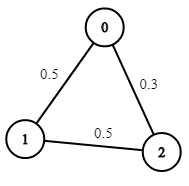
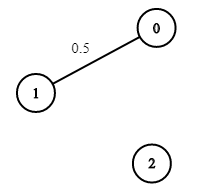
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from collections import defaultdict
from heapq import heappush, heappop
 
 
class Solution:
    def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:
        g = self.construct(edges, succProb)
        return self.dijkstra2(g, start, end)
 
    def construct(self, e, p):
        return [(e[i][0], e[i][1], p[i]) for i in range(0, len(p))]
 
    def dijkstra2(self, edges, start_node, end_node):
        graph = defaultdict(dict)
        for src, dst, distance in edges:
            graph[src][dst] = distance
            graph[dst][src] = distance
 
        q = [(-1, start_node)]
        found_min_dist_nodes = set()
        distances = {start_node: 0}
        back_paths = {}
 
        while q:
            val, min_dist_node = heappop(q)
            cost = -val
            # redundant, because we never push a vertex (we've already seen) to the heap
            # if min_dist_node in found_min_dist_nodes:
            #     continue
 
            found_min_dist_nodes.add(min_dist_node)
 
            if min_dist_node == end_node:
                return cost
 
            for neibor_node, distance in graph[min_dist_node].items():
                if neibor_node in found_min_dist_nodes:
                    continue
 
                prev_dist = distances.get(neibor_node, 0)
                new_dist = cost * distance
 
                if new_dist > prev_dist:
                    distances[neibor_node] = new_dist
                    heappush(q, (-new_dist, neibor_node))
 
        return 0

　　

posted @   bonelee  阅读(1061)  评论(1)  编辑  收藏  举报
编辑推荐：
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 理解Rust引用及其生命周期标识（上）
· 浏览器原生「磁吸」效果！Anchor Positioning 锚点定位神器解析
· 没有源码，如何修改代码逻辑？
阅读排行：
· 全程不用写代码，我用AI程序员写了一个飞机大战
· MongoDB 8.0这个新功能碉堡了，比商业数据库还牛
· 记一次.NET内存居高不下排查解决与启示
· 白话解读 Dapr 1.15：你的「微服务管家」又秀新绝活了
· DeepSeek 开源周回顾「GitHub 热点速览」
历史上的今天：
2017-10-23 递归神经网络——就是解决AST这样的问题
2017-10-23 循环神经网络
2017-10-23 卷积神经网络——本质上是在利用卷积做特征压缩，然后再全连接
2017-10-23 神经网络和反向传播算法——反向传播算法本质上是随机梯度下降，链式求导法则而来的
2017-10-23 LSTM入门学习——结合《LSTM模型》文章看
2017-10-23 LSTM入门学习——本质上就是比RNN的隐藏层公式稍微复杂了一点点而已
2017-10-23 LSTM模型
点击右上角即可分享
微信分享提示