螺旋矩阵打印

from：http://blog.51cto.com/acevi/2141009

题目如下

 

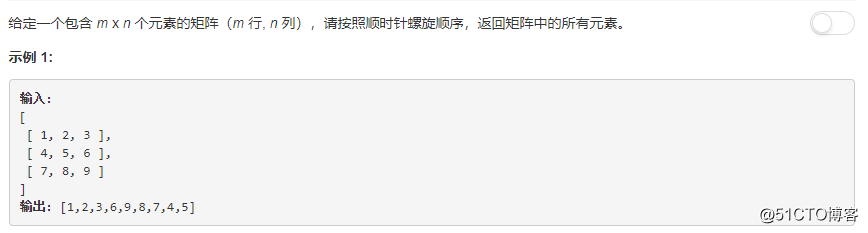
分析

       不难发现，按照顺时针螺旋顺序遍历矩阵其实就只有四个方向：顶层行从左往右；右边列从上到下；底层行从右往左；左边列从下往上。遍历完这四个方向之后就表示已经遍历完了一圈，下一圈也同样是这四个方向，只是初始位置和结束位置会在每一轮遍历之后发生变化。

       下面介绍两种方法，思想基本一致，不同之处是对边界的判断和位置的移动。

方法一

public class SpiralMatrix {
     public static List<Integer> spiralMatrixOlder(int[][] matrix) {
          List<Integer> res = new ArrayList<Integer>();
          if(matrix.length == 0)
              return res;
          
          int rowBegin = 0;
          int colBegin = 0;
          int rowEnd = matrix.length - 1; //行
          int colEnd = matrix[0].length - 1; //列
          
          /*
           * Time Complexity: O(N)
           * Space Complexity:O(N)*/
          while(rowBegin <= rowEnd && colBegin <= colEnd){
              
                   //底层行从左往右
                   for(int i = colBegin;i <= colEnd;i++) {
                        res.add(matrix[rowBegin][i]);
                   }
                   rowBegin++; //处理完一行后往下移一行
                   
                   //右边列从上往下
                   for(int i = rowBegin ;i <= rowEnd;i++) {
                        res.add(matrix[i][colEnd]);
                   }
                   colEnd--; //处理完一列往前移一列
                   
                   //底层行从右往左
                   if(rowBegin <= rowEnd) {
                        for(int j = colEnd;j>=colBegin;j--){
                             res.add(matrix[rowEnd][j]);
                        }
                        rowEnd--;
                   }
                   
                   //左边列从下往上
                   if(colBegin <= colEnd) {
                        for(int j = rowEnd;j >= rowBegin ; j--) {
                             res.add(matrix[j][colBegin]);
                        }
                        colBegin++;
                   }
                   
          }
          return res;
          
     }


类似的：

public class Solution 
{
    public int[][] generateMatrix(int n) 
    {
        int[][] res = new int[n][n];
        
        int total = n*n;
        int num = 1;
        
        int rowBegin = 0;
        int rowEnd = n-1;
        int colBegin = 0;
        int colEnd = n-1;
        
        while(num <= total)
        {
            // traverse right (y changes)
            for(int y=colBegin; y<=colEnd; y++)
                res[rowBegin][y] = num++;
            
            rowBegin++; // move down one row
            
            // traverse down (x changes)
            for(int x=rowBegin; x<=rowEnd; x++)
                res[x][colEnd] = num++;
            
            colEnd--; // move left one column
            
            // traverse left (y changes)
            for(int y=colEnd; y>=colBegin; y--)
                res[rowEnd][y] = num++;
            
            rowEnd--; // move up one row
            
            // traverse up (x changes)
            for(int x=rowEnd; x>=rowBegin; x--)
                res[x][colBegin] = num++;
            
            colBegin++; // move right one column
            
        }
        
        return res;
    }
}