两个有序数组的中位数（第k大的数）——使用二分答案的思路写起来更直观

问题：两个已经排好序的数组，找出两个数组合并后的中位数（如果两个数组的元素数目是偶数，返回上中位数）。

感觉这种题目挺难的，尤其是将算法完全写对。因为当初自己微软面试的时候遇到了，但是没有想出来思路。看网上写了一堆解法，但是将思路说得非常清楚的少之又少。

有两种思路，一个是算法导论里面的，一个是求解k大元素。建议使用下面第二种思路，也就是leetcode代码，代码少不容易出错。

see: https://www.lintcode.com/problem/median-of-two-sorted-arrays/description

65. 两个排序数组的中位数

说明

中位数的定义：

这里的中位数等同于数学定义里的中位数。
中位数是排序后数组的中间值。
如果有数组中有n个数且n是奇数，则中位数为
如果有数组中有n个数且n是偶数，则中位数为
比如：数组A=[1,2,3]的中位数是2，数组A=[1,19]的中位数是10。

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        def findKth(A, l_a, r_a, B, l_b, r_b, k):
            rangeA = r_a - l_a + 1
            rangeB = r_b - l_b + 1
 
            if rangeA == 0:
                return B[l_b+k-1]
 
            if rangeB == 0:
                return A[l_a+k-1]
 
            if k == 1: # 注意位置，是放在上面2个if后面，k为1时，只需要返回A B首个元素最小即可
                return min(A[l_a], B[l_b])
 
            if rangeA > rangeB: # 之所有要交换，是因为后面pb = k - pa可能导致l_b + pb越界！例如：A有100个元素，B只有1个，k为50的情形
                return findKth(B, l_b, r_b, A, l_a, r_a, k)
 
            pa = min(k // 2, rangeA)
            pb = k - pa
 
            if A[l_a + pa - 1] == B[l_b + pb - 1]:
                return A[l_a + pa - 1]
            elif A[l_a + pa - 1] < B[l_b + pb - 1]:
                return findKth(A, l_a + pa, r_a, B, l_b, l_b + pb - 1, k - pa) # 注意收缩r_b为l_b + pb - 1
            else:
                return findKth(A, l_a, l_a + pa - 1, B, l_b + pb, r_b, k - pb)
        
        A, B = nums1, nums2
        k = len(A) + len(B)
        if k & 1:
            return findKth(A, 0, len(A) - 1, B, 0, len(B) - 1, k//2 + 1) # 注意有+1，因为是第k大
        else:
            a = findKth(A, 0, len(A) - 1, B, 0, len(B) - 1, k//2 + 1) # 注意有+1，因为是第k大
            b = findKth(A, 0, len(A) - 1, B, 0, len(B) - 1, k//2)
            return (a + b)/2

下面的内容摘自：https://blog.csdn.net/hackbuteer1/article/details/7584838

求解中位数，算法导论上面的分析是这样的：
Say the two arrays are sorted and increasing, namely A and B.
It is easy to find the median of each array in O(1) time.
Assume the median of array A is m and the median of array B is n. Then，
1、If m==n，then clearly the median after merging is also m，the algorithm holds.
2、If m<=n，then reserve the half of sequence A in which all numbers are greater than m，also reserve the half of sequence B in which all numbers are smaller than n.
Run the algorithm on the two new arrays。
3、If m>n，then reserve the half of sequence A in which all numbers are smaller than m，also reserve the half of sequence B in which all numbers are larger than n.
Run the algorithm on the two new arrays。
Time complexity: O(logn)
下面，我们来画个图，分析一下这个思路：

我们先来分析看看：想到对数的效率，首先想到的就是二分查找，对于这个题目二分查找的意义在哪里呢？
我们找到了A[n/2] 和 B[n/2]来比较，
1、如果他们相等，那样的话，我们的搜索结束了，因为答案已经找到了A[n/2]就肯定是排序后的中位数了。
2、如果我们发现B[n/2] > A[n/2]，说明什么，这个数字应该在 A[n/2]->A[n]这个序列里面，或者在 B[1]-B[n/2]这里面。或者，这里的或者是很重要的，我们可以说，我们已经成功的把问题变成了在排序完成的数组A[n/2]-A[n]和B[0]-B[n/2]里面找到合并以后的中位数，显然递归是个不错的选择了。
3、如果B[n/2] < A[n/2]呢？显然就是在A[0]-A[n/2]和B[n/2]-B[n]里面寻找了。
在继续想，这个递归什么时候收敛呢？当然一个case就是相等的值出现，如果不出现等到这个n==1的时候也就结束了。
照着这样的思路，我们比较容易写出如下的代码，当然边界的值需要自己思量一下（递归代码如下）：
// 两个长度相等的有序数组寻找中位数
int Find_Media_Equal_Length(int a[] , int b[] , int length)
{
 if(length == 1)
 {
 return a[0] > b[0] ? b[0] : a[0];
 }
 int mid = (length-1)/2; //奇数就取中间的，偶数则去坐标小的
 if(a[mid] == b[mid])
 return a[mid];
 else if(a[mid] < b[mid])
 {
 return Find_Media_Equal_Length(&a[length-mid-1] , &b[0] , mid+1); //偶数则取剩下的length/2，奇数则取剩下的length/2+1
 //return Find_Media_Equal_Length(a+length-mid-1 , b , mid+1);
 }
 else
 {
 return Find_Media_Equal_Length(&a[0] , &b[length-mid-1] , mid+1);
 //return Find_Media_Equal_Length(a , b+length-mid-1 , mid+1);
 }
}

二：马上有人说那不定长的怎么办呢？一样的，我们还是来画个图看看：

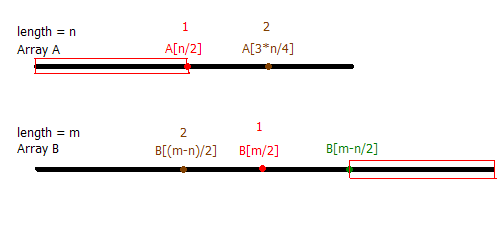
因为一个常识：如果我们去掉数组比中位数小的k个数，再去掉比中位数大的k个数，得到的子数组的中位数和原来的中位数相同。

一样的，我们还是把这个两个数组来比较一下，不失一般性，我们假定B数组比A数组长一点。A的长度为n, B的长度为m。比较A[n/2]和B[m/2] 时候。类似的，我们还是分成几种情况来讨论：
a、如果A[n/2] == B[m/2]，那么很显然，我们的讨论结束了。A[n/2]就已经是中位数，这个和他们各自的长度是奇数或者偶数无关。
b、如果A[n/2] < B[m/2]，那么，我们可以知道这个中位数肯定不在[A[0]---A[n/2])这个区间内，同时也不在[B[m/2]---B[m]]这个区间里面。这个时候，我们不能冲动地把[A[0]---A[n/2])和[B[m/2]---B[m]]全部扔掉。我们只需要把[B[m-n/2]---B[m]]和[A[0]---A[n/2])扔掉就可以了。（如图所示的红色线框），这样我们就把我们的问题成功转换成了如何在A[n/2]->A[n]这个长度为 n/2 的数组和 B[1]-B[m-n/2]这个长度为m-n/2的数组里面找中位数了，问题复杂度即可下降了。
c、只剩下A[n/2] > B[m/2]，和b类似的，我们可以把A[n/2]->A[n]这块以及B[1]->B[n/2]这块扔掉了就行，然后继续递归。
我们也可以写出如下的代码：
// 两个长度不相等的有序数组寻找中位数
int Find_Media_Random_Length(int a[] , int lengtha , int b[] , int lengthb)
{
 int mida = lengtha/2;
 int midb = lengthb/2;
 int l = (mida <= midb) ? mida : midb;
 if(lengtha == 1)
 {
 if(lengthb % 2 == 0)
 {
 if(a[0] >= b[midb])
 return b[midb];
 else if(a[0] <= b[midb-1])
 return b[midb-1];
 return a[0];
 }
 else
 return b[midb];
 }
 else if(lengthb == 1)
 {
 if(lengtha % 2 == 0)
 {
 if(b[0] >= a[mida])
 return a[mida];
 else if(b[0] <= a[mida-1])
 return a[mida-1];
 return b[0];
 }
 else
 return a[mida];
 }
 if(a[mida] == b[midb])
 return a[mida];
 else if(a[mida] < b[midb])
 return Find_Media_Random_Length(&a[mida] , lengtha-l , &b[0] , lengthb-l);
 else
 return Find_Media_Random_Length(&a[0] , lengtha-l , &b[midb] , lengthb-l);
}
代码果然很蛋疼。。。。

摘自：https://blog.csdn.net/yutianzuijin/article/details/11499917

根据算法导论中的方法，但是该方法会存在无穷多的边界细节问题，而且扩展也不见得正确，这个可从各网页的评论看出，非常不建议大家走这条路。

最后从medianof two sorted arrays中看到了一种非常好的方法。原文用英文进行解释，在此我们将其翻译成汉语。该方法的核心是将原问题转变成一个寻找第k小数的问题（假设两个原序列升序排列），这样中位数实际上是第(m+n)/2小的数。所以只要解决了第k小数的问题，原问题也得以解决。

首先假设数组A和B的元素个数都大于k/2，我们比较A[k/2-1]和B[k/2-1]两个元素，这两个元素分别表示A的第k/2小的元素和B的第k/2小的元素。这两个元素比较共有三种情况：>、<和=。如果A[k/2-1]<B[k/2-1]，这表示A[0]到A[k/2-1]的元素都在A和B合并之后的前k小的元素中。换句话说，A[k/2-1]不可能大于两数组合并之后的第k小值，所以我们可以将其抛弃。

证明也很简单，可以采用反证法。假设A[k/2-1]大于合并之后的第k小值，我们不妨假定其为第（k+1）小值。由于A[k/2-1]小于B[k/2-1]，所以B[k/2-1]至少是第（k+2）小值。但实际上，在A中至多存在k/2-1个元素小于A[k/2-1]，B中也至多存在k/2-1个元素小于A[k/2-1]，所以小于A[k/2-1]的元素个数至多有k/2+ k/2-2，小于k，这与A[k/2-1]是第（k+1）的数矛盾。

当A[k/2-1]>B[k/2-1]时存在类似的结论。

当A[k/2-1]=B[k/2-1]时，我们已经找到了第k小的数，也即这个相等的元素，我们将其记为m。由于在A和B中分别有k/2-1个元素小于m，所以m即是第k小的数。(这里可能有人会有疑问，如果k为奇数，则m不是中位数。这里是进行了理想化考虑，在实际代码中略有不同，是先求k/2，然后利用k-k/2获得另一个数。)

通过上面的分析，我们即可以采用递归的方式实现寻找第k小的数。此外我们还需要考虑几个边界条件：

如果A或者B为空，则直接返回B[k-1]或者A[k-1]；
如果k为1，我们只需要返回A[0]和B[0]中的较小值；
如果A[k/2-1]=B[k/2-1]，返回其中一个；
最终实现的代码为：

double findKth(int a[], int m, int b[], int n, int k)
{
 //always assume that m is equal or smaller than n
 if (m > n)
 return findKth(b, n, a, m, k);
 if (m == 0)
 return b[k - 1];
 if (k == 1)
 return min(a[0], b[0]);
 //divide k into two parts
 int pa = min(k / 2, m), pb = k - pa;
 if (a[pa - 1] < b[pb - 1])
 return findKth(a + pa, m - pa, b, n, k - pa);
 else if (a[pa - 1] > b[pb - 1])
 return findKth(a, m, b + pb, n - pb, k - pb);
 else
 return a[pa - 1];
}

class Solution
{
public:
 double findMedianSortedArrays(int A[], int m, int B[], int n)
 {
 int total = m + n;
 if (total & 0x1)
 return findKth(A, m, B, n, total / 2 + 1);
 else
 return (findKth(A, m, B, n, total / 2)
 + findKth(A, m, B, n, total / 2 + 1)) / 2;
 }
};
我们可以看出，代码非常简洁，而且效率也很高。在最好情况下，每次都有k一半的元素被删除，所以算法复杂度为logk，由于求中位数时k为（m+n）/2，所以算法复杂度为log(m+n)。

详细代码见最前面！！！

如果上面的思路没有看懂的话，https://www.cnblogs.com/voidsky/p/5373982.html 这里面使用切割的思路特别容易明白！

问题介绍

这是个超级超级经典的分治算法！！这个问题大致是说，如何在给定的两个有序数组里面找其中的中值，或者变形问题，如何在2个有序数组数组中查找Top K的值（Top K的问题可以转换成求第k个元素的问题）。这个算法在很多实际应用中都会用到，特别是在当前大数据的背景下。

我觉得下面的这个思路特别好，特别容易理解！！请按顺序看。是来自leetcode上的stellari英文答案，我整理并自己修改了一下。

预备知识

先解释下“割”

我们通过切一刀，能够把有序数组分成左右两个部分，切的那一刀就被称为割(Cut)，割的左右会有两个元素，分别是左边最大值和右边最小值。
我们定义L = Max(LeftPart)，R = Min(RightPart)

Ps. 割可以割在两个数中间，也可以割在1个数上，如果割在一个数上，那么这个数即属于左边，也属于右边。（后面讲单数组中值问题的时候会说）

比如说[2 3 5 7]这个序列，割就在3和5之间
[2 3 / 5 7]
中值就是（3+5）/2 = 4

如果[2 3 4 5 6]这个序列，割在4上，我们可以把4分成2个
[2 3 (4/4) 5 7]
中值就是（4+4）/2 = 4

这样可以保证不管中值是1个数还是2个数都能统一运算。

割和第k个元素

对于单数组，找其中的第k个元素特别好做，我们用割的思想就是：

常识1：如果在k的位置割一下，然后A[k]就是L。换言之，就是如果左侧有k个元素，A[k]属于左边部分的最大值。（都是明显的事情，这个不用解释吧！）

双数组

我们设:
<msub><mi>C</mi><mi>i</mi></msub></math>">Ci为第i个数组的割。
<msub><mi>L</mi><mi>i</mi></msub></math>">Li为第i个数组割后的左元素.
<msub><mi>R</mi><mi>i</mi></msub></math>">Ri为第i个数组割后的右元素。

图片特么粘贴不上！！！

如何从双数组里取出第k个元素

这里写图片描述

首先<msub><mi>L</mi><mi>i</mi></msub><mo>&lt;=</mo><msub><mi>R</mi><mi>i</mi></msub></math>">Li<=Ri
如果我们让<msub><mi>L</mi><mn>1</mn></msub><mo>&lt;=</mo><msub><mi>R</mi><mn>2</mn></msub></math>">L1<=R2
那么左半边全小于右半边，如果左边的元素个数相加刚好等于k，那么第k个元素就是Max(L1,L2)，参考上面常识1。
如果 L1>R2，说明数组1的左边元素太大（多），我们把C1减小，把C2增大。L2>R1同理，把C1增大，C2减小。

假设k=3

对于
<mo stretchy="false">[</mo><mn>1</mn><mtext>&#xA0;</mtext><mn>4</mn><mtext>&#xA0;</mtext><mn>7</mn><mtext>&#xA0;</mtext><mn>9</mn><mo stretchy="false">]</mo></math>">[1 4 7 9]

设C1 = 2，那么C2 = k-C1 = 1
<mo stretchy="false">[</mo><mn>1</mn><mtext>&#xA0;</mtext><mn>4</mn><mrow class="MJX-TeXAtom-ORD"><mo>/</mo></mrow><mn>7</mn><mtext>&#xA0;</mtext><mn>9</mn><mo stretchy="false">]</mo></math>">[1 4/7 9]

这时候，L1(4)>R2(3)，说明C1要减小，C2要增大，C1 = 1，C2=k-C1 = 2
<mo stretchy="false">[</mo><mn>1</mn><mrow class="MJX-TeXAtom-ORD"><mo>/</mo></mrow><mn>4</mn><mtext>&#xA0;</mtext><mn>7</mn><mtext>&#xA0;</mtext><mn>9</mn><mo stretchy="false">]</mo></math>">[1/4 7 9]

这时候，满足了<msub><mi>L</mi><mn>1</mn></msub><mo>&lt;=</mo><msub><mi>R</mi><mn>2</mn></msub></math>">L1<=R2

如果对于上面的例子，把k改成4就恰好是中值。

posted @ 2019-01-03 23:14 bonelee 阅读(17504) 评论(1) 编辑收藏举报

刷新页面返回顶部

将者，智、信、仁、勇、严也。

Hi，我是李智华，华为-安全AI算法专家，欢迎来到安全攻防对抗的有趣世界。

两个有序数组的中位数（第k大的数）——使用二分答案的思路写起来更直观

65. 两个排序数组的中位数

问题介绍

预备知识

先解释下“割”

割和第k个元素

双数组

如何从双数组里取出第k个元素

假设k=3

公告

将者，智、信、仁、勇、严也。

Hi，我是李智华，华为-安全AI算法专家，欢迎来到安全攻防对抗的有趣世界。

两个有序数组的中位数（第k大的数）——使用二分答案的思路写起来更直观

65. 两个排序数组的中位数

样例

挑战

说明

问题介绍

预备知识

先解释下“割”

割和第k个元素

双数组

如何从双数组里取出第k个元素

假设k=3

公告