2 ,8 ,10,16进制快速转换的技巧

目录

• 前言提示
• • 0-8的二进制次方数
• 学习内容
• • 2进制转10进制
  • 2进制转8进制
  • 2进制转16进制
  • 8进制转2进制
  • 8进制转10进制
  • 8进制转16进制
  • 10进制转2进制
  • 10进制转8进制
  • 10进制转16进制
  • 16进制转2进制
  • 16进制转8进制
  • 16进制转10进制

前言提示

以下知识必背,良好基础和技巧,才能让你更快的学习和熟练

• 2 进制表示符号: B ，8 进制表示符号: O ，10 进制表示符号: D ，16 进制表示符号: H .

• 16进制 1-9 后 是 A - F , 并不是 10 -16 .

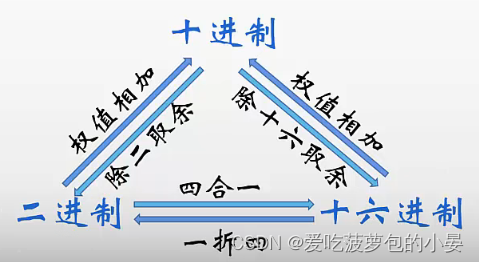
• 2 ,8 ,16 进制转换为10进制都是权值相加

• 10 进制转换为 2 , 8, 16 进制都是除对应进制数取余

• 8 和 16 进制的转换需要先转换为其他进制，再转换为目标进制

• 将 0-8 的二进制次方数记住能极大提升转换 2 进制数的速度 .

• 整数部分最前面的 0 可以去除, 小数最后面的 0 可以去除
  

---

0-8的二进制次方数

$2^0$=1	$2^1$=2	$2^2$=4	$2^3$=8
$2^4$=16	$2^5$=32	$2^6$=64	$2^6$=128

---

学习内容

2进制转10进制

10100111 B = $\underline{167}$ D

从字母B往左数，权重从0开始，所以D左边的 1 表示 1 * $2^0$ = 1 , 再往左权重加 1 ,所以第二个1 为 1 * $2^1$ = 2 , 为零不计算 .

把$全部计算的数字再相加$,就是10进制的得数.
128 + 32 + 4 + 2 + 1 = 167 D

---

2进制转8进制

10100111 B = $\underline{247}$ O

先将2进制数，从右往左，3个为一组进行分组,不够3个前面补0
分组后 : 010 100 111

分别计算$各小组内转换为10进制的得数$
010 B = 2 ， 100 B = 4 ， 111 B = 7

将数字从左往右排列后就是8进制的得数 ： 247 D

---

2进制转16进制

10100111 B = $\underline{247}$ O

先将2进制数，从右往左，4个为一组进行分组,不够4个前面补0
分组后 : 1010 0111

分别计算$各小组内转换为10进制的得数$
1010 B = 10 ，0111 B = 7

将数字从左往右排列后就是16进制的得数 ： A7 H

提示: 16 进制 1-9 后 就是 A - F

---

8进制转2进制

56 O = $\underline{247}$ B

先将每个数字分开
分开后 : 5 6

分别计算$单个数字的二进制得数$
5 O = 101 B，6 O = 110 B

将得数从左往右排列后就是2进制的得数 ： 101110 B

---

8进制转10进制

56 O = $\underline{46}$ D

从字母D往左数，权重从0开始，所以B左边的 1 表示 6 * $8^0$ = 6 , 再往左权重加 1 ,所以第二个1 为 5 * $8^1$ = 40 , 为零不计算 .

把$全部计算的数字再相加$,就是10进制的得数.
40 + 6 = 46 D

---

8进制转16进制

56 O = $\underline{2E}$ H

方法1: 先将八进制转换成二进制，再将二进制转换成十六进制
方法2: 先将八进制转换成十进制，再将十进制转换成十六进制

我们使用方法2,。
56 O = 46 D

此时应该回忆起开头的技巧, 10 进制转换其他进制都是除对应进制数取余

将10进制数不断的除以16 , 直到商为0 , 最后把余数逆向取得.
46 / 16 = 2 …14
2 / 16 = 0 …2

逆向取得余数: 2E H

$方法1可看16进制转换8进制$

---

10进制转2进制

202 D = $\underline{11001010}$ B

将10进制数不断的除以2 , 直到商为0 , 最后把余数逆向取得.
202 / 2 = 101 …0
101 / 2 = 50 …1
50 / 2 = 25 …0
25 / 2 = 12 …1
12/ 2 = 6 …0
6 / 2 = 3 …0
3 / 2 = 1 …1
1 / 2 = 0 …1

逆向取得余数: 11001010 B

---

10进制转8进制

202 D = $\underline{312}$ O

将10进制数不断的除以8 , 直到商为0 , 最后把余数逆向取得.
202 / 8 = 25 …2
25 / 8 = 3 …1
3 / 8 = 0 … 3

逆向取得余数: 312 O

---

10进制转16进制

202 D = $\underline{CA}$ H

将10进制数不断的除以16 , 直到商为0 , 最后把余数逆向取得.
202 / 16 = 12 …10
12 / 16 = 0 …12

逆向取得余数: CA H

---

16进制转2进制

202 H = $\underline{1000000010}$ B

先将每个数字分开
分开后 : 2 0 2

分别计算$单个数字的二进制得数$
2 H = 0010 B，0 H = 0000 B , 2 H = 0010 B

将得数从左往右排列后就是2进制的得数 ： 1000000010 B

---

16进制转8进制

202 H = $\underline{1000000010}$ O

第一种：他们之间的转换可以先转成二进制然后再相互转换。
第二种：他们之间的转换可以先转成十进制然后再相互转换。

我们使用方法1.
202 H = $\underline{1000000010}$ B
1000000010 B = 1002 O

$方法2可看8进制转换16进制$

---

16进制转10进制

202 H = $\underline{514}$ D

从字母D往左数，权重从0开始，所以D左边的 1 表示 2 * $16^0$ = 6 , 再往左权重加 1 ,所以第3个2 为 2 * $16^2$ = 512 , 为零不计算 .

把$全部计算的数字再相加$,就是10进制的得数.
512 + 0 + 2 = 514 D

---