LeetCode买卖股票之一：基本套路(122)

欢迎访问我的GitHub

这里分类和汇总了欣宸的全部原创(含配套源码)：https://github.com/zq2599/blog_demos

关于《LeetCode买卖股票》系列

• 在LeetCode上，有数道和买卖股票有关的题目，覆盖了简单、中等、困难，要求都是选择低价时间买入、高价时间卖出，以求达到利润最大化
• 这类题型的特点就是：典型的动态规划题型，掌握套路后，越做越开心，就算难度是困难的题目，也能从容面对
• 于是，欣宸将此类题目聚集在一起，集中火力分析和解题，构成了《LeetCode买卖股票》系列，在该系列中，欣宸与您一同打好基础，再将该类型题目逐个攻克，在LeetCode世界中做一回股神

本篇概览

• 对之前的解题经历做了认真回顾后，我这边决定用第122题《买卖股票的最佳时机 II》作为系列的开篇，原因是此题在所有买卖股票的文章中最为典型：题目具备代表性，同时其他题目中奇怪的约束条件如冻结期、交易次数等，在122题中都不存在，写出的状态转移方程可以作为其他题目的参考
• 接下来开始做题吧，先看题目

题目信息

• 题号：122
• 难度：中等
• 描述

1. 给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。
2. 在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。
3. 返回 你能获得的 最大 利润 。

• 示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
     总利润为 4 + 3 = 7 。

• 示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     总利润为 4 。

• 示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

• 提示：

1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104

核心问题分析

• 解题的关键，是搞清楚两个最核心的问题：

1. 我们要的是什么？
2. 变化有哪些？

第一个问题：我们要的是什么？

• 认真审题后，我们要的东西可以这样描述：第i天股市结束后手里的最大利润

第二个问题：有哪些变化？

• 很容易发现，一共有两种变化：和行为无关、和行为有关

1. 和行为无关的变化：是时间和股价，只要知道是第几天，也就知道了股价，所以只要聚焦时间变化即可
2. 和行为有关的变化：股票持有情况，即持有和不持有

确定dp定义

• 弄清楚上述两个问题后，dp定义也就呼之欲出了：

1. dp数组的值就是我们想要的东西
2. dp数组的维度就是变化，一共有两个变化，所以一共有两个维度

• 于是，我们对dp数组的定义如下图
  
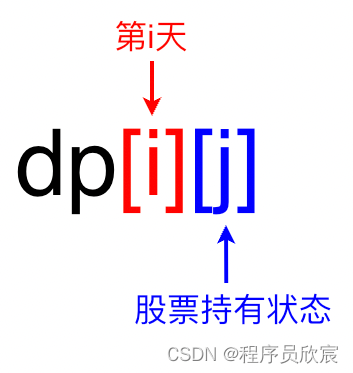
• 上图中，i的取值好理解，表示第几天，至于j，我们规定它只有两个值：0和1,0代表不持有股票，1代表持有股票
• 下图是个例子，很容易理解：第3天股市结束后，未持有股票时，手里的最大利润是123元
  

状态转移方程分析

• 要想写出状态转移方程，首先要弄明白状态是怎么变化的，时间状态自不必分析，它是客观在变化的，我们要弄明白的是另一个状态：股票持有状态，严格来说要弄清楚两点：

1. 第i天股市结束后，如果手里持有股票，这个股票是从哪来的？
2. 第i天股市结束后，如果手里没有股票，为什么手里会没有股票？

• 只要弄清楚上述两个问题，状态转移方程也就出来了，接下来逐个分析

手里持有股票的原因

• 第i天股市结束后，如果手里持有股票，有两种可能：

1. 第i天之前持有股票，到了第i天啥也不做，此时：dp[i][1]=dp[i-1][1]
2. 第i天之前不持有股票，在第i天购买了，此时：dp[i][1]=dp[i-1][0]-price[i]，因为购买要花钱，所以用手里的钱减去当天股价

• 我们要的是最大利润，所以应该取上述两种情况的最大值
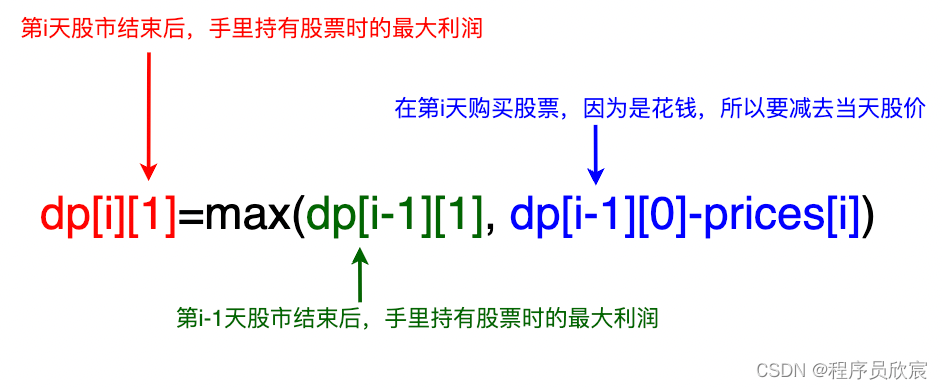
• 现在可以写出dp[i][1]的表达式了：dp[i][i]=Math.max(dp[i-1][1], dp[i-1][0]-price[i])
• 一图胜千言，看过下图您就一定明白了
  

手里未持有股票的原因

• 接下来继续分析，第i天股市结束后如果手里没有股票，有两种可能导致：

1. 第i天之前未持有股票，到了第i天啥也不做，此时：dp[i][0]=dp[i-1][0]
2. 第i天之前持有股票，在第i天卖出，此时：dp[i][0]=dp[i-1][1] + price[i]，因为卖出股票会换来钱，所以这里用手里的钱加上当天股价

• 我们要的是最大利润，所以应该取上述两种情况的最大值
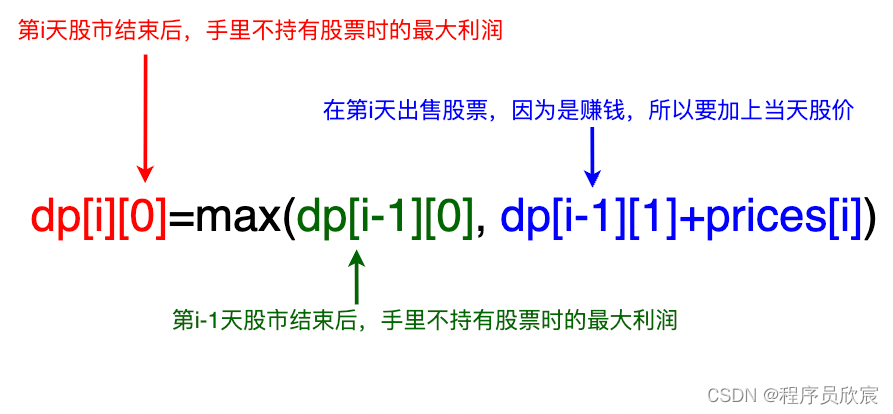
• 现在可以写出dp[i][0]的表达式了：dp[i][0]=Math.max(dp[i-1][0], dp[i-1][1]+price[i])
• 一图胜千言，看过下图您就一定明白了
  
• 状态转移方程已经出来了，接下来按部就班写好代码提交即可

编码

• 有了上面的分析，相信此刻您也能流畅的完成编码了，参考代码如下

class Solution {
    public int maxProfit(int[] prices) {

        int[][] dp = new int[prices.length][2];

        // 第0天股市结束后，如果手里没有股票，那就是没有购买过，此时最大利润只能等于0
        // 初始化为0的代码可以省去
        // dp[0][0] = 0;

        // 第0天股市结束后，如果手里有股票，那就是当前购买的，此时最大利润就是负数
        dp[0][1] = -prices[0];

        for (int i=1;i<prices.length;i++) {
        	// 第i天股市结束时，手里没有股票的原因有两个：
        	// 1. 之前就没有股票，第i天啥样没做
        	// 2. 之前有股票，第i天卖出
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            // 第i天股市结束时，手里有股票的原因有两个：
        	// 1. 之前就有股票，第i天啥样没做
        	// 2. 之前没有股票，第i天买入
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
        }

        // 第i天结束后，手里不持有股票的最大利润就是返回值
        return dp[prices.length-1][0];
    }
}

• 提交代码，如下所示，虽然AC了，但是速度很一般，超过26.27%的提交，显然还有优化空间
  

优化

• 回顾上述代码中，dp[i][0]和dp[i][1]都是通过dp[i-i][0]和dp[i-1][1]计算出来的，如此看来，这个dp二维数组似乎有些浪费，用下面这四个变量足矣

1. prevWithStock：前一天股市结束后，手里有股票时的最大利润
2. prevWithoutStock：前一天股市结束后，手里没有股票时的最大利润
3. currentWithStock：当天股市结束后，手里有股票时的最大利润
4. currentWithoutStock：当天股市结束后，手里没有股票时的最大利润

• 优化后的代码如下

class Solution {
    public int maxProfit(int[] prices) {
        // 第0天股市结束后，如果手里有股票，那就是当前购买的，此时最大利润就是负数
        int prevWithStock = -prices[0];

        // 第0天股市结束后，如果手里没有股票，那就是没有购买过，此时最大利润只能等于0
        int prevWithoutStock = 0;

        // 当天股市结束后，如果手里有股票时的最大利润
        int currentWithStock;

        // 当天股市结束后，如果手里没有股票时的最大利润
        int currentWithoutStock = 0;
        
        for (int i=1;i<prices.length;i++) {
            currentWithoutStock = Math.max(prevWithoutStock, prevWithStock + prices[i]);
            currentWithStock = Math.max(prevWithStock, prevWithoutStock - prices[i]);
            prevWithStock = currentWithStock;
            prevWithoutStock = currentWithoutStock;
        }

        // 第i天结束后，手里不持有股票的最大利润就是返回值
        return currentWithoutStock;
    }
}

• 再次提交，稍微提升了一点
  
• 至此，买卖股票的基本套路，以及状态转移方程设计思路和实现，咱们已经学习到了，接下来的文章中，都会基于这个思路去设置状态转移方程
• 当然了，此刻您应该还有个疑问：为何速度的排名如此之低？接下来咱们来看看落后的原因

为啥排名不高？

• 这道题本身也有一些特殊：除了动态规划，贪心算法也能解
• 以prices={1, 2, 3}为例，聪明的您应该看出来了，如果1买入，3卖出，得到的利润等于2，属于最大利润
• 题目有个约束：一天不能既买入又卖出，如果跳出这个约束，那就可以做到1买入2卖出，然后2买入3卖出，利润还是2！
• 至于能不能将3-1转化成(3-2)+(2-1)呢？当然可以，减去2再加上2，对原题的结果毫无影响，却可以改变代码流程，如下所示，每当买入卖出能赚钱时，就将插件累加起来，这样的计算中，相比前面的代码，每次循环中的计算量明显减少了

class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length<2) {
            return 0;
        }

        int total = 0;

        for (int i=1;i<prices.length;i++) {

            if (prices[i]>prices[i-1]) {
                total += prices[i] - prices[i-1];
            }

        }

        return total;
    }
}

• 再次提交，这回超越了百分百
  
• 至此又得出一个结论：本题用动态规划做并没有错，也不是动态规划代码没写好，而是有更高效的贪心算法恰巧也能解决此问题
• 经过本篇实战，相信您对动态规划以及股票买卖问题都有了更深的理解，接下来，继续挑战其他股票买卖问题，在LeetCode世界中向着股神前进

欢迎关注博客园：程序员欣宸

学习路上，你不孤单，欣宸原创一路相伴...