图像处理与Python实现（岳亚伟）笔记四——频域滤波
为了更加有效的对数字图像进行处理，常常需要将原始图像以某种方式变换到另外一个空间，并利用图像在变换空间中的特有性质对图像信息进行加工，然后再转换回图像空间就可以得到所需的效果。图像变换是双向的，一般将从图像控件转换到其他空间的操作称为正变换，由其他空间转换回图像空间称为逆变换。
傅里叶变换可以将任何周期函数分解为不同频率的信号成分。频域变换为信号处理提供了不同的思路，有时在空间域无法处理的问题，通过频域变换却变得非常容易。
傅里叶变换中将图像看作二维信号，其水平方向和垂直方向作为二维空间的坐标轴，将图像本身所在的域称为空间域。图像灰度值随空间坐标变换的节奏可以通过频率度娘，称为空间频率或者频域。针对数字图像的傅里叶变换是将原始图像通过傅里叶变换转换到频域，然后在频域中对图像进行处理的方法。基于傅里叶变换的数字图像频域处理过程如图1所示
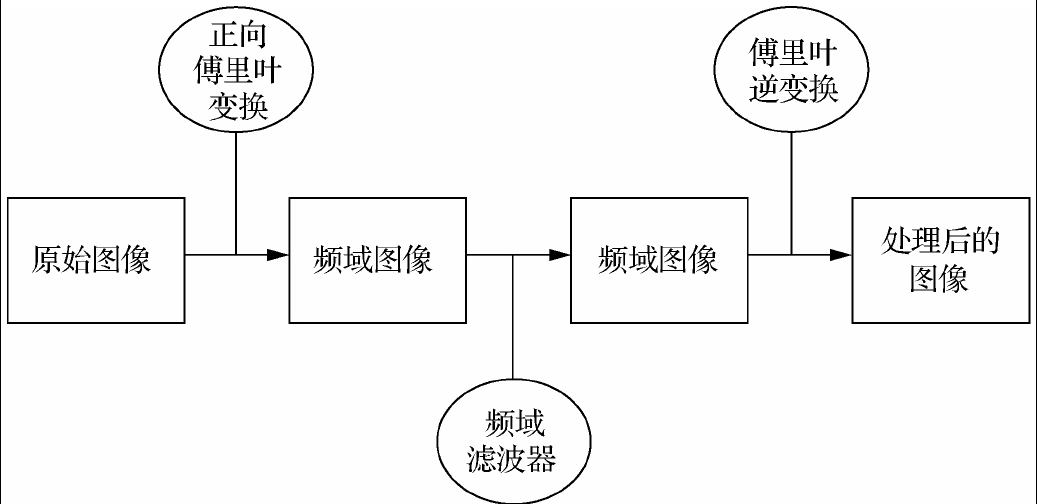
图1，基于傅里叶变换的数字图像品预处理过程
首先通过正向傅里叶变换将原始图像从空间域转换到频域。然后使用频域滤波器将某些频率成分过滤掉，保留某些特定频率。最后使用傅里叶逆变换将滤波后的频域图像重新转换到空间域，得到处理后的图像。
相较于图像空间域处理，频域图像处理有以下优点：1）频域图像处理可以通过频域成分的特殊性质完成一些空间域图像处理难以完成的任务。2）频域图像处理更有利于信号处理的解释，它可以对滤波过程中产生的某些效果做出比较直观的解释。3）频域滤波器可以作为空间滤波器设计的知道，通过傅里叶逆变换可以将频域滤波器转换为空间域变换的操作。通过频域滤波做前期设计，然后实施阶段用空间域滤波实现。
一，傅里叶变换
傅里叶变换是一种常见的正交数学变换，可以将一维信号或函数分解为具有不同频率、不同幅度的正弦信号或余弦信号的组合。傅里叶分析中最重要的结论是几乎“所有”信号或函数都可以分解成简单的正弦波和余弦波之和，从而提供了一种具有物理意义的函数表达方式。傅里叶变换的核心贡献在于：1）如何求出每种正弦波和余弦波的比例（频率）；2）给定每种正弦波和余弦波的比例，可以恢复出原始信号。
1.1 一维傅里叶变换
一个函数的傅里叶变换可以表示为：
$F(u) = \int_{-\infty }^{\infty } f(x)e^{-j2\pi u x}dx$
其对应的傅里叶逆变换表示为：
$f(x) = \int_{-\infty }^{\infty } F(u)e^{j2\pi u x}du$，其中$j=\sqrt{-1}$, u为频率分量。
傅里叶变换中基函数的物理意义非常明确，每个基函数都是一个但频率谐波，对应的系数（又称频谱）表明了原函数在此基函数投影的大小，或者也可以看作原函数中此种频率谐波成分的比重。实际应用中需要求解的更多问题是离散信号的处理，定义离散情况的傅里叶变换公式$f(x)$，其中$x=0,1,...,M-1$，则其傅里叶正变换为：
$F(u)=\sum_{x=0}^{M-1}f(x)e^{-j2 \pi ux/M}, u=0,1,...,M-1$
傅里叶逆变换为：
$f(x)=\frac{1}{M}\sum_{u=0}^{M-1}F(u)e^{j2 \pi ux/M}, x=0,1,...,M-1$
观察傅里叶逆变换，通过欧拉公式$e^{j\Theta }=cos\Theta + jsin\Theta $可得：
$f(x)=\frac{1}{M}\sum_{u=0}^{M-1}F(u)e^{j2 \pi ux/M}=\frac{1}{M}\sum_{u=0}^{M-1}F(u)[cos(2 \pi ux/M)+jsin(2 \pi ux/M)]$
可以看到，空间域函数$f(x)$可表示为M个正弦（余弦）函数的累加，其中$F(u)/M$为对应频率分量的幅度（系数）。$F(u)$覆盖的域（即u值得取值范围）称为频域。令$u=0$，可得$F(0)=\frac{1}{M}\sum_{x=0}^{M-1}f(x)$, $F(0)$对应$f(x)$的均值，又可称为直流分量。其余u值对应的的$F(u)$则成为$f(x)$的交流分量。通过变量u可以确定变换后的频率成分，而u的取值范围称为频域。对每个u值，其对应的$F(u)$称为傅里叶变换的频率分量（或称振幅）。
可以注意到傅里叶变换后的函数是在复数域内，又可以表示为$F(u)=R(u)+jI(u)$，或者以极坐标的形式表示为$F(u)=\left | F(u) \right |e^{\psi (u)}$。这里把$\left | F(u) \right |=\left [ R^{2}(u)+I^{2}(u) \right ]^{1/2}$称为傅里叶变换的幅度或者谱。通过谱可以表示原函数（或图像）对某一频谱分量的贡献。$\phi (u)=arctan\left [ \frac{I(u)}{R(u)} \right ]$称为变换的相位角或相位谱，用来表示原函数中某一频谱分量的起始位置。谱的平方称为功率谱（也叫能量谱，谱密度），表示为$P(u)=F^2(u)=R^2(u)+I^2(u)$。
ps: 傅里叶变换后，如何确定每个点的频率值：
计算方法：
- 对离散信号S进行FFT变换，方法很多，一个函数而已。
- 定义采样频率Fs，（每年监测多少期）
- 用采样频率计算监测信号中周期个数：
Tn= N/FsTn=N/Fs
式中，N 为时序 S 的长度 。 - 确定每个点对应的频率
w= K/Tnw=K/Tn
式中，K 为时序S对应的自然数序列，从 0 到 N-1 的自然数序列。
1.2 二维傅里叶变换
二维傅里叶变换本质上是将一维傅里叶变换清醒向二维进行简单扩展：
$F(u, v) = \int_{-\infty }^{\infty } \int_{-\infty }^{\infty } f(x, y)e^{-j2\pi (ux+vy)}dxdy$，对应二维傅里叶变换的逆变换可以表示为：$f(x,y) =\int_{-\infty }^{\infty } \int_{-\infty }^{\infty } F(u, v)e^{j2\pi (ux+vy)}dudv$
离散情形完全与连续形式类似，设$f(x, y)$是一幅尺寸为$M \times N$的图像函数，相应的二维离散傅里叶变换可以表示为：
$F(u, v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2 \pi (ux/M+vy/N)}, u=0,1,...,M-1; v=0,1,...,N-1$
u，v均为频率分量。通过傅里叶变换$F(u, v)$失去了空间关系，只保留了频率关系。其中空间域是由$f(x,y)$所张成的坐标系，x和y是变量。而频域则是由$F(u, v)$所张成的坐标系，u和v是变量。u和v定义的矩形区域称为频率矩形，其大小与图像$f(x, y)$的大小相同。$F(u, v)$是傅里叶系数。该图像函数对应的傅里叶逆变换可以表示为：
$f(x, y)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}F(u,v)e^{j2 \pi (ux/M+vy/N)}, u=0,1,...,M-1; v=0,1,...,N-1$
二，傅里叶变换的性质
2.1 傅里叶变换的基本性质
1，线性特性：若$f(t)<--->F(\Omega ), g(t)<--->G(\Omega )$ 则 $af(t)+bg(t)<--->aF(\Omega )+bG(\Omega )$，其中$a, b$为任意常数，利用傅里叶变换的线性特性，可以将待求信号分解为若干基本信号之和。
2，时延特性：傅里叶变换的时延（移位）特性可以表示为：若$f(t)<--->F(\Omega )$，则$f1(t)=f(t-t0)<--->F1(\Omega )=F(\Omega )e^{-j\Omega t0}$。时延特性说明波形在时间轴上时延，并不会改变信号幅度，仅使信号增加$-\Omega t0$线性相位。
3，频移特性：傅里叶变换的频移（调制）特性表示为：若$f(t)<-->F(\Omega )$，则$f(t)e^{j\Omega_{0} t}<--->F(\Omega - \Omega _{0})$，频移特性表明信号在时域中与复因子$e^{j\Omega _{0}t}$相乘，则在频域中使整个频谱搬移$\Omega _{0}$
4, 尺度变换: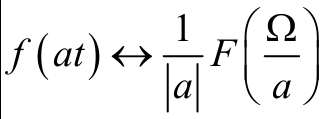 
，如图2所示
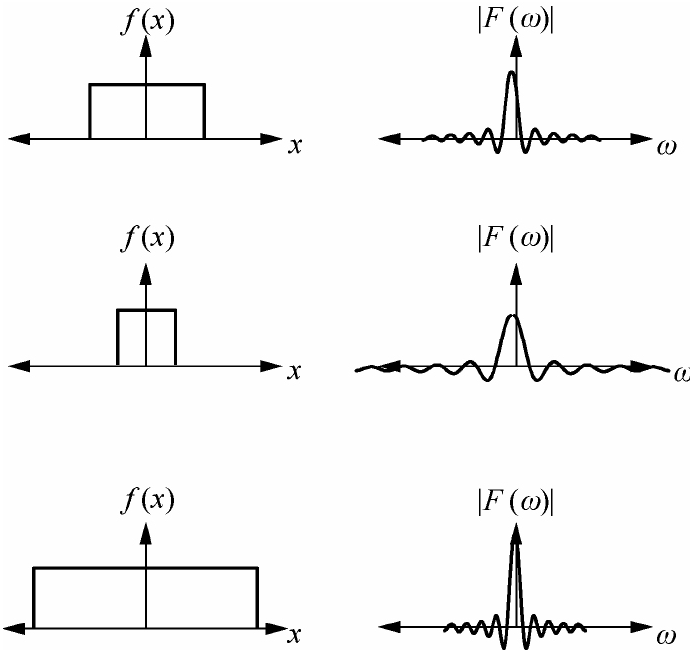
图2
尺度特性说明，信号在时域中压缩，在频域中扩展；反之，信号在时域中扩展，在频域中就一定压缩；即信号的脉宽与带宽成反比。一般来说，时宽有限的信号，其频宽无限，反之亦然。可以理解为信号波形压缩为1/a或扩展a倍，信号随时间变化的岁都加快a倍或减慢为1/a，所以信号包含的频率分量增加a倍或减少为1/a。频谱展宽a倍或压缩为1/a。又因能量守恒原理，各频率分量的大小减小为1/a或增加a倍。
5，时域微分特性
若$f(t)<--->F(\Omega)$，则$\frac{df(t)}{dt}<--->j\Omega F(\Omega)$
同理，可推广到高阶导数的傅里叶变换：$\frac{df^n(t)}{dt^n}<--->(j\Omega)^nF(\Omega)$
6, 频域微分特性
若$f(t)<--->F(\Omega)$，则$\frac{dF(\Omega)}{d\Omega} <---> (-jt)f(t)$
一般频域微分特性的实用形式为 $j\frac{dF(\Omega)}{d \Omega} <--->tf(t)$，对频谱函数的高阶导数也成立，即
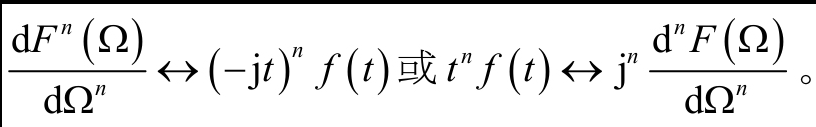
7，对称（偶）性
傅里叶变换的对称性表示为：若$f(t)<--->F(\Omega)$，则$F(t)<--->2 \pi f(-\Omega)$ 或 $\frac{1}{2 \pi}F(t)<--->f(- \Omega)$
8，时域卷积定理
傅里叶变换的始于卷积定理表示为：若$f_1(t)<--->F_1(\Omega), f_2(\Omega)<--->F_2(t)$, 则$f_1(t)*f_2(t)<--->F_1(\Omega)F_2(\Omega)$
9，频域卷积定理
傅里叶变换的频域卷积定理表示为：若$f_1(t)<--->F_1(\Omega), f_2(t)<--->F_2(\Omega)$，则$f_1(t)f_2(t)<--->\frac{1}{2 \pi}F_1(\Omega)*F_2(\Omega)$
2.2 二维傅里叶变换的性质
相较于一维傅里叶变换，二维傅里叶变换还具有可分离性、平移特性、旋转特性等特性。
1，可分离性
二维离散傅里叶变换（DFT）可视为由沿x, y方向的两个一维傅里叶变换所构成。这一性质可以有效降低二位傅里叶变换的计算复杂性。如
$F(u, v)=\frac{1}{N^2}\sum_{x=0}^{N-1}e^{-j2 \pi ux/N}\cdot \sum_{y=0}^{N-1}f(x,y)e^{-j2 \pi vy/N}$
傅里叶逆变换也可以进行分离：
$f(x, y) = \sum_{u=0}^{N-1}e^{-j2 \pi ux/N} \cdot \sum_{v=0}^{N-1}F(u, v)e^{-j2 \pi vy/N}$
这样，原本在$O_{xy}$或$O_{uv}$平面需要$O(N^2)$时间复杂度才可以完成的操作，经过分离之后可以由x和y方向的两次时间复杂度为O(N)的一维傅里叶变换操作代替。逆变换同理。
2，平移特性，二维傅里叶变换的平移特性表示如下：
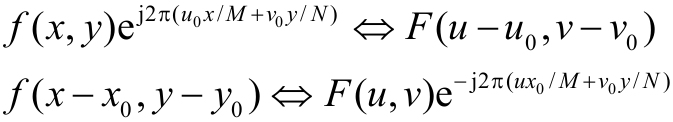
f(x,y)在空间平移了，相当于把傅里叶变换与一个指数相乘。f(x,y)在空间与一个指数项相乘，相当于平移其傅里叶变换。当$u_0=M/2, v_0=N/2$时，
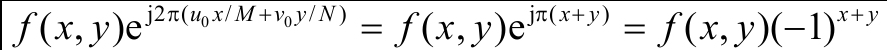
通常，在变换前用$(-1)^{x+y}$乘以输入图像函数，实现频域中心化变换：
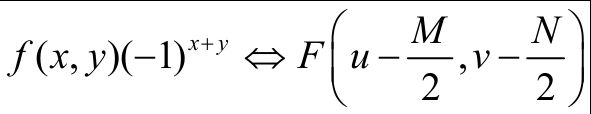
3，旋转特性
对f(x,y)旋转一定角度，相当于将其傅里叶变换F(u, v)旋转一定角度。
四，图像频域滤波
图像变换是对图像信息进行变换，使能量保持但重新分配，以利于加工、处理（滤除不必要信息，如噪声，加强、提取感兴趣的部分或特征）。傅里叶变换在图像分析，滤波，增强，压缩等处理中有非常重要的应用。
假定原图像$f(x,y)$经傅里叶变换为$F(u,v)$，频域增强就是选择合适的滤波器函数$H(u,v)$对$F(u,v)$的频谱成分进行调整，然后经傅里叶变换得到增强的图像$g(x,y)$。该过程可以通过下面的流程描述：
其中，$G(u,v)=H(u, v) \cdot F(u,v)$, H(u, v)称为传递函数或滤波器函数。
可以选择合适的频率传递函数H(u,v)突出f(x,y)某一方面的特征，从而得到需要的图像g(x,y)。例如，利用传递函数H(u,v)突出高频分量，以增强图像的边缘信息，即高通滤波；如果突出低频分量，就可以使图像显得比较平滑，即低通滤波。
频域滤波的基本步骤如下：
（1）对原始图像$f(x,y)$进行傅里叶变换得到F(u,v).
（2）将F(u,v)与传递函数H(u,v)进行卷积运算得到G(u,v)
（3）将G(u,v)进行傅里叶变换得到增强图像g(x,y)。频域滤波的核心在于如何确定传递函数，即H(u,v)
4.1 低通滤波
图像从空间域变换到频域后，其低频分量对应图像中灰度值变化比较缓慢的区域，高频分量则表征图像中物体的边缘和随机噪声等信息。低通滤波是指保留低频分量，而通过滤波器函数H(u,v)减弱或抑制高频分量在频域进行的滤波。低通滤波与空间域中的平滑滤波器一样，可以消除图象中的随机噪声，减弱边缘效应，起到平滑图像的作用。
4.1.1 理想低通滤波器
二维理想低通滤波器的传递函数如下，二维理想低通滤波器的传递函数如下：
$H(u,v)=\left\{\begin{matrix}
1 & D(u,v)\leqslant D_0\\
0& D(u,v)> D_0
\end{matrix}\right.$
阶段频率$D_0$是一个非负整数，$D(u,v)$是从点$(u,v)$到频率平面原点的距离，即$D(u,v)=\sqrt{u^2+v^2}$。理想低通滤波器的含义是指小于$D_0$的频率，即以$D_0$为半径的圆内的所有频率分量可以完全无损的通过，而圆外的频率，即大于$D_0$的频率分量则完全被除掉。理想低通滤波器的平滑作用非常明显，但由于变换有一个陡峭的波形，它的逆变换$h(x,y)$有强烈的振铃特性，使滤波后的图像产生模糊效果。因此，这种理想低通滤波器在实际中并不采用。理想低通滤波器的傅里叶变换结果如图3所示
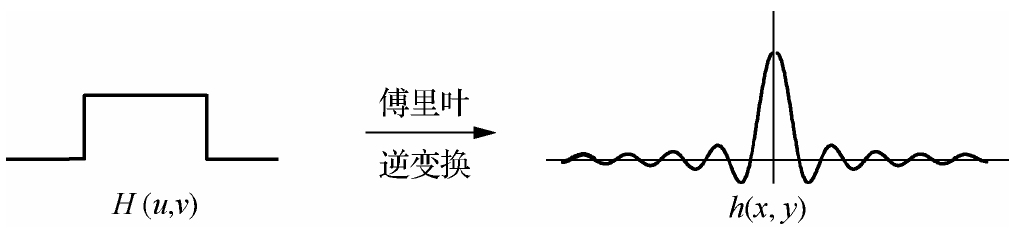
图3，理想低通滤波器的傅里叶逆变换结果
二维理想低通滤波器结果如图4所示：
图4，二维图像的理想低通滤波结果
理想低通滤波器在数学上定义得很清楚，在计算机模拟中也可实现，但在截断频率处，直上直下的理想低通滤波器不能用实际的电子器件实现，物理上可实现的是Butterworth（巴特沃斯）低通滤波器。
4.1.2 Butterworth低通滤波器
Butterworth低通滤波器的传递函数为：
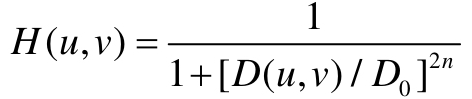
$D_0$为截至频率，n为函数的阶。一般取使$H(u,v)$最大值下降到最大值的一半时的$D(u,v)$为截止频率$D_0$。Butterworth低通滤波器截面图如图5所示：
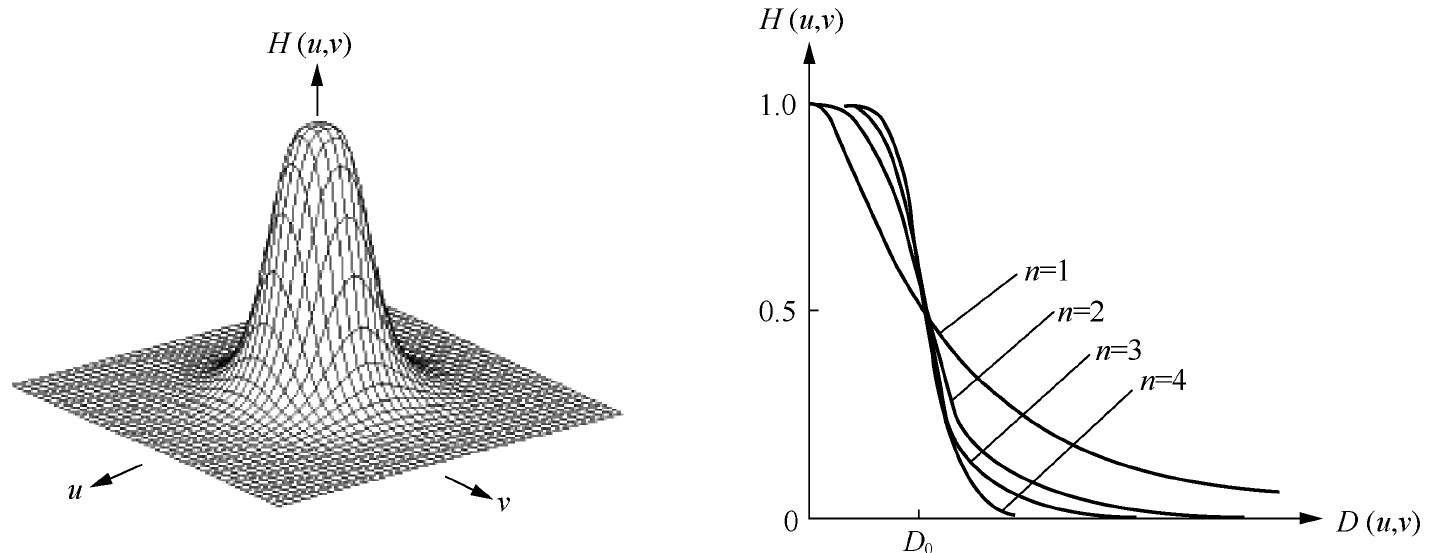
图5，Butterworth低通滤波器的截面
与理想低通滤波器相比，高低频之间过渡较为平滑，用此滤波后的输出图像振铃现象不明显。n=1时，过渡最为平滑，即尾部包含大量的高频成分，所以一阶Butterworth低通滤波器没有振铃现象；但随着n的增加，振铃现象会越来越明显。
4.2 高通滤波
图像的边缘、细节主要在高频，图像模糊的原因是高频成分较弱。为了消除模糊，突出边缘，可以采用高通滤波的方法，使低频分量得到抑制，从而达到增强高频分量，使图像的边缘或线条变得清晰，实现图像的锐化。
4.2.1 理想高通滤波器
理想高通滤波器的形状与低通滤波器的形状正好相反，其传递函数为：
$H(u,v)=\left\{\begin{matrix}
0 & D(u,v)\leqslant D_0\\
1& D(u,v)> D_0
\end{matrix}\right.$
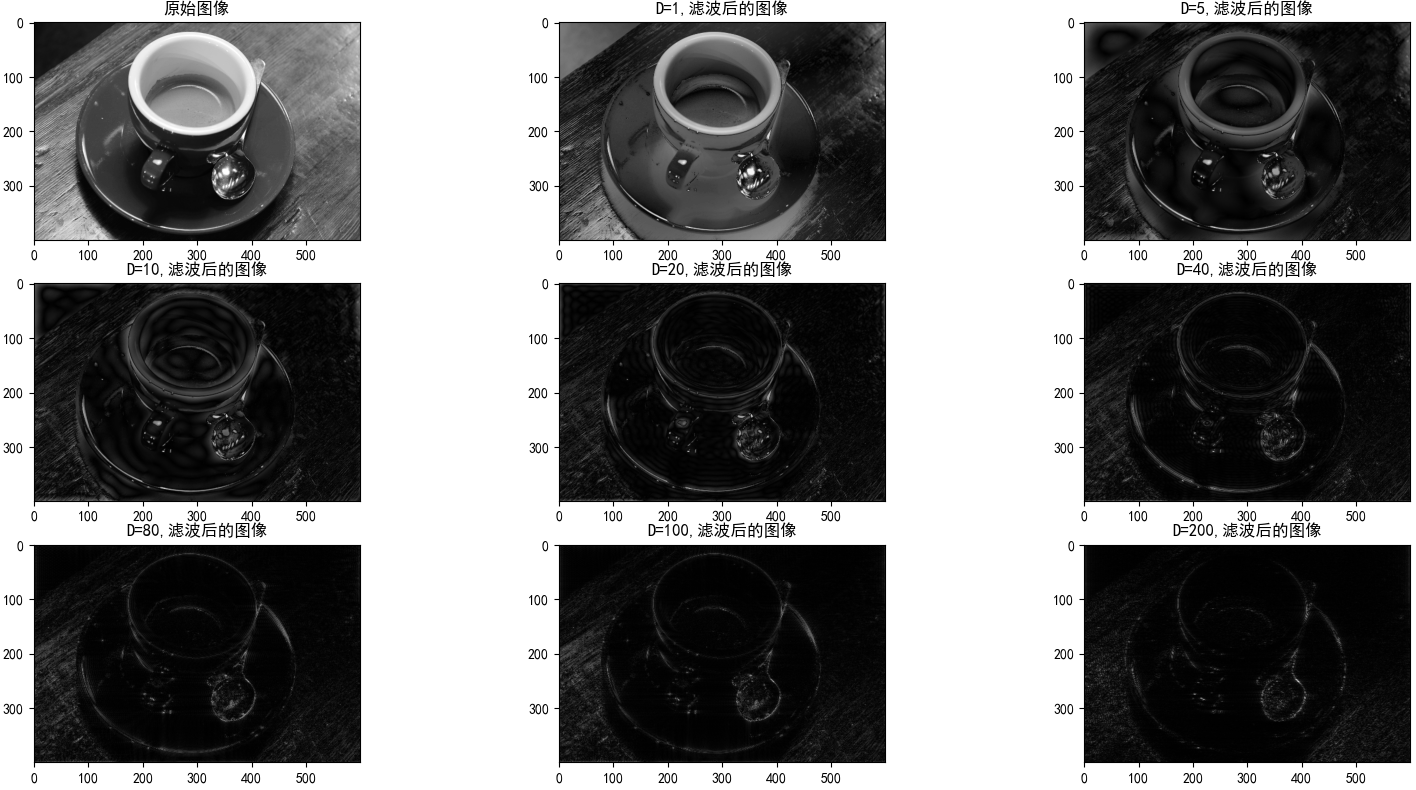
图6，二维图像的理想高通滤波结果
4.2.2 Butterworth高通滤波器
Butterworth高通滤波器的形状与Butterworth低通滤波器相反，同样，因为高低频率间平滑过渡，因此振铃现象不明显。其传递函数如下：
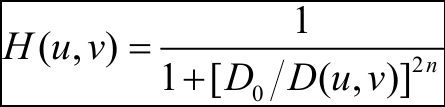
图7，二维图像Butterworth高通滤波结果
4.2.3 高频增强滤波器
高通滤波将低频分量滤掉，导致增强途中的边缘得到加强，但平坦区域灰度很暗，接近黑色。高频增强滤波器对频域率的高通滤波器的转移函数加一个常数，以将一些低频分量加回去，既保持光滑区域灰度，又改善边缘区域对比度。高频增强转移函数
$H_e(u,v) = kH(u, v)+c$
这样就可以做到在原始图像的基础上叠加一些高频成分，既保留了原图的灰度层次，又锐化了边缘。
