平方-乘算法与Miller-Rabin素性测试算法
平方-乘算法
代码实现
a=19244;h=17;n=221
a=input("a^h(mod n)\na");h=input("h");n=input("n")
h=int(h);a=int(a);n=int(n)
H=bin(h)
z=a
#print(a,'----',H[2])
for i in range(3,H.__len__()):
if(H[i]=='1'):
a=(a*a)%n
a=(a*z)%n
if(H[i]=='0'):
a=(a*a)%n
print(a)
测试用例
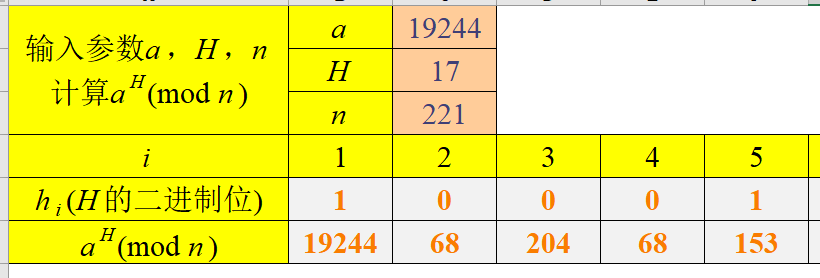

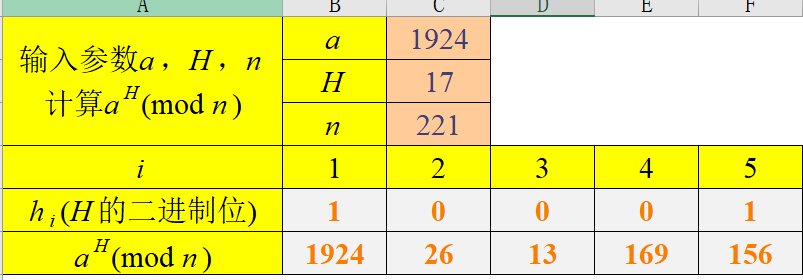

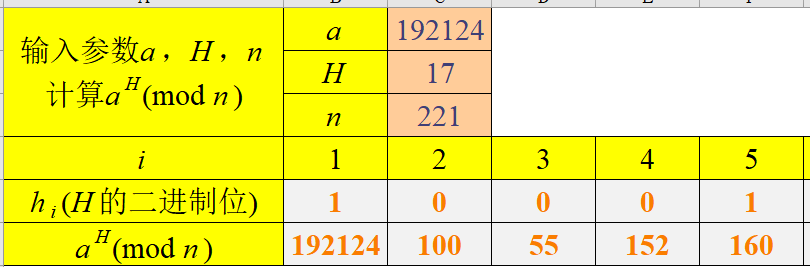

Miller-Rabin素性测试算法
代码实现
#include <iostream>
#include <cmath>
using namespace std;
int modpow(int base, int exp, int mod) {
int cnt = 1;
base %= mod;
while (exp > 0) {
if (exp % 2 == 1) {
cnt = (cnt * base) % mod;
}
exp >>= 1;
base = (base * base) % mod;
}
return cnt;
}
bool MR(int n, int a) {
if (n <= 1 || n == 4) {
return false;
}
if (n <= 3) {
return true;
}
int d = n - 1;
while (d % 2 == 0) {
d /= 2;
}
int x = modpow(a, d, n);
if (x == 1 || x == n - 1) {
return true;
}
while (d != n - 1) {
x = (x * x) % n;
d *= 2;
if (x == 1) {
return false;
}
if (x == n - 1) {
return true;
}
}
return false;
}
int main() {
int n, a;
n=2017,a=19;
cout<<"待测正整数为"<<n<<" 基数为"<<a<<endl;
//cin >> n >> a;
if (MR(n, a)) {
cout << n << " 是素数" << endl;
} else {
cout << n << " 不是素数" << endl;
}
return 0;
}
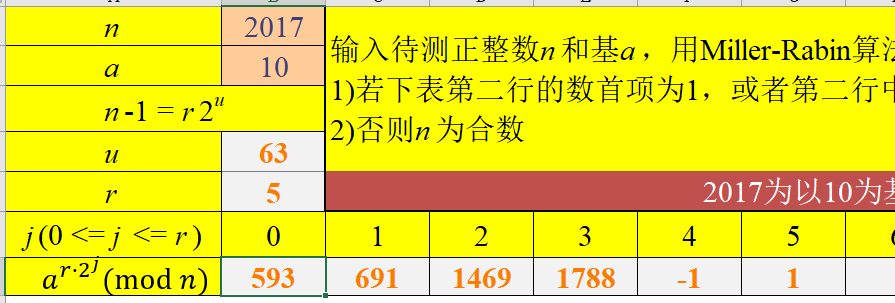
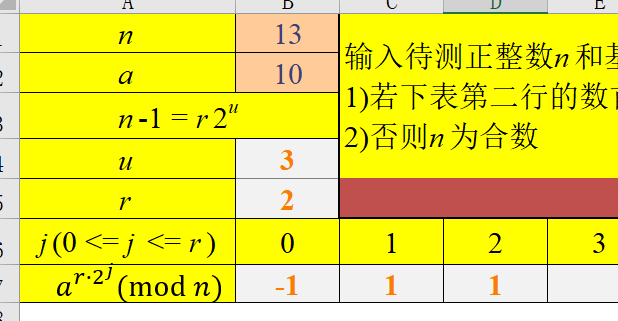
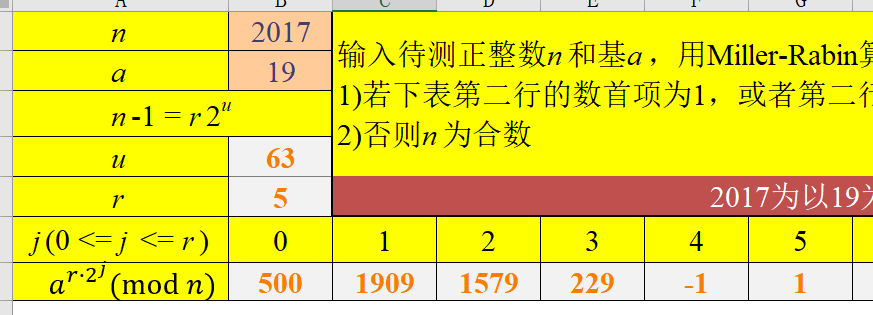
测试用例














 浙公网安备 33010602011771号
浙公网安备 33010602011771号