EEA与CRT
Public-Key Cryptography
EEA 拓展欧几里得算法
算法实现
#include<bits/stdc++.h>
using namespace std;
int t1,t0,q,tem;
int eea(int a,int m){//a>m
if(a==0 || m==0)return t0;
else{
q=a/m;
tem=m;
m=a%m;
a=tem;
tem=t1;
t1=t0-q*t1;
t0=tem;
// cout<<a<<' '<<m<<' '<<q<<' '<<t0<<endl;
eea(a,m);
}
}
int gcd(int a, int b)
{
if(b == 0)return a;
else return gcd(b , a % b);
}
int main()
{
int a,m;
a=243,m=199;
//cin>>a>>m;
//a*s+m*t=(a,m)
cout<<"最大公约数为"<<gcd(a,m)<<endl;
t1=1,t0=0;
int esum=eea(a,m);
cout<<"乘法逆元s为"<<esum<<endl;
t1=1,t0=0;
esum=eea(m,a);
cout<<"乘法逆元t为"<<esum;
return 0;
}
测试样例
3个测试用例截图,乘法逆元皆为s,但是以上程序输出既有乘法逆元s也有t:
-
243 199

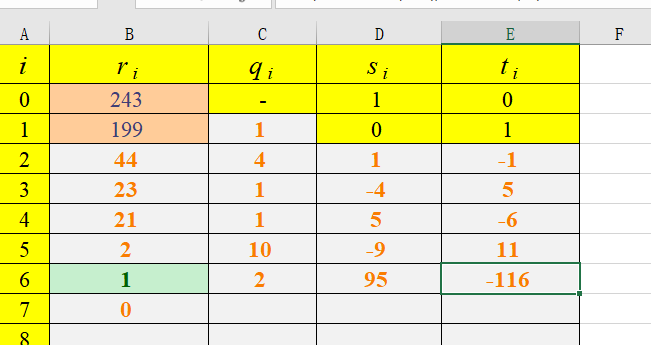
-
15 7

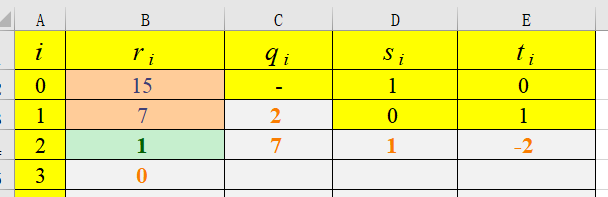
-
67 32

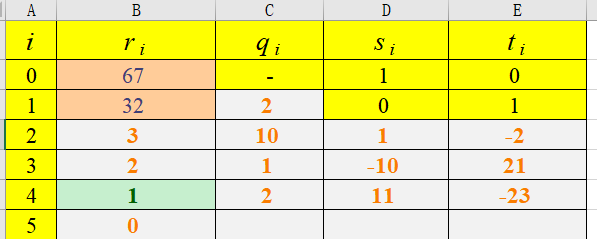
CRT 中国剩余定理
算法实现
#include<bits/stdc++.h>
using namespace std;
int t1,t0,q,tem;
int eea(int a,int m){
if(a==0 || m==0)return t0;
else{
q=a/m;
tem=m;
m=a%m;
a=tem;
tem=t1;
t1=t0-q*t1;
t0=tem;
//cout<<a<<' '<<' '<<q<<' '<<t0<<endl;
eea(a,m);
}
}
int gcd(int a, int b)
{
if(b == 0)return a;
else return gcd(b , a % b);
}
int main()
{
int k,x=0,flag,msum=1,M[11],M1[11];
k=4;
int b[11]={1,2,4,3};
int m[11]={4,5,7,9};
// cin>>k;
// for(int i=0;i<k;i++)cin>>b[i];
// for(int i=0;i<k;i++)cin>>m[i],msum*=m[i];
for(int i=0;i<k;i++)msum*=m[i];
for(int i=0;i<k;i++)M[i]=msum/m[i];
for(int i=0;i<k;i++){
flag=gcd(M[i],m[i]);
if(flag>1){cout<<"参数无效";return 0;}
else{
t1=1,t0=0;
M1[i]=eea(m[i],M[i]);
//cout<<endl;
// cout<<"M "<<M[i]<<" mi "<<m[i]<<" m "<<msum<<" M1 "<<M1[i]<<endl;
}
}
for(int i=0;i<k;i++)x+=((M1[i]*M[i]*b[i])%msum);
cout<<"同余方程组的解x≡"<<x<<"(mod"<<msum<<")";
return 0;
}
测试样例
3个测试用例截图
-
4 1 2 4 3 4 5 7 9

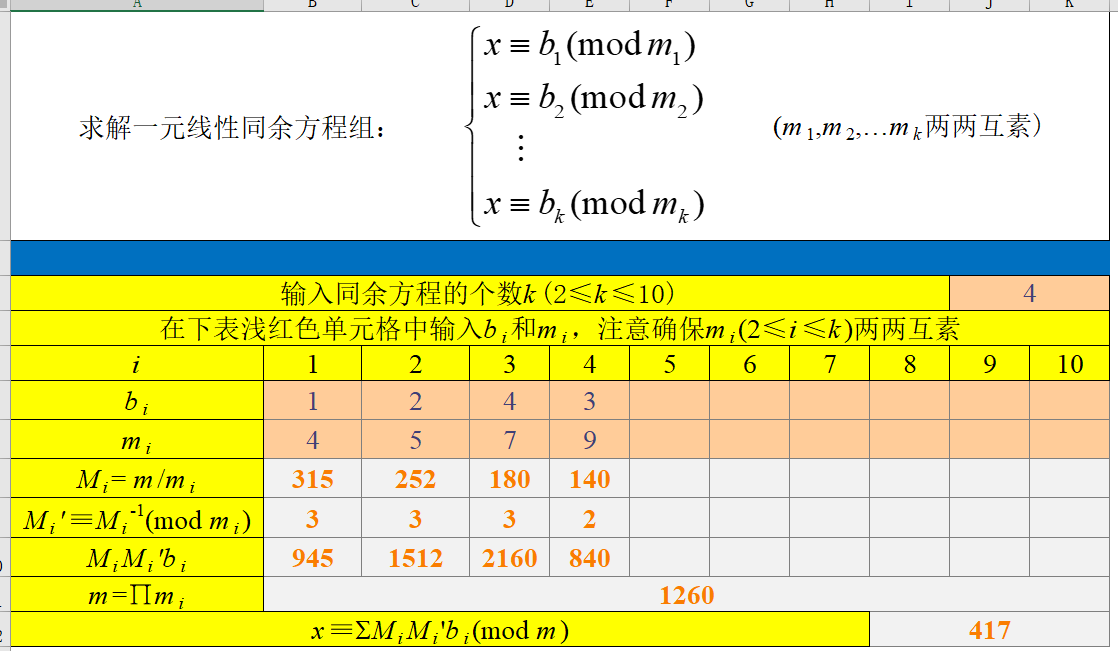
-
5 1 2 4 3 2 4 5 7 9 5
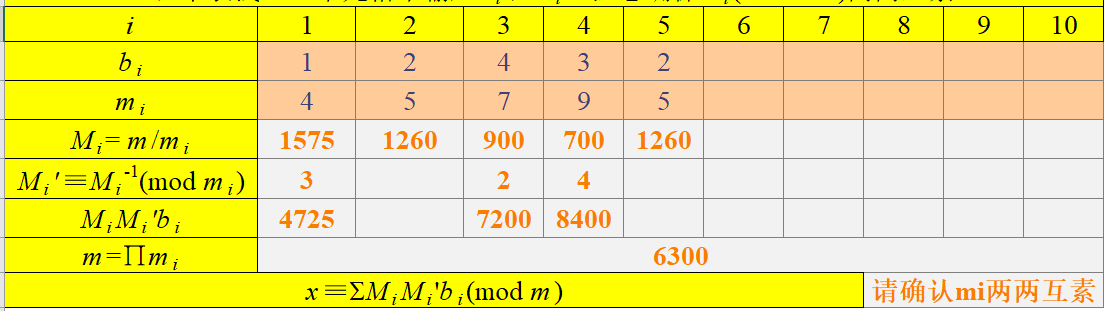
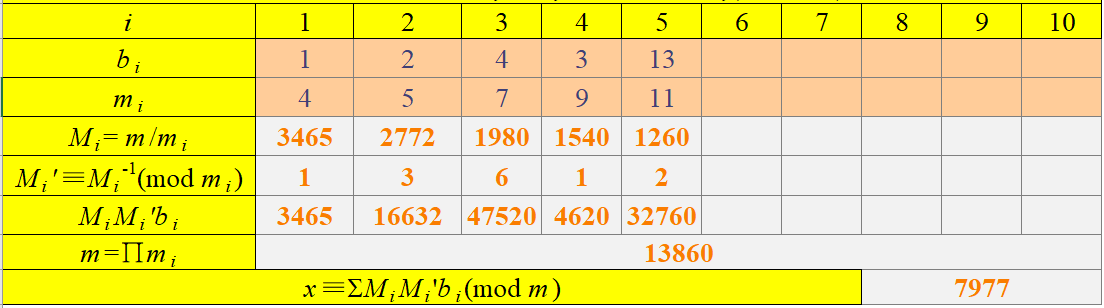
-
5 1 2 4 3 13 4 5 7 9 11



 浙公网安备 33010602011771号
浙公网安备 33010602011771号