SPOJ SAMER08A - Almost Shortest Path

题目链接：http://www.spoj.com/problems/SAMER08A/

题目大意：给出一个有向图，让你求一条S到D的几乎最短的路。要求是这条路上任意两个节点不属于任何一条最短路。N个点，M条边。 2 ≤ N ≤ 500  1 ≤ M≤ 104

解题思路：可以首先确定对于点i来说，与之相邻的哪个节点是不能选择的。之后再在这个基础上跑最短路就行。所以，可以首先对原图跑dijk找到S到任意一个点的最短路长度，再对反向图跑dijk找到任意一个点到D的最短路的长度。然后枚举每个点以及与之共享边的点，判断这两个点dis(S,i) + dis(j, D) + w是否与最短路长度相等，即这条边是否在一条最短路上，然后用set记录下每个节点i的不可选的节点。再跑一遍dijk就行。最后一遍dijk的时候要注意对每个点，不能选其set中已记录的点。

代码：

  1 const int inf = 0x3f3f3f3f;
  2 const int maxn = 2e5 + 5;
  3 const int maxm = 1e4 + 100;
  4 struct Edge{
  5     int to, next, val;
  6 };
  7 Edge edges[maxm], edges1[maxn];
  8 int tot, head[maxn], tot1, head1[maxn];
  9 int n, m, s, d;
 10 set<int> a[maxn];
 11 bool vis[maxn];
 12 int dis[maxn], dis1[maxn], dis2[maxn];
 13 
 14 void init(){
 15     tot = 0; tot1 = 0;
 16     memset(head, -1, sizeof(head));
 17     memset(head1, -1, sizeof(head1));
 18 }
 19 void addEdge(int u, int v, int w){
 20     edges[tot].to = v;
 21     edges[tot].val = w;
 22     edges[tot].next = head[u];
 23     head[u] = tot++;
 24 }
 25 void addEdge1(int u, int v, int w){
 26     edges1[tot1].to = v;
 27     edges1[tot1].val = w;
 28     edges1[tot1].next = head1[u];
 29     head1[u] = tot1++;
 30 }
 31 priority_queue<PII, vector<PII>, greater<PII> > q;
 32 void dijk(){
 33     while(!q.empty()) q.pop();
 34     memset(vis, 0, sizeof(vis));
 35     memset(dis, 0x3f, sizeof(dis));
 36     dis[s] = 0;
 37     q.push(PII(0, s));
 38     while(!q.empty()){
 39         int u = q.top().second; q.pop();
 40         if(u == d) return;
 41         if(vis[u]) continue;
 42         vis[u] = 1;
 43         for(int i = head[u]; i != -1; i = edges[i].next){
 44             int v = edges[i].to, w = edges[i].val;
 45             if(a[u].find(v) != a[u].end()) continue;
 46             if(dis[v] > dis[u] + w){
 47                 dis[v] = dis[u] + w;
 48                 q.push(PII(dis[v], v));
 49             }
 50         }
 51     }
 52 }
 53 void dijk1(){
 54     while(!q.empty()) q.pop();
 55     memset(vis, 0, sizeof(vis));
 56     memset(dis1, 0x3f, sizeof(dis1));
 57     dis1[s] = 0;
 58     q.push(PII(0, s));
 59     while(!q.empty()){
 60         int u = q.top().second; q.pop();
 61         if(vis[u]) continue;
 62         vis[u] = 1;
 63         for(int i = head[u]; i != -1; i = edges[i].next){
 64             int v = edges[i].to, w = edges[i].val;
 65             if(dis1[v] > dis1[u] + w){
 66                 dis1[v] = dis1[u] + w;
 67                 q.push(PII(dis1[v], v));
 68             } 
 69         }
 70     }
 71 }
 72 void dijk2(){
 73     while(!q.empty()) q.pop();
 74     memset(vis, 0, sizeof(vis));
 75     memset(dis2, 0x3f, sizeof(dis2));
 76     dis2[d] = 0;
 77     q.push(PII(0, d));
 78     while(!q.empty()){
 79         int u = q.top().second; q.pop();
 80         if(vis[u]) continue;
 81         vis[u] = 1;
 82         for(int i = head1[u]; i != -1; i = edges1[i].next){
 83             int v = edges1[i].to, w = edges1[i].val;
 84             if(dis2[v] > dis2[u] + w){
 85                 dis2[v] = dis2[u] + w;
 86                 q.push(PII(dis2[v], v));
 87             } 
 88         }
 89     }
 90 }
 91 void solve(){
 92     dijk1();
 93     dijk2();
 94     int mdis = dis1[d];
 95     if(mdis == inf) {
 96         puts("-1");
 97         return;
 98     }
 99     for(int i = 0; i < n; i++){
100         a[i].clear();
101         for(int j = head[i]; j != -1; j = edges[j].next){
102             int v = edges[j].to, w = edges[j].val;
103             int tp = dis1[i] + dis2[v] + w;
104             if(tp == mdis) a[i].insert(v);
105         }
106     }
107     dijk();
108     printf("%d\n", dis[d] == inf? -1: dis[d]);
109 }
110 int main(){
111     while(scanf("%d %d", &n, &m) && n != 0){
112         init();
113         scanf("%d %d", &s, &d);
114         for(int i = 0; i < m; i++){
115             int u, v, w;
116             scanf("%d %d %d", &u, &v, &w);
117             addEdge(u, v, w);
118             addEdge1(v, u, w);
119         }
120         solve();
121     }
122 }

题目：

SAMER08A - Almost Shortest Path

#graph-theory #shortest-path #dijkstra-s-algorithm

 

Finding the shortest path that goes from a starting point to a destination point given a set of points and route lengths connecting them is an already well known problem, and it's even part of our daily lives, as shortest path programs are widely available nowadays.

Most people usually like very much these applications as they make their lives easier. Well, maybe not that much easier.

Now that almost everyone can have access to GPS navigation devices able to calculate shortest paths, most routes that form the shortest path are getting slower because of heavy traffic. As most people try to follow the same path, it's not worth it anymore to follow these directions.

With this in his mind, your boss asks you to develop a new application that only he will have access to, thus saving him time whenever he has a meeting or any urgent event. He asks you that the program must answer not the shortest path, but the almost shortest path. He defines the almost shortest path as the shortest path that goes from a starting point to a destination point such that no route between two consecutive points belongs to any shortest path from the starting point to the destination.

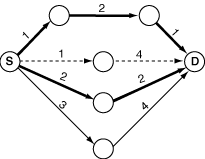
For example, suppose the figure below represents the map given, with circles representing location points, and lines representing direct, one-way routes with lengths indicated. The starting point is marked as S and the destination point is marked as D. The bold lines belong to a shortest path (in this case there are two shortest paths, each with total length 4). Thus, the almost shortest path would be the one indicated by dashed lines (total length 5), as no route between two consecutive points belongs to any shortest path. Notice that there could exist more than one possible answer, for instance if the route with length 3 had length 1. There could exist no possible answer as well.

subir imagenes

Input

The input contains several test cases. The first line of a test case contains two integers N (2 ≤ N ≤ 500) and M (1 ≤ M≤ 104), separated by a single space, indicating respectively the number of points in the map and the number of existing one-way routes connecting two points directly. Each point is identified by an integer between 0 and N -1. The second line contains two integers S and D, separated by a single space, indicating respectively the starting and the destination points (S ≠ D; 0 ≤ S, D < N). 

Each one of the following M lines contains three integers U, V and P (U ≠ V; 0 ≤ U, V < N; 1 ≤ P ≤ 103), separated by single spaces, indicating the existence of a one-way route from U to V with distance P. There is at most one route from a given point U to a given point V, but notice that the existence of a route from U to V does not imply there is a route from V to U, and, if such road exists, it can have a different length. The end of input is indicated by a line containing only two zeros separated by a single space.

Output

For each test case in the input, your program must print a single line, containing -1 if it is not possible to match the requirements, or an integer representing the length of the almost shortest path found. 

Example

Input:
7 9
0 6
0 1 1
0 2 1
0 3 2
0 4 3
1 5 2
2 6 4
3 6 2
4 6 4
5 6 1
4 6
0 2
0 1 1
1 2 1
1 3 1
3 2 1
2 0 3
3 0 2
6 8
0 1
0 1 1
0 2 2
0 3 3
2 5 3
3 4 2
4 1 1
5 1 1
3 0 1
0 0


Output:
5
-1
6
posted @ 2017-09-06 16:13  EricJeffrey  阅读(506)  评论(0)  编辑  收藏  举报