CF Round 431 C. From Y to Y
题目链接:http://codeforces.com/contest/849/problem/C
题目大意:给出一个数字K,现在要求构造一个只包含小写字母的可重集合使得集合的最小值为K。一个集合的值定义为:将所有字母看作长度为1的字符串,每次从中取出两个字符串s,t,连接后将新串st加入原集合,s,t从中删除,这个过程花费为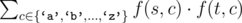 ,最后直到整个集合只包含一个字符串,那么总的花费值为每个过程花费值的累加和。
,最后直到整个集合只包含一个字符串,那么总的花费值为每个过程花费值的累加和。
解题思路:构造一个字符串使其最优累计值为K,那么首先会想,关键在于如何计算最有累计值,但是我们如果将整个过程反过来看,即将一个长度为N的字符串S拆成N个字母的字符集,那么我们可以每次从S中取出一个字母,认为他是最后加入到S中的,之后再从中取出一个……这样,对于K=5,我们构造一个长度x满足x*(x - 1) / 2 <= k的最大x的字符序列a,然后将k减去x * (x - 1) / 2,重复同样的过程,但是每次的字母都不一样,知道k为0. 注意K为0的情况。
不过,这个方法虽然可行但是我无法证明,只是想到了这种解法,感觉是对的。
代码:
1 const int maxn = 1e6 + 5; 2 int k; 3 4 void solve(){ 5 if(k == 0){ 6 printf("a"); 7 } 8 int tmk = k, cnt = 0; 9 while(tmk > 0){ 10 int x = (sqrt(1.0 + 8 * tmk) + 1) / 2; 11 tmk -= x * (x - 1) / 2; 12 while(x--) printf("%c", 'a' + cnt); 13 cnt++; 14 } 15 puts(""); 16 } 17 int main(){ 18 scanf("%d", &k); 19 solve(); 20 }
题目:




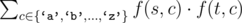 , where
, where 
