SPOJ FIBPOL - Fibonacci Polynomial

题目链接：http://www.spoj.com/problems/FIBPOL/

题目大意：F(n) 为斐波那契数列，现规定A(x) = Sn(Xⁿ*F(n)) ，即A(n)为数列Xⁿ*F(n)的前N项和，给定A(x)的值，问此时其对应X是否为一个有理数。

解题思路：首先我们可以计算出来一部分X对应的A(x)，可以发现，当X=0.5 或X = 0.6 时A(x)分别为2 15，都为整数。

https://projecteuler.net/problem=137 这是SPOJ本题下的一个评论中提到的相关题目，基本上是一样的，但是里面给出了第十个数是74049690，那么这个时候就可以OEIS了，然后。。。。打表就过了。

当然我们自然不会局限于那种方法，实际上是，A(X)是两个等比数列的前N项和的差。我们知道F(n)的通项公式：

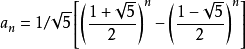
展开后再乘以Xⁿ 很明显就是两个等比数列前n项和的差。那么我们可以试着计算一下，会得到一个神奇的式子：

(X - F(n+1)Xⁿ⁺¹ - F(n)Xⁿ⁺²) / (1 - X - X²) = A(X). 

而分子的后面两项  F(n+1)Xⁿ⁺¹ - F(n)Xⁿ⁺² 在n趋近于无穷的时候已经为0，因此实际上变成了 A(X)  = X /  / (1 - X - X²)。然后将分母乘过去就会得到一个一元二次方程，那么我们就可以有求根公式反解出来X。

接下来就是看根号下的那个数是否是个完全平方数了。判断是否是完全平方数时要注意精度。

能够得到：

0:0
1:2
2:15
3:104
4:714
5:4895
6:33552
7:229970
8:1576239
9:10803704
10:42426697
11:74049690

然后与斐波那契数列比较就会发现，X = F(2 * n) * F(2 * n + 1)

代码：

const int inf = 0x3f3f3f3f;
const int maxn = 1e6 + 5;

bool solve(double x){
    double ans = sqrt(5.0 * x * x + 2.0 * x + 1.0);
    if(fabs(ans - (ll)ans) < 1e-8)
        return true;
    return false; 
}
int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        double x;
        scanf("%lf", &x);
        if(solve(x)) puts("1");
        else puts("0");
    }
}

题目：

FIBPOL - Fibonacci Polynomial

#math #number-theory

 

Let F(n) be the nth member of the Fibonacci sequence:

F(0) = 0, F(1) = 1,  
F(n) = F(n-1)+F(n-2) (n > 1)

Consider the following Fibonacci polynomial:

A(x) = x F(1) + x2 F(2) + x3 F(3) + ... + xn F(n) + ....
= sigma(n = 0 to infinity) xn F(n)

Amazingly,

A(1/2) = 1/2 + 1/22 + 2/23 + 3/24 + .... + F(n)/2n + ... = 2

In this problem, we only considering the non-negative-integer value of A(x). Here are some examples of A(x) for specific x.

x	A(x)
0	0
sqrt(2)-1	1
1/2	2
[sqrt(13)-2]/3	3
[sqrt(89)-5]/8	4

Find out if x is rational with the given value of A(x)

Input

The first line contains T, the number of test cases. The next T lines contains the value of A(x).

• 0 <= Ax <= 10^17
• 1 <= T <= 100000

Output

• 1 if the given Ax yeilds a rational x, 0 otherwise

Example

Input:
5

0

1

2

3

4

Output:
1

0

1

0

0