信道的定义与数学模型

1.信道的定义与分类：

定义：以传输媒介为基础的信号通道

狭义信道：根据传输媒介分为有线信道和无线信道。

　　有限信道：同轴电缆，光纤

　　无线信道：微波视距传播，卫星中继，移动通信信道等（比如：两个人之间的手机通信）

广义信道：根据研究问题分为调制信道，编码信道

　　调制信道：研究调制、解调问题 调制器输出-->解调器输入

　　编码信道：研究编码/译码问题 编码器输出-->译码器输入

 

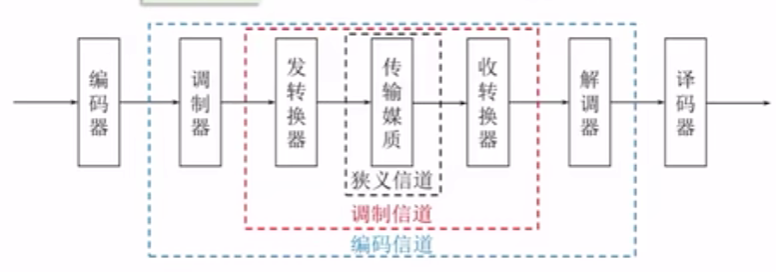
 广义信道的性能根本上还是取决于狭义信道

恒参信道与随参信道：

恒惨信道：信道传输特性随时间缓慢变化或不变化的信道

如：各种有线信道，卫星中继，超短波及微波视距传播，同轴电缆，对称电缆（双绞线），光纤

随参信道：信道传输特性随时间随机快速变化的信道。

如：短波电离层反射、各种散射、移动通信信道等...

调制信道数学模型：

1.有一对/多对输入/输出端；

2.大多满足线性叠加原理（即为线性网络）；

3.对信号有固定或时变的延迟和损耗；

4.无信号输入，仍有可能输出，此时输出噪声。

调制信道的数学模型：叠加有噪声的线性时变/时不变滤波器

 

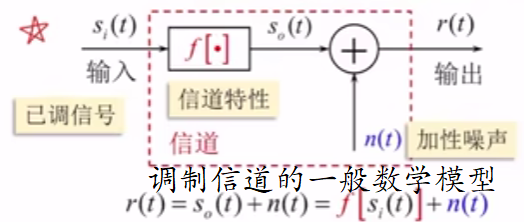
f[·] 就是滤波器 

1.恒参信道：对应的信道特性为线性时不变滤波器

也就是说这个信道对应的函数可以用一个冲击响应c(t)进行描述

c(t)的傅里叶变换是C（ω）

一般可以把c(t)叫做传输函数或者平均响应

 

对应的信道特性为线性时不变滤波器

 

 存在一种特殊的情形 如果：

C（ω）= K

C（ω）也叫做传输函数，假设传输函数为常数，信号频带内为常数（对应下图）

 

 

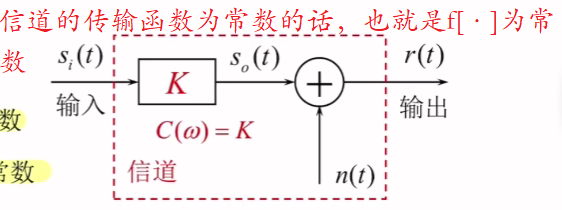
 这种情况的信道叫做加性高斯噪声信道

随参信道的特性：

对应的信道特性为线性时变滤波器

f[·] = c(t,τ)  c(t,τ)<=> C(ω,τ) 乘性干扰

这里τ表示的是时延差，所以此时的乘性干扰变成与ω和τ有关的参数

编码信道的数学模型

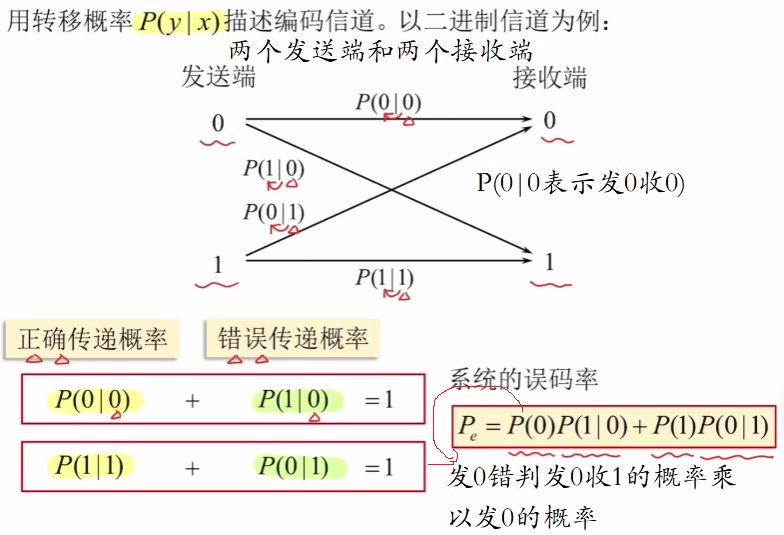
用转移概率P（y|x）描述编码信道。以二进制信道为例：

编码信道传输的是离散的码元，所以编码信道也是一种离散信道

 

 

 编码信道的分类：

1.无记忆信道：前后码元发生的错误相互独立

2.有记忆信道：一个码元发生的错误与前后码元有依赖关系，需要用马尔科夫链描述