opencv相机标定(Python)

相机标定

相机标定的目的

获取摄像机的内参和外参矩阵（同时也会得到每一幅标定图像的选择和平移矩阵），内参和外参系数可以对之后相机拍摄的图像就进行矫正，得到畸变相对很小的图像。

相机标定的输入

标定图像上所有内角点的图像坐标，标定板图像上所有内角点的空间三维坐标（一般情况下假定图像位于Z=0平面上）。

相机标定的输出

摄像机的内参、外参系数。

 

拍摄的物体都处于三维世界坐标系中，而相机拍摄时镜头看到的是三维相机坐标系，成像时三维相机坐标系向二维图像坐标系转换。不同的镜头成像时的转换矩阵不同，同时可能引入失真，标定的作用是近似地估算出转换矩阵和失真系数。为了估算，需要知道若干点的三维世界坐标系中的坐标和二维图像坐标系中的坐标，也就是拍摄棋盘的意义。

相机成像

相机的成像原理:小孔成像

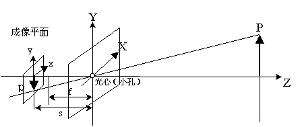
相机的内参

相机的外参

在实际由于设计工艺问题、相机安装环境或物体摆放位置等影响，会照成成像与实际图像不一样的现象。

由于设计工艺照成的影响是无法改变的事实，所以这将是相机的内参；

由环境或安装方式照成的影响是可以改变的，这就是相机的外参。

 

张正友标定相机原理

　　　　1.求得相机内参数：

　　　　　　用于标定的棋盘格是特制的，其角点坐标已知。标定棋盘格是三维场景中的一个平面∏，棋盘格在成像平面为π(知道了∏与π的对应点坐标之后，可求解两个平面1对应的单应矩阵H)。

　　　　　　根据相机成像模型，P为标定的棋盘坐标，p为其像素点坐标。则，通过对应的点坐标求解H后，可用于求K,R,T。

　　　　2.设棋盘格所在平面为世界坐标系上XOY平面，则棋盘格上任一角点P世界坐标系为(X,Y,0)。

　　　　

　　　　3、内参约束条件

　　　　　　

　　　　　　

　　　　　　

　　　　　　

 

 

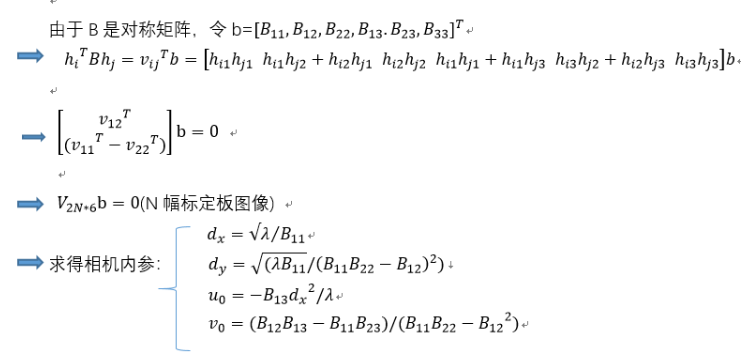
实验步骤

打印棋盘图片（网上找一张）

 

 

 将打印出的纸固定放到一个平面上，使用同一相机从不同的位置，不同的角度，拍摄标定板的多张照片（我拍了15张）手机型号是华为mate9

 

 

提取标定板的世界坐标

标定板的大小是标定板在水平和竖直方向上内角点的个数。内角点指的是，标定板上不挨着边界的角点。

我打印的是6x9的标定板。

 

 

标定相机

 

 

 

 

 

 

 

 

 

 

mtx -->内参数矩阵
dist --> 畸变系数
rvecs --> 旋转向量
tvecs --> 平移向量

我们可以通过反投影误差来评估结果的好坏，越接近0，说明结果越理想。

通过之前计算的内参数矩阵、畸变系数、旋转矩阵和平移向量，使用cv2.projectPoints()计算三维点到二维图像的投影，然后计算反投影得到的点与图像上检测到的点的误差，最后计算一个对于所有标定图像的平均误差即反投影误差

 我的棋盘打印出来有些不平整，可能是打印的纸张没有放正，导致有些地方翘着，效果不是很好，误差值有些大了，把纸张贴平整应该会好很多。而且我可能拍照的角度变化不是太大，可以试着把拍照的角度更加差异些，结果会更明显。 

 

 

import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)

# 获取标定板角点的位置
objp = np.zeros((6 * 9, 3), np.float32)
objp[:, :2] = np.mgrid[0:9, 0:6].T.reshape(-1, 2)  # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = []  # 存储3D点
img_points = []  # 存储2D点

images = glob.glob("E:/test_pic/qipan/*.jpg")
for fname in images:
    img = cv2.imread(fname)

    cv2.imshow('img',img)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

    size = gray.shape[::-1]
    ret, corners = cv2.findChessboardCorners(gray, (6, 9), None)

    print(ret)

    if ret:

        obj_points.append(objp)

        corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
        #print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)

        cv2.drawChessboardCorners(img, (8, 6), corners, ret)  # 记住，OpenCV的绘制函数一般无返回值

        cv2.imshow('img', img)
        cv2.waitKey(2000)

print(len(img_points))
cv2.destroyAllWindows()

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print("ret:", ret)
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs)  # 旋转向量  # 外参数
print("tvecs:\n", tvecs ) # 平移向量  # 外参数

print("-----------------------------------------------------")