蚁群算法

　　　　　　　　　　　　　　　　　  蚁群算法

蚁群算法是一种用来寻找优化路径的概率型算法。它由Marco Dorigo于1992年提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。这种算法具有分布计算、信息正反馈和启发式搜索的特征，本质上是进化算法中的一种启发式全局优化算法。

 

蚁群算法的基本原理

1、蚂蚁在路径上释放信息素。

2、碰到还没走过的路口，就随机挑选一条路走。同时，释放与路径长度有关的信息素。

3、信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时，就选择信息素浓度较高路径。

4、最优路径上的信息素浓度越来越大。

5、最终蚁群找到最优寻食路径。

 

 

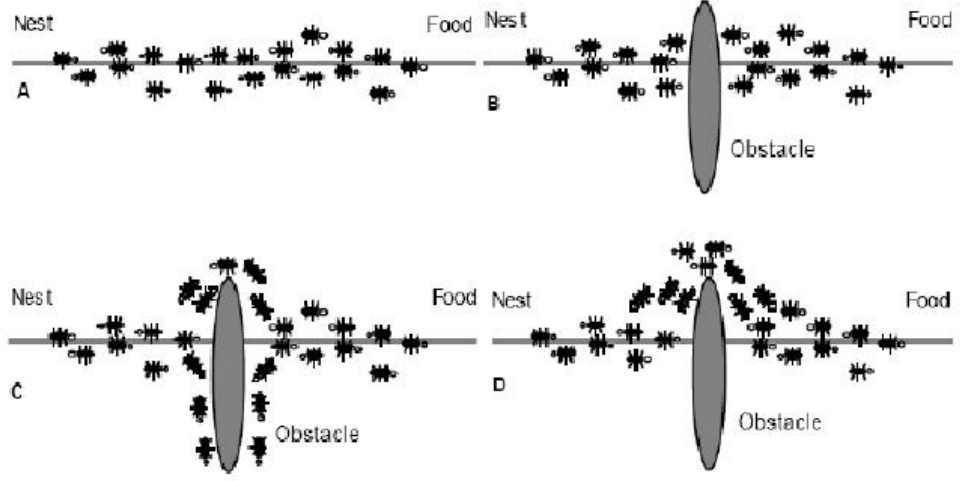
 蚁群走过较短的那一侧的蚂蚁数数量会多于较长那一侧的，所以留下的信息素就会多，渐渐的蚂蚁就只走较短的那一侧了。

 

蚁群算法对TSP的求解主要有两大步骤：（TSP问题就是要找到最短哈密尔顿回路）

1、路径构建

AS中的随机比例规则；对于每只蚂蚁k，路径记忆向量R^k.按照访问顺序记录了所有k已经经过的城市序号。设蚂蚁k当前所在城市为i,则其选择城市j作为下一个访问对象的概率为:

 

 

2、信息素更新

 

这里m是蚂蚁个数, ρ是信息素的蒸发率，规定0≤ ρ≤1，在AS中通常设置为 ρ =0.5，Δτij是第k只蚂蚁在它经过的边上释放的信息素量，它等于蚂蚁k本轮构建路径长度的倒数。C^k表示路径长度，它是R^k中所有边的长度和。

构建图：构建图与问题描述图是一致的，成份的集合C对应着点的集合（即：C=N），连接对应着边的集合（即L=A）,且每一条边都带有一个权值，代表点i和j之间的距离。

约束条件：所有城市都要被访问且每个城市最多只能被访问一次。

信息素和启发式信息：TSP 问题中的信息素表示在访问城市i后直接访问城市j的期望度。启发式信息值一般与城市i和城市j的距离成反比。

解的构建：每只蚂蚁最初都从随机选择出来的城市出发，每经过一次迭代蚂蚁就向解中添加一个还没有访问过的城市。当所有城市都被蚂蚁访问过之后，解的构建就终止。

 

 

 

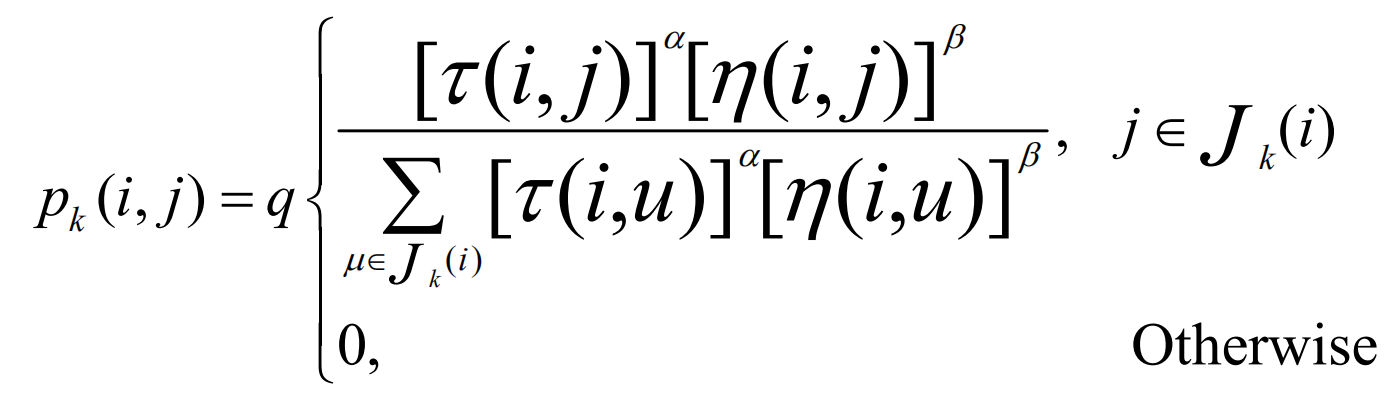
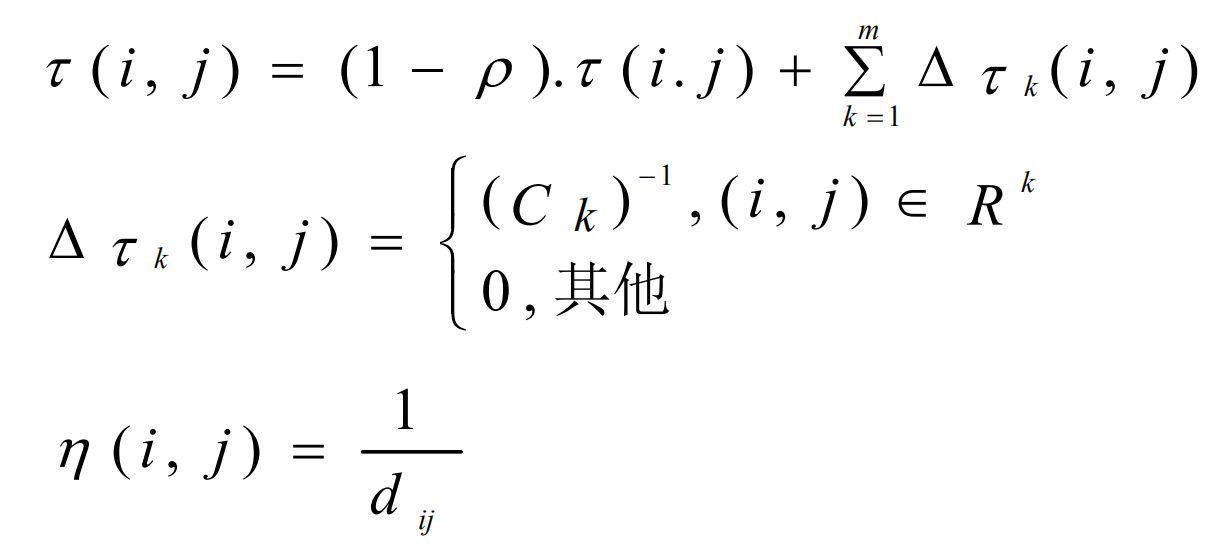
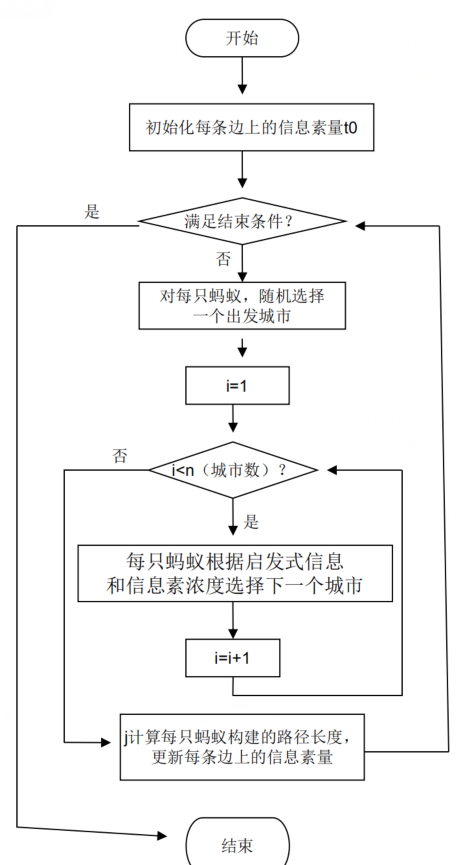
蚁群算法存在缺陷：

蚁群算法在解决小规模TSP问题是勉强能用，稍加时间就能发现最优解，但是若问题规模很大，蚁群算法的性能会极低，甚至卡死。所以可以进行改进，例如精英蚂蚁系统。

精英蚂蚁系统是对基础蚁群算法的一次改进，它在原AS信息素更新原则的基础上增加了一个对至今最优路径的强化手段。在每轮信息素更新完毕后，搜索到至今最优路径的那只蚂蚁将会为这条路径添加额外的信息素。精英蚂蚁系统引入 这种额外的信息素强化手段有助于更好的引导蚂蚁搜索的偏向，使算法更快收敛

 

 

 

 

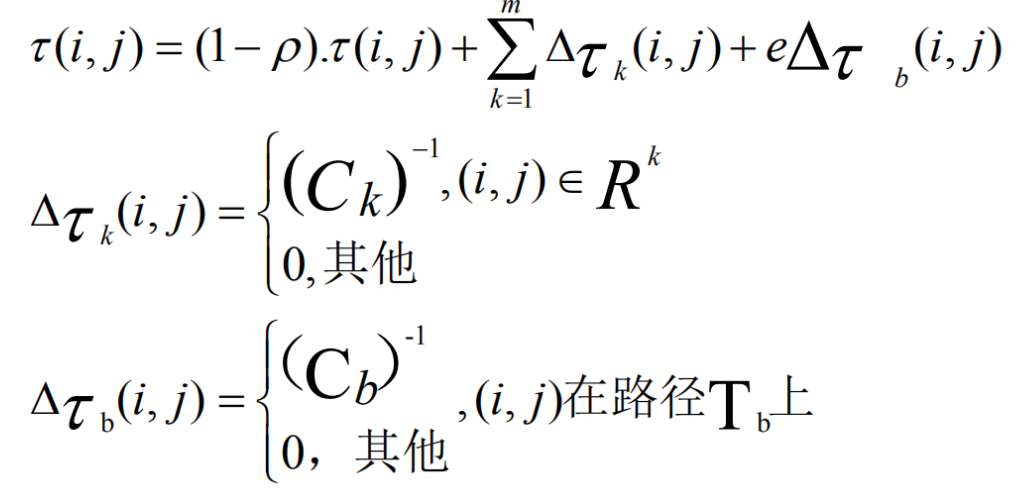
针对不同影响因素进行测试

m = 50; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子

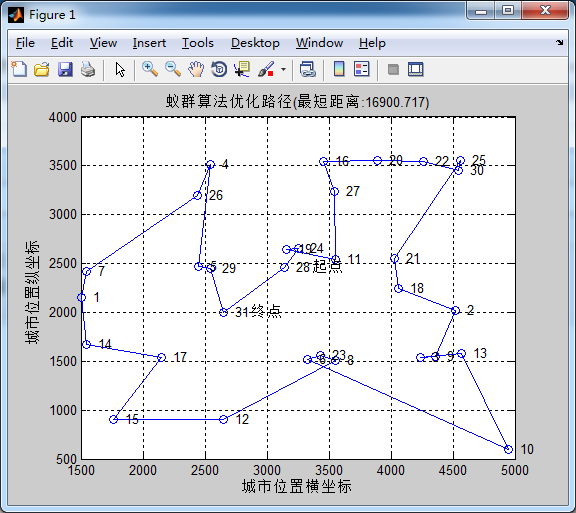
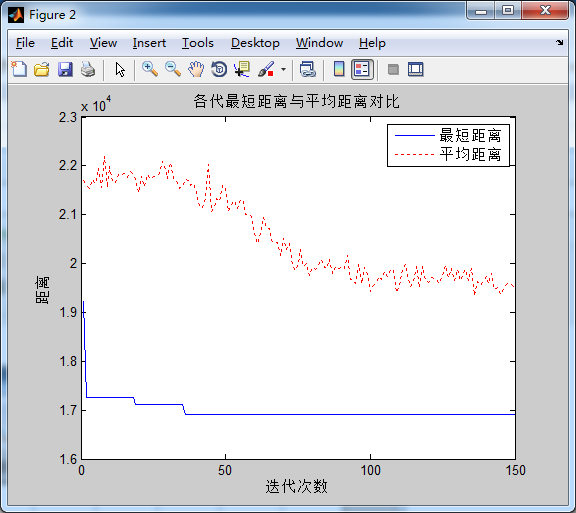
蚂蚁数量50，信息素重要程度因子1，启发函数重要程度因子5， 信息素挥发因子0.1在迭代次数在40次左右收束

 

 

m = 50; % 蚂蚁数量
alpha = 0.5; % 信息素重要程度因子
beta = 10; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子

 

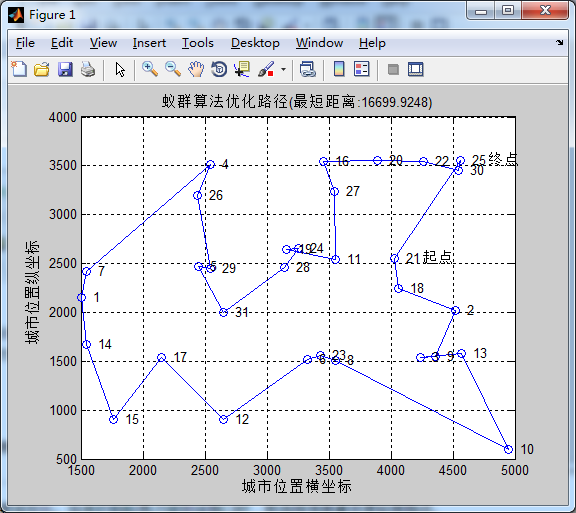
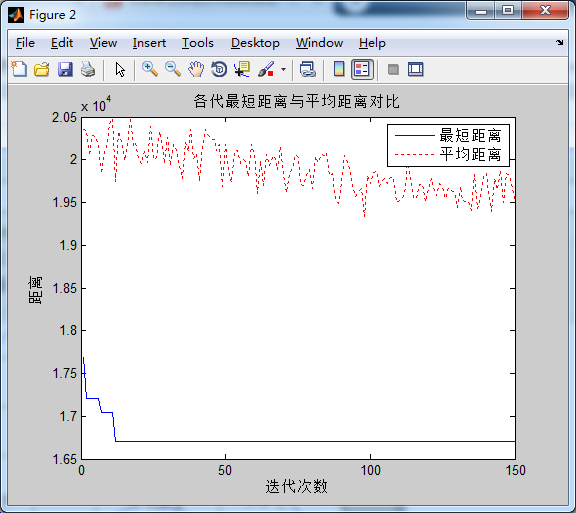
蚂蚁数量50，信息素重要程度因子0.5，启发函数重要程度因子10， 信息素挥发因子0.1在迭代次数在15次左右收束 ，大幅减少迭代次数（降低了信息素，增加了启发函数重要程度因子）

 

 

m = 50; % 蚂蚁数量
alpha = 0.1; % 信息素重要程度因子
beta = 10; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子

 

 

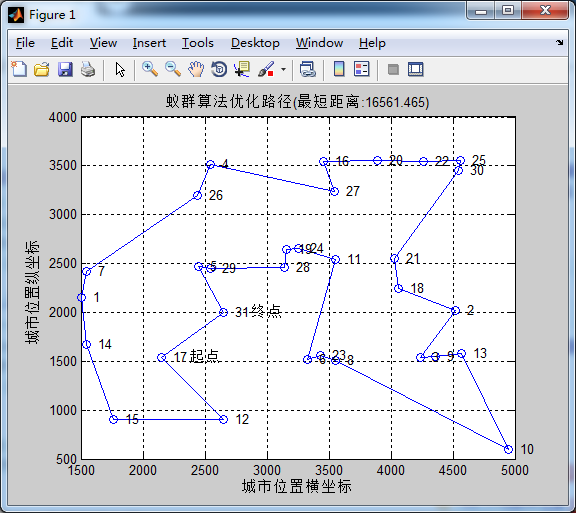
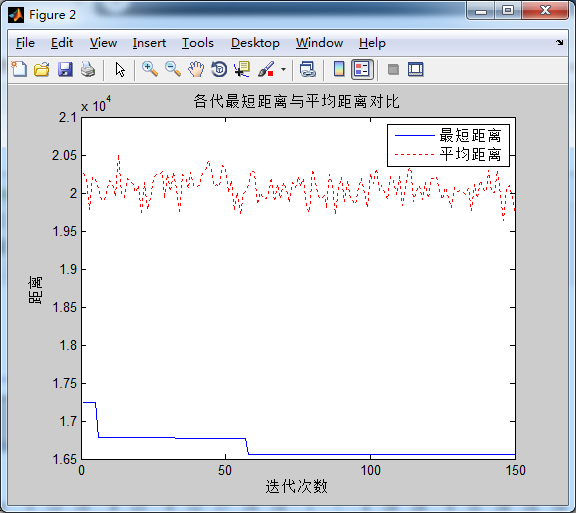
蚂蚁数量50，信息素重要程度因子0.1，启发函数重要程度因子10， 信息素挥发因子0.1在迭代次数在60次左右收束 ，迭代次数不减反增，可见信息素重要程度因子不能过小

 

m = 50; % 蚂蚁数量
alpha = 0.1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子

 

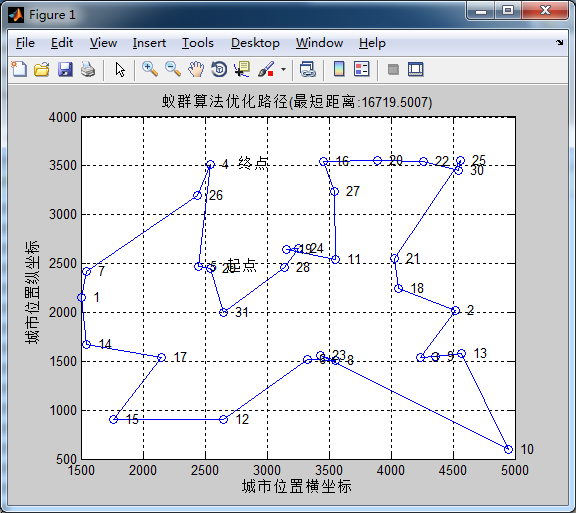
蚂蚁数量50，信息素重要程度因子0.1，启发函数重要程度因子5， 信息素挥发因子0.1在迭代次数在55次左右收束，启发函数重要程度因子在超过一定数值后并不能有效降低，所以启发函数重要程度因子不宜超过5

 

m = 100; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子

 

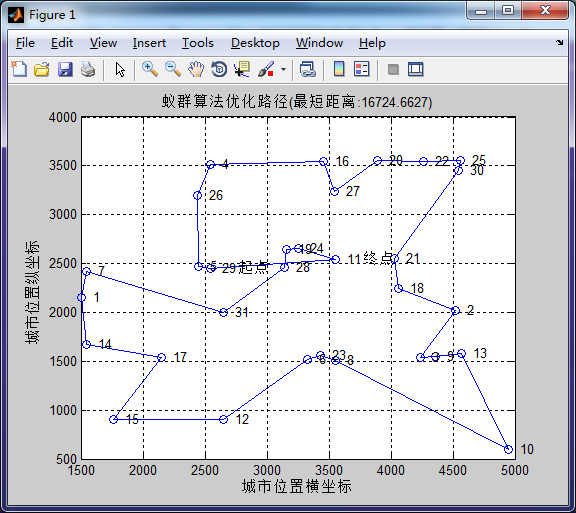
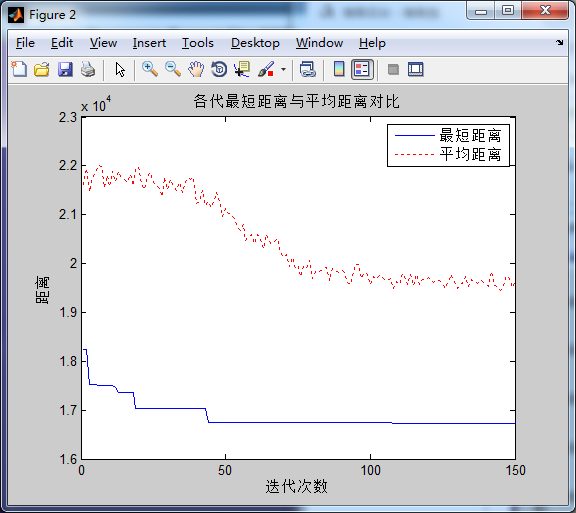
 蚂蚁数量100，信息素重要程度因子1，启发函数重要程度因子5， 信息素挥发因子0.1在迭代次数在45次左右收束，增加蚁群数量后能一定程度上减少迭代次数，但是没有明显作用，且增加了运行时间成本，不建议过大。

 

m = 50; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.2; % 信息素挥发因子

 

 

 

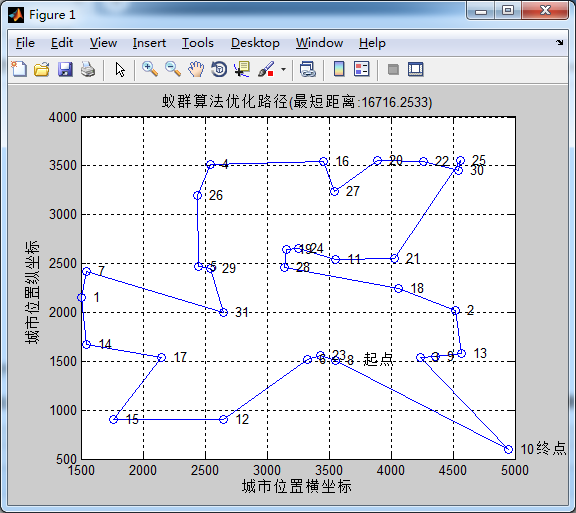
 蚂蚁数量50，信息素重要程度因子1，启发函数重要程度因子5， 信息素挥发因子0.2在迭代次数在60次左右收束，信息素挥发因子在增大也没有更加明显的优化了，推荐0.1-0.2即可。

 

 蚁群算法代码

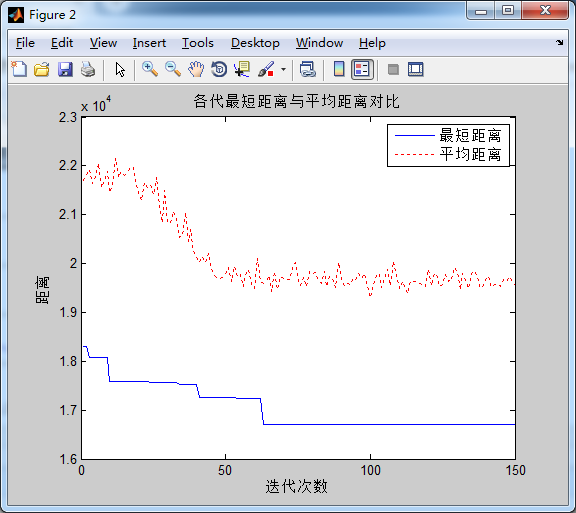
%% 旅行商问题(TSP)优化
%% 清空环境变量
clear all
clc

%% 导入数据
load citys_data.mat

%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;      
        end
    end    
end

%% 初始化参数
fprintf('Initializing Parameters... \n');
m = 50;                              % 蚂蚁数量
alpha = 1;                           % 信息素重要程度因子
beta = 5;                            % 启发函数重要程度因子
rho = 0.2;                           % 信息素挥发因子
Q = 1;                               % 常系数
Eta = 1./D;                          % 启发函数
Tau = ones(n,n);                     % 信息素矩阵
Table = zeros(m,n);                  % 路径记录表
iter = 1;                            % 迭代次数初值
iter_max = 150;                      % 最大迭代次数 
Route_best = zeros(iter_max,n);      % 各代最佳路径       
Length_best = zeros(iter_max,1);     % 各代最佳路径的长度  
Length_ave = zeros(iter_max,1);      % 各代路径的平均长度  

%% 迭代寻找最佳路径
figure;
while iter <= iter_max
    fprintf('迭代第%d次\n',iter);
    % 随机产生各个蚂蚁的起点城市
      start = zeros(m,1);
      for i = 1:m
          temp = randperm(n);
          start(i) = temp(1);
      end
      Table(:,1) = start; 
      % 构建解空间
      citys_index = 1:n;
      % 逐个蚂蚁路径选择
      for i = 1:m
          % 逐个城市路径选择
         for j = 2:n
             tabu = Table(i,1:(j - 1));           % 已访问的城市集合(禁忌表)
             allow_index = ~ismember(citys_index,tabu);
             allow = citys_index(allow_index);  % 待访问的城市集合
             P = allow;
             % 计算城市间转移概率
             for k = 1:length(allow)
                 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
             end
             P = P/sum(P);
             % 轮盘赌法选择下一个访问城市
             Pc = cumsum(P);     
            target_index = find(Pc >= rand); 
            target = allow(target_index(1));
            Table(i,j) = target;
         end
      end
      % 计算各个蚂蚁的路径距离
      Length = zeros(m,1);
      for i = 1:m
          Route = Table(i,:);
          for j = 1:(n - 1)
              Length(i) = Length(i) + D(Route(j),Route(j + 1));
          end
          Length(i) = Length(i) + D(Route(n),Route(1));
      end
      % 计算最短路径距离及平均距离
      if iter == 1
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;  
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - 1),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
          else
              Route_best(iter,:) = Route_best((iter-1),:);
          end
      end
      % 更新信息素
      Delta_Tau = zeros(n,n);
      % 逐个蚂蚁计算
      for i = 1:m
          % 逐个城市计算
          for j = 1:(n - 1)
              Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
          end
          Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
      end
      Tau = (1-rho) * Tau + Delta_Tau;
    % 迭代次数加1，清空路径记录表

 %   figure;
 %最佳路径的迭代变化过程
    [Shortest_Length,index] = min(Length_best(1:iter));
    Shortest_Route = Route_best(index,:);
    plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
    [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
    pause(0.3);
 
    iter = iter + 1;
    Table = zeros(m,n);

 % end
end

%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);

%% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
     [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
    text(citys(i,1),citys(i,2),['   ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),'       起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),'       终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')

 

 

 

 总结

蚁群算法(AS)的缺点：

1、收敛速度慢（运行一次要等好久）

2、易于陷入局部最优

 

m -> 蚂蚁数量:

m数目越多,得到的最优解就越精确,但是会有蚂蚁重复路过同一城市,大量的重复增加了运行时间（100差不多了，运行好久）

 

alpha -> 信息素重要程度因子:

alpha值过大,蚂蚁选择之前走过的路径可能性就越大,蚁群搜索路径的随机性减弱。alpha值过小,蚁群搜索范围就会减少,易陷入局部最优解。（感觉1或者2就挺好）

beta -> 启发函数重要程度因子：

beta值增大,蚁群更容易选择局部较短路径,能加快算法的运行速度,但是可能陷入局部最优解（4或5就挺大的了）

 

rho -> 信息素挥发因子：

rho值初始设置为0.1，当rho很小的时候，每条路径的残留信息很多，会被反复搜索，增加运行时间。rho设置的很大的时候,会放弃搜索很多有效路径,可能会忽略最优值。