GNSS定位_粒子滤波
结论
1. 在相同的运动模型下,PF的粒子数量越多,定位精度越高
2. 系统运动不确定度越大,即越随机,对应的驱动噪声亦应设置越大,才能通过运动模型预测去覆盖可能达到的状态点,否则系统可能无法收敛到最优解,逐渐发散
3. 在相同的粒子数量下,系统越随机,则定位精度越低
4. 在粒子数量一定的情况下,通过重采样,尽可能多的保留有效的粒子,提升估计精度,但是会损失一定的多样性,尤其是在系统非线性比较严重或者运动随机性比较大的场景,会由于损失了粒子的多样性而损失一定的精度,甚至发散。
5. PF的关键在于粒子,既保证粒子的有效数量,又能保证粒子的多样性,这样才能确保系统稳定而又准确的估计所需的状态
实现
python实现如下:
1 #!/usr/bin/env python 2 # -*- encoding: utf-8 -*- 3 ''' 4 @File : pvt_pf.py 5 @Time : 2022/08/18 11:39:26 6 @Author : qfr 7 @Version : 1.0 8 @Contact : qfr@whu.edu.cn 9 @License : (C)Copyright 2021-2025, qfr&lz 10 @Desc : pvt particle filter simulation 11 ''' 12 13 # here put the import lib 14 import numpy as np 15 from cmath import * 16 # import local lib 17 import global_cfg as ct 18 19 class PvtPf(object): 20 def __init__(self, meas, sat, ls, ts): 21 self.__meas = meas # 引用meas信息的地址 22 self.__sat = sat # 引用sat信息的地址 23 self.__ls = ls # 引用最小二乘信息的地址 24 25 self.__ts = ts 26 self.__init = False 27 28 # PF 参数 29 self.__NP = 1000 # Number of Particle 30 self.__NTh = self.__NP / 2.0 # Number of particle for re-sampling 31 32 def __PfInit(self): 33 self.__x = np.hstack((self.__ls.pos, self.__ls.vel, self.__ls.clkBias, self.__ls.clkDrift)) 34 self.__px = np.zeros((self.__NP, 1)) + self.__x.reshape((1, len(self.__x))) 35 self.__wx = np.zeros((self.__NP, )) + 1 / self.__NP 36 37 # 系统驱动噪声设置 38 # (系统噪声数量为5,包含三维的运动驱动噪声和 两维的时钟驱动噪声) 39 h0 = 2e-18 40 h_2 = 2e-20 41 42 st = h0 / 2.0 * ct.C**2 43 sf = 2. * pow(np.pi, 2) * h_2 * ct.C**2 # 对应时钟噪声的方差 44 svx = 0.5 45 svy = 0.5 46 svz = 0.1 # 对应运动噪声的方差 47 self.__noisePara = np.hstack((svx, svy, svz, st, sf)) 48 49 def __GaussLikelihood(self, x, sigma): 50 p = 1.0 / np.sqrt(2.0 * np.pi * sigma ** 2) * \ 51 np.exp(-x ** 2 / (2 * sigma ** 2)) 52 return p 53 54 def __PfPredict(self, i): 55 # 噪声生成 56 noise = np.random.randn(len(self.__noisePara)) 57 noise = np.sqrt(self.__noisePara) * noise 58 59 # 状态更新(离散化) 60 # 噪声驱动更新(确保在符合运动模型的情况下尽可能保证粒子的多样性) 61 # 可通过调整运动模型参数(驱动噪声大小) 来确保粒子能覆盖所有可能的状态点信息 62 tmp1 = self.__ts **2 / 2. 63 tmp2 = self.__ts **3 / 3. 64 self.__px[i, :3] += self.__ts * self.__px[i, 3:6] + tmp2 * noise[:3] 65 self.__px[i, 3:6] += self.__ts * noise[:3] 66 self.__px[i, -2] += self.__ts * self.__px[i, -1] + tmp2 * noise[-1] + self.__ts * noise[-2] 67 self.__px[i, -1] += self.__ts * noise[-1] 68 69 def __Resampling(self, px, pw): 70 """ 71 low variance re-sampling 72 """ 73 74 w_cum = np.cumsum(pw) 75 base = np.arange(0.0, 1.0, 1 / self.__NP) 76 re_sample_id = base + np.random.uniform(0, 1 / self.__NP) 77 indexes = [] 78 ind = 0 79 for ip in range(self.__NP): 80 while re_sample_id[ip] > w_cum[ind]: 81 ind += 1 82 indexes.append(ind) 83 84 px = px[indexes] 85 pw = np.zeros((self.__NP, )) + 1 / self.__NP # init weight 86 return px, pw 87 88 def __PfUpdate(self): 89 # 遍历各个粒子,进行状态预测,并根据量测更新权重 90 for m in range(self.__NP): 91 # 根据运动模型进行预测 92 self.__PfPredict(m) 93 94 # 在最新预测的基础上进行量测更新 95 for i in range(self.__meas.measCount): # 遍历量测 96 if self.__meas.measPraim[i]: 97 continue 98 99 tmp1 = self.__px[m, :3] - self.__sat.pos[i] 100 tmp2 = np.sqrt(np.sum(np.square(tmp1))) 101 los = tmp1 / tmp2 102 103 dz = self.__meas.measP[i] - tmp2 - self.__px[m, -2] 104 self.__wx[m] *= self.__GaussLikelihood(dz, self.__meas.stdP[i]) 105 106 107 dz = self.__meas.measD[i] - np.dot(los, self.__px[m, 3:6]) - self.__px[m, -1] 108 #self.__wx[m] *= self.__GaussLikelihood(dz, self.__meas.stdD[i]) 109 110 # 权重归一化 111 self.__wx = self.__wx / self.__wx.sum() # normalize 112 113 # 获取最终估计的结果 114 self.__x = self.__px.transpose() @ self.__wx 115 116 # 重采样 117 N_eff = 1.0 / (self.__wx.dot(self.__wx)) # Effective particle number 118 if N_eff < self.__NTh: 119 self.__px, self.__wx = self.__Resampling(self.__px, self.__wx) 120 121 122 def Update(self): 123 124 if self.__init == False : 125 if self.__ls.posValid: 126 self.__PfInit() # kf初始化 127 self.__init = True 128 return False 129 130 self.__PfUpdate() 131 132 self.pos = self.__x[0:3] 133 self.vel = self.__x[3:6] 134 self.clkBias = self.__x[-2] 135 self.clkDrift = self.__x[-1] 136 137 return True
当N=1000定位结果如下:
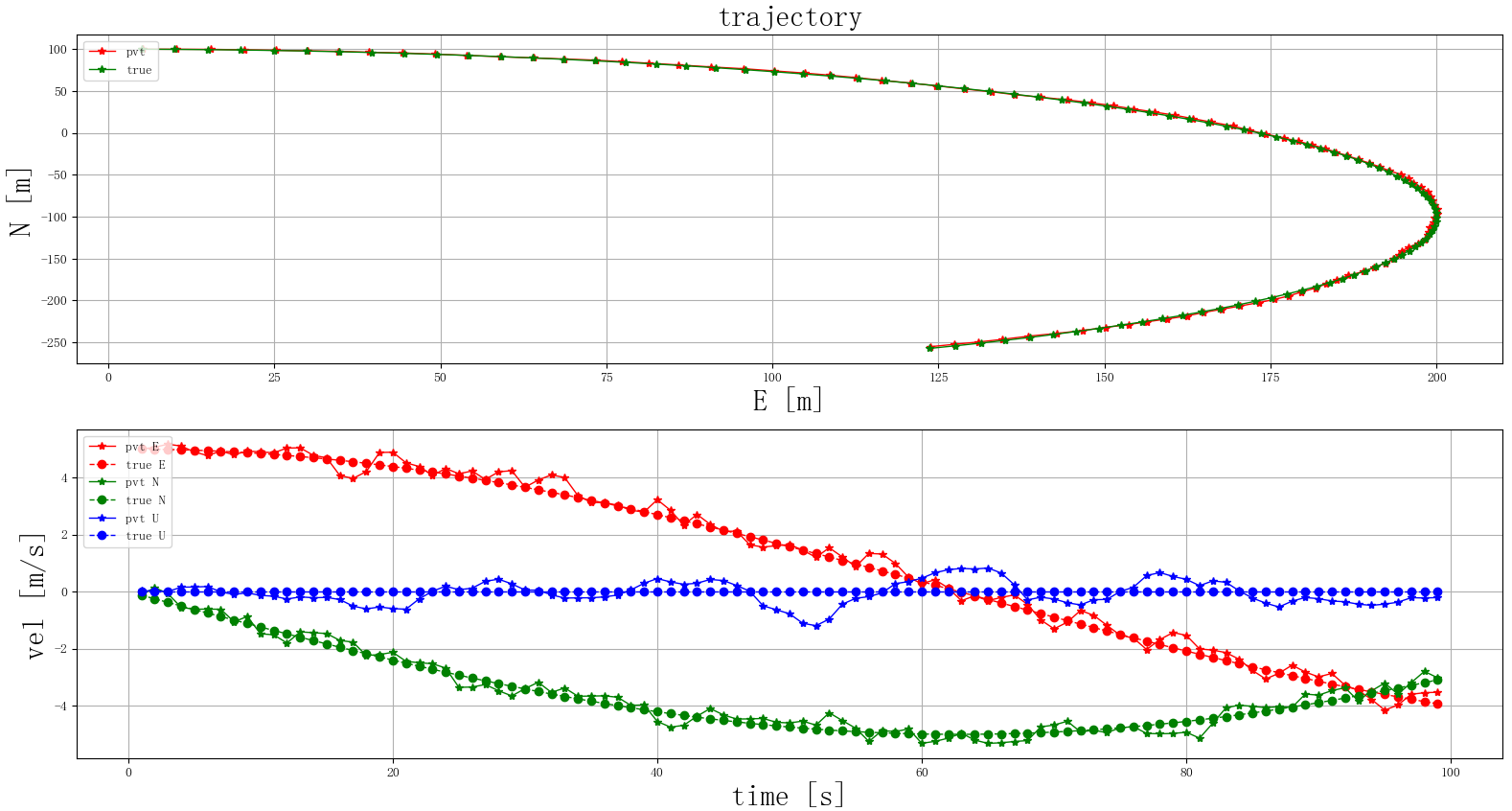
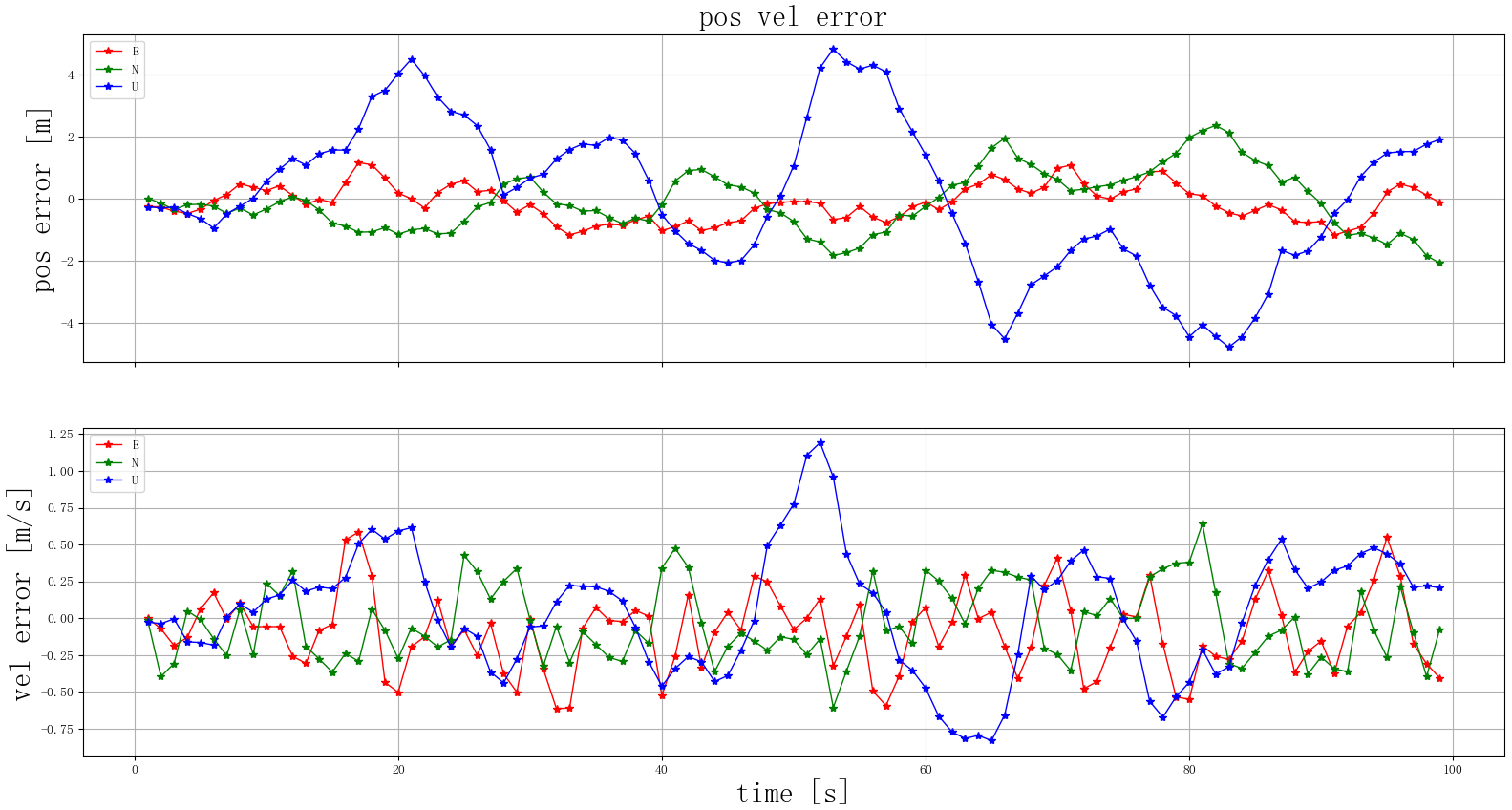
当N=50定位结果如下:
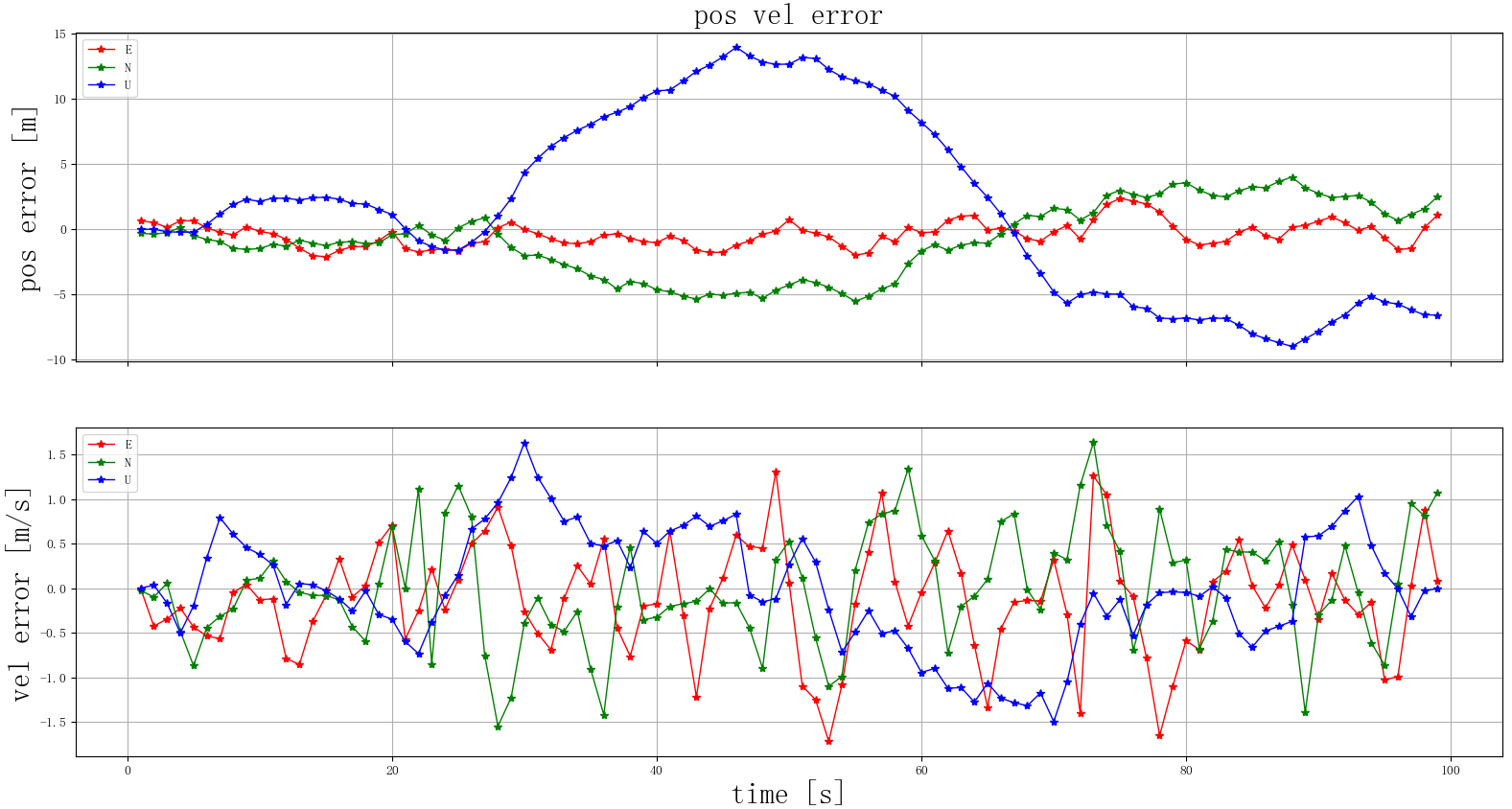
参考链接
Particle Filter Tutorial 粒子滤波:从推导到应用(一)
Particle Filter Tutorial 粒子滤波:从推导到应用(二)
Particle Filter Tutorial 粒子滤波:从推导到应用(三)
Particle Filter Tutorial 粒子滤波:从推导到应用(四) # 粒子滤波的详细推导及应用
LDA-math-MCMC 和 Gibbs Sampling # 随机模拟技术,蒙特卡洛技术详解
记录每天生活的点点滴滴,呵呵呵呵呵呵



