视觉SLAM 十四讲——3D-2D:PnP求解——BA

　　PnP问题的求解方法有很多，例如，用3对点估计位姿的P3P、直接线性变换法（DLT），EPnP(Efficient PnP)，UPnP等；

　　非线性优化的方式，构建最小二乘问题并迭代进行求解，即万金油式的Bundle Adjustment。

　　本节组要介绍BA，并给出示例。

主要内容

1. 概念

　　线性方法：先求解相机位姿，再求空间点位置

　　非线性优化方法：把相机位姿和空间点位置都看成优化变量，两者一起优化，通用的求解方式（PnP,ICP问题）。

　　在PnP问题中，Bundle Adjustment 问题是一个最小化重投影误差(Reprojection Error)的问题。

2. BA求解 (P163-165)

　　1）重投影误差公式表示

　　　　其中，为第i个特征点的像素坐标，为特征位置坐标。

　　2）线性化

　　　　求解每个误差项关于优化变量的导数：

　　　　其中，

　　　　　　优化变量为：李代数se(3)的扰动量，特征点的空间位置P

　　　　　　量测输入为：像素坐标点

　　　　2.1) 误差变化量对位姿扰动量的导数（2×6的雅克比矩阵）：

　　　　　　其中，需要注意：

　　　　　　a) 观测值-预测值，保留一阶导数前面的负号，　　

　　　　　　　　预测值-观测值，去掉负号。

　　　　　　b) 雅克比矩阵对应的se(3)中：平移在前，旋转在后，

　　　　　　　　如果旋转在前，平移在后，需要将矩阵的前三列与后三列对调。

　　　　2.2）误差变化量对特征点位置的导数（2×3的雅克比矩阵）：

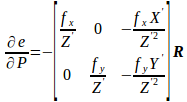
　　　　　　　　注：矩阵前面的负号，关系到残差的方向。

3. 应用

　　BA是一种通用的做法，可以不限于两幅图像，可以放入多幅图像的位姿和特征点进行优化，甚至可以把整个SLAM放进来。

　　当然，规模先对比较大，主要在后端使用。

　　在前段，主要考虑局部相机位姿和特征点的小型BA问题，希望对他进行实时求解和优化。

4. 代码注意的点

　　1） VertexSE3Expmap 顶点的定义：
　　　　模板参数： 6维的李代数，优化变量的类型为：SE3Quat（类的内部使用了四元数加位移向量来存储位姿，但同时也支持李代数上的运算）

　　　　位姿定点的增量更新实现函数：oplusImpl （其中实现了李代数的指数映射）

/**
 * \brief SE3 Vertex parameterized internally with a transformation matrix
 and externally with its exponential map
 */
class G2O_TYPES_SBA_API VertexSE3Expmap : public BaseVertex<6, SE3Quat>{　　
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW

  VertexSE3Expmap();

  bool read(std::istream& is);

  bool write(std::ostream& os) const;

  virtual void setToOriginImpl() {
    _estimate = SE3Quat();
  }

  virtual void oplusImpl(const double* update_)  {
    Eigen::Map<const Vector6d> update(update_);
    setEstimate(SE3Quat::exp(update)*estimate());
  }
};

　　2）VertexSBAPointXYZ 顶点的定义

　　　　模板参数：3维的向量表示特征点的位置，类型为Vector3D

　　　　特征点位置顶点的更新函数：增量相加

 class G2O_TYPES_SBA_API VertexSBAPointXYZ : public BaseVertex<3, Vector3D>
{
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW    
    VertexSBAPointXYZ();
    virtual bool read(std::istream& is);
    virtual bool write(std::ostream& os) const;

    virtual void setToOriginImpl() {
      _estimate.fill(0.);
    }

    virtual void oplusImpl(const double* update)
    {
      Eigen::Map<const Vector3D> v(update);
      _estimate += v;
    }
};

　　3） EdgeProjectXYZ2UV 边的定义：

　　　　3.1）模板参数定义：2维的量测信息，Vector2D，两个顶点类型 VertexSBAPointXYZ 以及 VertexSE3Expmap；

　　　　3.2）残差计算函数 computeError：

　　　　　　　先从该边连接的两个顶点中获取当前的位姿和特征点位置信息（更新到最近一次的信息）；

　　　　　　　其次，获取该边连接的参数信息，即相机的内参信息；

　　　　　　　最后，根据量测输入计算残差信息（map：将特征点位置根据当前位姿转化到相机坐标系；cam_map：将相机坐标系的点（归一化）通过内参K转化到像素坐标点）

　　　　3.3）投影方程的误差计算（量测方程线性化）：linearizeOplus的实现

class G2O_TYPES_SBA_API EdgeProjectXYZ2UV : public  BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>{
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    EdgeProjectXYZ2UV();

    bool read(std::istream& is);

    bool write(std::ostream& os) const;

    void computeError()  {
      const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
      const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);
      const CameraParameters * cam
        = static_cast<const CameraParameters *>(parameter(0));
      Vector2D obs(_measurement);
      _error = obs-cam->cam_map(v1->estimate().map(v2->estimate()));
    }

    virtual void linearizeOplus();

    CameraParameters * _cam;
};

　　4）量测方程线性化（分别对位姿和特征点位置求导）：linearizeOplus

　　　　4.1）特征点位置的求导结果：_jacobianOplusXi

　　　　 4.2）位姿的求导结果：_jacobianOplusXj （与上面的公式稍有差别，李代数中定义旋转在前）

　　　　 4.3）g2o的相机里，用f 统一描述 fx 和 fy。

void EdgeProjectXYZ2UV::linearizeOplus() {
  VertexSE3Expmap * vj = static_cast<VertexSE3Expmap *>(_vertices[1]);
  SE3Quat T(vj->estimate());
  VertexSBAPointXYZ* vi = static_cast<VertexSBAPointXYZ*>(_vertices[0]);
  Vector3D xyz = vi->estimate();
  Vector3D xyz_trans = T.map(xyz);

  double x = xyz_trans[0];
  double y = xyz_trans[1];
  double z = xyz_trans[2];
  double z_2 = z*z;

  const CameraParameters * cam = static_cast<const CameraParameters *>(parameter(0));

  Matrix<double,2,3,Eigen::ColMajor> tmp;
  tmp(0,0) = cam->focal_length;
  tmp(0,1) = 0;
  tmp(0,2) = -x/z*cam->focal_length;

  tmp(1,0) = 0;
  tmp(1,1) = cam->focal_length;
  tmp(1,2) = -y/z*cam->focal_length;

  _jacobianOplusXi =  -1./z * tmp * T.rotation().toRotationMatrix();

  _jacobianOplusXj(0,0) =  x*y/z_2 *cam->focal_length;
  _jacobianOplusXj(0,1) = -(1+(x*x/z_2)) *cam->focal_length;
  _jacobianOplusXj(0,2) = y/z *cam->focal_length;
  _jacobianOplusXj(0,3) = -1./z *cam->focal_length;
  _jacobianOplusXj(0,4) = 0;
  _jacobianOplusXj(0,5) = x/z_2 *cam->focal_length;

  _jacobianOplusXj(1,0) = (1+y*y/z_2) *cam->focal_length;
  _jacobianOplusXj(1,1) = -x*y/z_2 *cam->focal_length;
  _jacobianOplusXj(1,2) = -x/z *cam->focal_length;
  _jacobianOplusXj(1,3) = 0;
  _jacobianOplusXj(1,4) = -1./z *cam->focal_length;
  _jacobianOplusXj(1,5) = y/z_2 *cam->focal_length;
}

　　5）g2o初始化

　　　　5.1） BlockSolver 模板参数初始化（顶点的维度信息）

typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block;  // pose 维度为 6, landmark 维度为 3

　　　　5.2）初始化中设置线性求解器（求解方法）

　　6）增加边信息（位姿和特征点位置）

　　7) 增加参数信息：相机的内存

　　8) 增加边：

　　　　先设置ID，其次设置该边连接的顶点信息，设置量测信息，设置连接的参数信息，

　　9）启动优化

参考链接

《视觉SLAM十四讲精品总结》7：VO—— 3D-2D：PnP+BA

代码

#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/calib3d/calib3d.hpp>
#include <Eigen/Core>
#include <Eigen/Geometry>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/csparse/linear_solver_csparse.h>
#include <g2o/types/sba/types_six_dof_expmap.h>
#include <chrono>

using namespace std;
using namespace cv;

void find_feature_matches (
    const Mat& img_1, const Mat& img_2,
    std::vector<KeyPoint>& keypoints_1,
    std::vector<KeyPoint>& keypoints_2,
    std::vector< DMatch >& matches );

// 像素坐标转相机归一化坐标
Point2d pixel2cam ( const Point2d& p, const Mat& K );

void bundleAdjustment (
    const vector<Point3f> points_3d,
    const vector<Point2f> points_2d,
    const Mat& K,
    Mat& R, Mat& t
);

int main ( int argc, char** argv )
{
    if ( argc != 5 )
    {
        cout<<"usage: pose_estimation_3d2d img1 img2 depth1 depth2"<<endl;
        return 1;
    }
    //-- 读取图像
    Mat img_1 = imread ( argv[1], CV_LOAD_IMAGE_COLOR );
    Mat img_2 = imread ( argv[2], CV_LOAD_IMAGE_COLOR );

    vector<KeyPoint> keypoints_1, keypoints_2;
    vector<DMatch> matches;
    find_feature_matches ( img_1, img_2, keypoints_1, keypoints_2, matches );
    cout<<"一共找到了"<<matches.size() <<"组匹配点"<<endl;

    // 建立3D点
    Mat d1 = imread ( argv[3], CV_LOAD_IMAGE_UNCHANGED );       // 深度图为16位无符号数，单通道图像
    Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
    vector<Point3f> pts_3d;
    vector<Point2f> pts_2d;
    for ( DMatch m:matches )
    {
        ushort d = d1.ptr<unsigned short> (int ( keypoints_1[m.queryIdx].pt.y )) [ int ( keypoints_1[m.queryIdx].pt.x ) ];
        if ( d == 0 )   // bad depth
            continue;
        float dd = d/5000.0;
        Point2d p1 = pixel2cam ( keypoints_1[m.queryIdx].pt, K );
        pts_3d.push_back ( Point3f ( p1.x*dd, p1.y*dd, dd ) );
        pts_2d.push_back ( keypoints_2[m.trainIdx].pt );
    }

    cout<<"3d-2d pairs: "<<pts_3d.size() <<endl;

    Mat r, t;
    solvePnP ( pts_3d, pts_2d, K, Mat(), r, t, false, SOLVEPNP_EPNP); // 调用OpenCV 的 PnP 求解，可选择EPNP，DLS等方法
    Mat R;
    cv::Rodrigues ( r, R ); // r为旋转向量形式，用Rodrigues公式转换为矩阵

    cout<<"R="<<endl<<R<<endl;
    cout<<"t="<<endl<<t<<endl;

    cout<<"calling bundle adjustment"<<endl;

    bundleAdjustment ( pts_3d, pts_2d, K, R, t );
}

void find_feature_matches ( const Mat& img_1, const Mat& img_2,
                            std::vector<KeyPoint>& keypoints_1,
                            std::vector<KeyPoint>& keypoints_2,
                            std::vector< DMatch >& matches )
{
    //-- 初始化
    Mat descriptors_1, descriptors_2;
    // used in OpenCV3
    Ptr<FeatureDetector> detector = ORB::create();
    Ptr<DescriptorExtractor> descriptor = ORB::create();
    // use this if you are in OpenCV2
    // Ptr<FeatureDetector> detector = FeatureDetector::create ( "ORB" );
    // Ptr<DescriptorExtractor> descriptor = DescriptorExtractor::create ( "ORB" );
    Ptr<DescriptorMatcher> matcher  = DescriptorMatcher::create ( "BruteForce-Hamming" );
    //-- 第一步:检测 Oriented FAST 角点位置
    detector->detect ( img_1,keypoints_1 );
    detector->detect ( img_2,keypoints_2 );

    //-- 第二步:根据角点位置计算 BRIEF 描述子
    descriptor->compute ( img_1, keypoints_1, descriptors_1 );
    descriptor->compute ( img_2, keypoints_2, descriptors_2 );

    //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
    vector<DMatch> match;
    // BFMatcher matcher ( NORM_HAMMING );
    matcher->match ( descriptors_1, descriptors_2, match );

    //-- 第四步:匹配点对筛选
    double min_dist=10000, max_dist=0;

    //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
    for ( int i = 0; i < descriptors_1.rows; i++ )
    {
        double dist = match[i].distance;
        if ( dist < min_dist ) min_dist = dist;
        if ( dist > max_dist ) max_dist = dist;
    }

    printf ( "-- Max dist : %f \n", max_dist );
    printf ( "-- Min dist : %f \n", min_dist );

    //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
    for ( int i = 0; i < descriptors_1.rows; i++ )
    {
        if ( match[i].distance <= max ( 2*min_dist, 30.0 ) )
        {
            matches.push_back ( match[i] );
        }
    }
}

Point2d pixel2cam ( const Point2d& p, const Mat& K )
{
    return Point2d
           (
               ( p.x - K.at<double> ( 0,2 ) ) / K.at<double> ( 0,0 ),
               ( p.y - K.at<double> ( 1,2 ) ) / K.at<double> ( 1,1 )
           );
}

void bundleAdjustment (
    const vector< Point3f > points_3d,
    const vector< Point2f > points_2d,
    const Mat& K,
    Mat& R, Mat& t )
{
    // 初始化g2o
    typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block;  // pose 维度为 6, landmark 维度为 3
    Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse<Block::PoseMatrixType>(); // 线性方程求解器
    Block* solver_ptr = new Block ( linearSolver );     // 矩阵块求解器
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );
    g2o::SparseOptimizer optimizer;
    optimizer.setAlgorithm ( solver );

    // vertex
    g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // camera pose
    Eigen::Matrix3d R_mat;
    R_mat <<
          R.at<double> ( 0,0 ), R.at<double> ( 0,1 ), R.at<double> ( 0,2 ),
               R.at<double> ( 1,0 ), R.at<double> ( 1,1 ), R.at<double> ( 1,2 ),
               R.at<double> ( 2,0 ), R.at<double> ( 2,1 ), R.at<double> ( 2,2 );
    pose->setId ( 0 );
    pose->setEstimate ( g2o::SE3Quat (
                            R_mat,
                            Eigen::Vector3d ( t.at<double> ( 0,0 ), t.at<double> ( 1,0 ), t.at<double> ( 2,0 ) )
                        ) );
    optimizer.addVertex ( pose );

    int index = 1;
    for ( const Point3f p:points_3d )   // landmarks
    {
        g2o::VertexSBAPointXYZ* point = new g2o::VertexSBAPointXYZ();
        point->setId ( index++ );
        point->setEstimate ( Eigen::Vector3d ( p.x, p.y, p.z ) );
        point->setMarginalized ( true ); // g2o 中必须设置 marg 参见第十讲内容
        optimizer.addVertex ( point );
    }

    // parameter: camera intrinsics
    g2o::CameraParameters* camera = new g2o::CameraParameters (
        K.at<double> ( 0,0 ), Eigen::Vector2d ( K.at<double> ( 0,2 ), K.at<double> ( 1,2 ) ), 0
    );
    camera->setId ( 0 );
    optimizer.addParameter ( camera );

    // edges
    index = 1;
    for ( const Point2f p:points_2d )
    {
        g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
        edge->setId ( index );
        edge->setVertex ( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> ( optimizer.vertex ( index ) ) );
        edge->setVertex ( 1, pose );
        edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );
        edge->setParameterId ( 0,0 );
        edge->setInformation ( Eigen::Matrix2d::Identity() );
        optimizer.addEdge ( edge );
        index++;
    }

    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    optimizer.setVerbose ( true );
    optimizer.initializeOptimization();
    optimizer.optimize ( 100 );
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>> ( t2-t1 );
    cout<<"optimization costs time: "<<time_used.count() <<" seconds."<<endl;

    cout<<endl<<"after optimization:"<<endl;
    cout<<"T="<<endl<<Eigen::Isometry3d ( pose->estimate() ).matrix() <<endl;
}

结果及分析

calling bundle adjustment
iteration= 0     chi2= 0.001139     time= 0.00024794     cumTime= 0.00024794     edges= 75     schur= 1     lambda= 78.084078     levenbergIter= 1
iteration= 1     chi2= 0.000000     time= 8.4022e-05     cumTime= 0.000331962     edges= 75     schur= 1     lambda= 52.056052     levenbergIter= 1
iteration= 2     chi2= 0.000000     time= 7.3859e-05     cumTime= 0.000405821     edges= 75     schur= 1     lambda= 34.704035     levenbergIter= 1
iteration= 3     chi2= 0.000000     time= 7.2104e-05     cumTime= 0.000477925     edges= 75     schur= 1     lambda= 23.136023     levenbergIter= 1
iteration= 4     chi2= 0.000000     time= 7.1545e-05     cumTime= 0.00054947     edges= 75     schur= 1     lambda= 15.424015     levenbergIter= 1
iteration= 5     chi2= 0.000000     time= 7.1754e-05     cumTime= 0.000621224     edges= 75     schur= 1     lambda= 10.282677     levenbergIter= 1
iteration= 6     chi2= 0.000000     time= 7.1703e-05     cumTime= 0.000692927     edges= 75     schur= 1     lambda= 6.855118     levenbergIter= 1
iteration= 7     chi2= 0.000000     time= 7.1395e-05     cumTime= 0.000764322     edges= 75     schur= 1     lambda= 4.570079     levenbergIter= 1
iteration= 8     chi2= 0.000000     time= 7.2222e-05     cumTime= 0.000836544     edges= 75     schur= 1     lambda= 9.140157     levenbergIter= 1
optimization costs time: 0.00163647 seconds.

after optimization:
T=
  0.997848 -0.0510879  0.0410952  -0.128454
 0.0499059   0.998324  0.0292911 -0.0103276
-0.0425228 -0.0271772   0.998726  0.0590494
         0          0          0          1

　　相比PnP的结果，在小数点第三位会有区别。(主要原因是将位姿和特征点统一放进去一起进行最优化估计)

posted @ 2021-07-30 11:39 博客园—哆啦A梦阅读(1686) 评论(0) 收藏举报

刷新页面返回顶部

博客园—哆啦A梦

视觉SLAM 十四讲——3D-2D:PnP求解——BA

主要内容

参考链接

代码

结果及分析

公告