统计学习方法c++实现之五 逻辑斯蒂回归
逻辑回归
前言
最早接触逻辑回归是在学习吴恩达老师的机器学习课程的时候,那个时候逻辑回归是跟在线性回归后面出现的,当时感觉这应该就是个“hello world”级别的机器学习模型(好像确实是),现在看到《统计学习方法》中的各种推导,才发现自己了解的太少,静下心来看逻辑回归模型和最大熵模型,发现确实蕴藏了很多统计学的基本原理,但是这系列博客重点是实现,所以这里就不进行推导了,书中讲的很详细了。代码地址https://github.com/bBobxx/statistical-learning/blob/master/src/logistic.cpp
逻辑回归的基本概念
逻辑回归是一种分类模型,一般是二分类,书中给出了逻辑斯蒂分布的概率分布函数和图像,在机器学习中,我们需要得到的是条件概率分布,以二分类为例:
$ P(Y=1|x) = \frac{exp(wx)}{1+exp(wx)}$
$P(Y=0|x) = 1-P(Y=1|x) $
当然一般形式是采用Sigmoid函数那种形式:
$ P(Y=1|x) = \frac{1}{1+e^{-wx}}$
两种形式是相等的,这里的w是将偏移量b加入w后的向量,相应的x应该扩充为\((x_1,x_2,...,x_n, 1)\)。我们的目的是估计w的值。
模型的估计使用最大似然估计,对数似然函数:
$L(w)=\sum_i[y_ilogP(Y=1|x)+(1-y_i)log(1-P(Y=0|x)] $
我们的目的就是求出让\(-L(w)\)最小的w,这里我们选择使用梯度下降法。
模型的概念介绍的比较简单,大家看代码就能看懂,这里就不赘述了。
代码实现
代码结构图
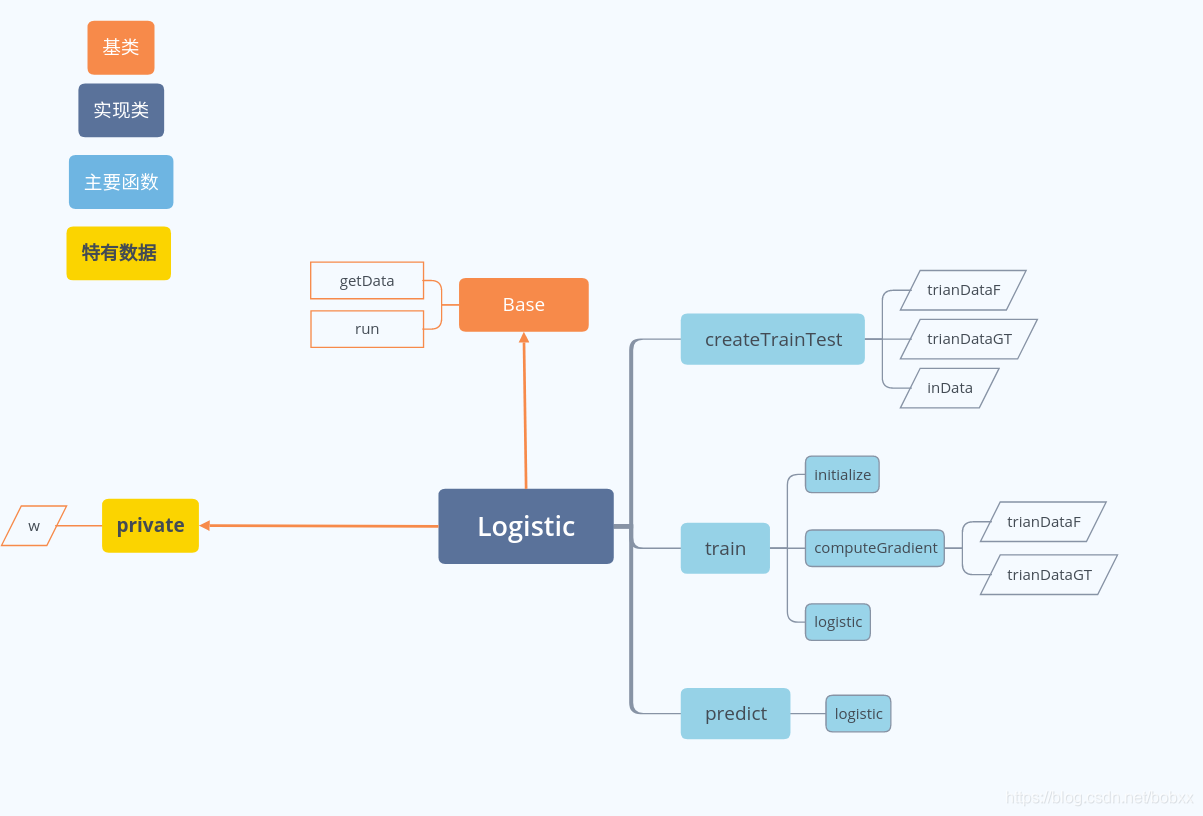
核心代码展示
void Logistic::train(const int& step, const double& lr) {
int count = 0;
for(int i=0; i<step; ++i) {
if (count == trainDataF.size() - 1)
count = 0;
count++;
vector<double> grad = computeGradient(trainDataF[count], trainDataGT[count]);
double fl;
if (trainDataGT[count]==0)
fl = 1;
else
fl = -1;
w = w + fl*lr*grad;
auto val = trainDataF[count]*w;
double loss = -1*trainDataGT[count]*val + log(1 + exp(val));
cout<<"step "<<i<<", train loss is "<<loss<<" gt "<<trainDataGT[count]<<endl;
}
}
上面的w优化的时候根据类别确定了梯度的正负(其实是确定要加上这部分梯度还是减去),这个是公式上没出现的。我的理解是前面计算梯度的公式在向量应用的时候有点问题,这部分如果有疑问就深入讨论。



