作业_2018.08.25

A. qhy的锐角三角形

前置技能： 圆周角相关，高斯求和公式，组合
推公式

B. qhy的目标

矩阵快速幂注意要点：

变量的值莫名变了，可能是数组越界影响其他变量
矩乘不满足交换率 ，但可以顺着写
局部不能更全局变量？
记得两种初始化【清空和对角元】，而且不能在结构体
数组是指针变参？
每个矩阵注意不要漏元素没有填

C. qhy的橘猫

坑

D. [AHOI2017初中组]alter

这个\(check(mid)\)这么写
我们假设不重复花费机会，那么花最少机会的就是，尽量越往后使用，否则可能会比不这么做增长连续序列的长度，这对我们是不利的，但是要注意因为是在\(mid + 1\)为发现超过\(mid\) ，如果\(mid+2\) 刚好是相反的，直接改\(mid + 1\)会延长后面的相反区间的长度，所以这时改\(mid\)处

AT
这样又可能使得\(mid == 1\)时，修改\(mid\)会延长前面的，又各种后效性，

所以直接把\(1\)的情况提出来规定一个\(0-1\)序列写\(xor\)然后再反过来搞一遍

题目说剩下的机会不一定是要用完滴
【各位julao们都用公式 %%%%

E. [AHOI2018初中组]分组

子任务搞法搞不动？来敲敲正解比啊

暴力

有个\(n^2\)的做法，\(a[i]\)每次给已知最少的组能接的接长

优化暴力

思维难度相对小但是用到了STL里的priority_queue和map. 从小到大加入每一个元素， 每次贪心地找到上一个元素是X-1的组并加入这个元素， 如果有多个，加入元素数量最小的那个组； 如果没有，则创建一个新组，组内元素只有X. 具体实现，可以用map套priority_queue实现， map维护的组内的上一个元素，pq维护的是满足条件的所有组的大小. 离散化后开O(n)个priority_queue也是可行做法.
复杂度\(nlogn\)

二分答案

每次强制取\(l\)个连续的，取不到的话考虑拼到前面，辅助数组搞一下ok
复杂度\(nlogn\)

贪心

qwq很接近刚开始我的想法，无奈还是太菜(

将所有人的实力值放进一个桶里，
每次考虑将没有分配的人中实力值最小的那个人提出来，单独为一个组

假设这个人的实力值是\(p\)，把这个人放入当前组， 按照\(p+1,p+2 \cdots x\)依次遍历实力值， 依次把每个桶里选一个放进这个组，假设当前遍历到是\(x\)，当剩余的实力值为\(x\)的人数小于实力值为\(x-1\)的人数【有下降的趋势】，则让这一组最大元素为\(x-1\)，这个组就分配完了

这样不断取出元素直到所有元素都被分组，此时人数最少的组就是最优解.

==做法正确性证明：
剩余的实力值为\(x\)的人数小于实力值为\(x-1\)的人数\(<=>\)定有一组中实力值最大的实力值\(Max\)为\(x-1\)即以\(x-1\)结尾；

然后易知每次新的小组的\(Min\)单调不下降，\(Max\)也是如此，所以组的大小\(|Max-Min+1|\)可以显然达到最优

==离散化注意
对于\(|A_i| \leq 10^9\)无法直接存到一个桶里的情况， 将实力值排序后离散化，对于不连续的实力值中间加上一个容积为\(0\)的桶 \(注意两倍数组\)

时间复杂度O(nlogn).

【貌似来自官方题解2333

F. 仓鼠找sugar

刚开始看错题 。。。
由于在树上中要有相交的路径的话，\(a->b\)和\(c->d\)
中，交点为至少一条路径的\(lca\)，因为交点只有一个爸爸，又不能是两个\(lca\)的共同儿子，而且\(lca\)也不会是他的儿子。

对相交的情况分类
情况一：
\(lca(a,b)=lca(c,d)\)这时显然有交点
情况二：
三个点在一棵子树，另外一个点在另一棵子树
假设\(lca(a,b)\)为交点，显然\(c,d\)中有一个应当为\(lca(a,b)\)的儿子或孙子，这里有\(2\)种情况，假设这个点为\(c\)，根据对称性易知\(a,b\)中至少有一个点，假设为\(a\)，那么满足\(lca(a,c) = lca(a,b)\)，如下图所示

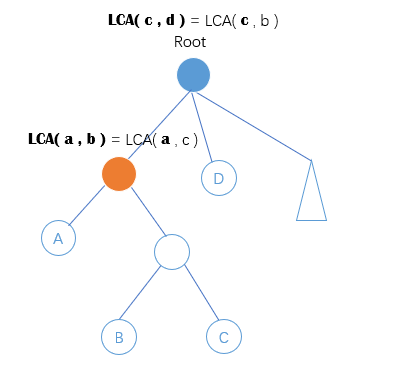
由于\(a,b\)也有两种情况，所以根据乘法原理，这里共有\(4\)种情况

G. 组合数问题 125E591

脑子是个好东西(
首先涨点姿势，对于\(C_n^r\)可以求它的对数，要用double保存，不影响比较大小

\[ \begin{align*} ln(C_n^r) &= ln(\dfrac{n!}{m!(n-m)!})\\ &= ln(n!) - ln(m!) - ln((n-m)!)\\ &= \sum_{i=1}^n ln(i) - \sum_{i=1}^m ln(i) - \sum_{i=1}^{n-m} ln(i) \end{align*} \]

这就可以直接用了
上式还可以化成$$\sum_{i=1}^m ln(i) + \sum_{i=n-m+1}^n ln(i) - \sum_{i=1}^m ln(i) - \sum_{i=1}^{n-m} ln(i) = \sum_{i=n-m+1}^n ln(i) - \sum_{i=1}^{n-m} ln(i)$$虽然还是得用前缀和
还有exp和ln为互逆函数
来自大数量级组合数的计算方法

貌似暴力求log前缀和的常数比较大，使用线性筛可以解决这个问题？

然后标程告诉我们可重集的排序是不需要去重的
所以我们定义一个二元组\((x,y)\)表示\(C_x^y\)，根据对称性也就是杨辉三角左半部分的坐标对应的组合数，先把中间的全加进去，然后用堆维护一下就可以了

注意：\(k\)表示还要取出\(k\)个数，每次取出一个数相当于取出两个数k-=2，看成是把左右对称的两个绑在一个包加进去，隔行相同的情况因为会添加多个包所以没问题，除了当\(odd(n + 1)\)时，就是\(n\)为偶数时，中间的数是唯一的以及k=1时特判一下
int是20亿左右，2e10左右

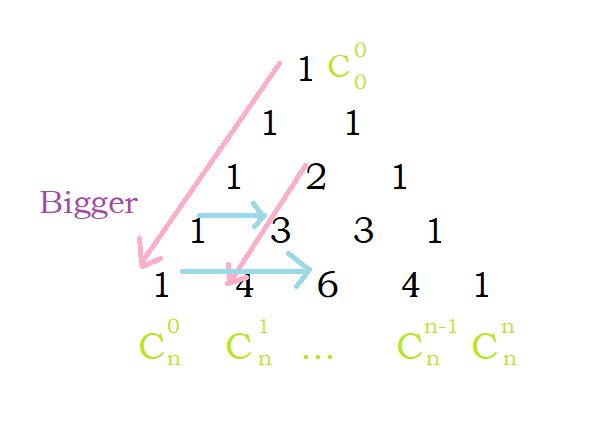
由于懒得学STL然后学了下斜堆23333