NOIP2008pj & luoguP1058 立体图 模拟
题目描述
小渊是个聪明的孩子,他经常会给周围的小朋友们将写自己认为有趣的内容。最近,他准备给小朋友们讲解立体图,请你帮他画出立体图。
小渊有一块面积为m*n的矩形区域,上面有m*n个边长为1的格子,每个格子上堆了一些同样大小的积木(积木的长宽高都是1),小渊想请你打印出这些格子的立体图。我们定义每个积木为如下格式,并且不会做任何翻转旋转,只会严格以这一种形式摆放:
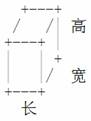
每个顶点用1个加号’+’表示,长用3个”-”表示,宽用1个”/”,高用两个”|”表示。字符’+’,”-”,”/”,”|”的ASCII码分别为43,45,47,124。字符’.’(ASCII码46)需要作为背景输出,即立体图里的空白部分需要用’.’来代替。立体图的画法如下面的规则:
若两块积木左右相邻,图示为:
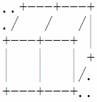
若两块积木上下相邻,图示为:
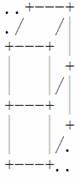
若两块积木前后相邻,图示为:

立体图中,定义位于第(m,1)的格子(即第m行第1列的格子)上面自底向上的第一块积木(即最下面的一块积木)的左下角顶点为整张图最左下角的点。
输入输出格式
输入格式:
输入文件drawing.in第一行有用空格隔开的2个整数m和n,表示有m*n个格子(1<=m,n<=50)。
接下来的m行,是一个m*n的矩阵,每行有n个用空格隔开的整数,其中第i行第j列上的整数表示第i行第j列的个子上摞有多少个积木(1<=每个格子上的积木数<=100)。
输出格式:
输出文件drawing.out中包含题目要求的立体图,是一个K行L列的字符串矩阵,其中K和L表示最少需要K行L列才能按规定输出立体图。
输入输出样例
3 4 2 2 1 2 2 2 1 1 3 2 1 2
......+---+---+...+---+ ..+---+ / /|../ /| ./ /|-+---+ |.+---+ | +---+ |/ /| +-| | + | | +---+ |/+---+ |/| | |/ /| +/ /|-+ | +---+---+ |/+---+ |/| + | | | +-| | + |/. | | |/ | |/| +.. +---+---+---+---+ |/... | | | | | +.... | | | | |/..... +---+---+---+---+......
说明
NOIP2008普及组第四题
思路
补题中。。。
咳咳,题目非常亲民啊2333
模拟赛(模拟大赛qwq)时差点就打粗来了,结果还以为自己是错的就弃疗了【忧桑
因为我们看到的是这个立方体的前面右面和上面,
所以我们只要从左往右,从下往上,从后往前,就可以了
先把画布清一色的背景填充好
然后计算画布最左下角的坐标s_hang,s_lie和画布大小k,l
然后在画得时候计算找到每个方块左上角绘制就可以了
具体怎么计算呢?

哦,还有,就是在绘制的时候如果是'.'就不绘制了。。
代码
第一次用cpp打题,好激动
1 #include<iostream> 2 #include<cstring> 3 using namespace std; 4 char power[6][8]={ 5 "..+---+", 6 "./ /|", 7 "+---+ |", 8 "| | +", 9 "| |/.", 10 "+---+.." 11 }; 12 char mmap[1000][1000]; 13 int n,m; 14 int a[1000][1000]; 15 int k,l,s_hang,s_lie; 16 17 void outgo(){ 18 for (int i=1;i<=k;i++) 19 { 20 for (int j=1;j<=l;j++) 21 printf("%c",mmap[i][j]); 22 printf("\n"); 23 } 24 } 25 26 void draw(int i,int j,int k){ 27 int lie=s_lie+2*(m-i)+4*(j-1); 28 int hang=s_hang-(m-i+1)*2-3*k; 29 30 for (int i=0;i<=5;i++) 31 for (int j=0;j<=6;j++) 32 { 33 if (power[i][j]!='.') mmap[hang+i][lie+j]=power[i][j]; 34 } 35 // outgo(); 36 } 37 38 void init(){ 39 memset(mmap,'.',sizeof(mmap)); 40 scanf("%d %d",&m,&n); 41 l=4*n+1+2*m; 42 for (int i=1;i<=m;i++) 43 for (int j=1;j<=n;j++) 44 { 45 scanf("%d",&a[i][j]); 46 k=max(k,3*a[i][j]+1+2*(m-i+1)); 47 } 48 s_hang=k; s_lie=1; 49 for (int i=1;i<=m;i++) 50 for (int j=1;j<=n;j++) 51 for (int k=1;k<=a[i][j];k++) 52 draw(i,j,k); 53 } 54 55 int main(){ 56 57 freopen("drawing.in","r",stdin); 58 freopen("drawing.out","w",stdout); 59 init(); 60 outgo(); 61 fclose(stdin); 62 fclose(stdout); 63 64 return 0; 65 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号