NOIP2016 PJ T4 魔法阵

魔法阵

题目描述

六十年一次的魔法战争就要开始了，大魔法师准备从附近的魔法场中汲取魔法能量。

大魔法师有m个魔法物品，编号分别为1,2,...,m。每个物品具有一个魔法值，我们用Xi表示编号为i的物品的魔法值。每个魔法值Xi是不超过n的正整数，可能有多个物品的魔法值相同。

大魔法师认为，当且仅当四个编号为a,b,c,d的魔法物品满足xa<xb<xc<xd，Xb-Xa=2(Xd-Xc)，并且xb-xa<(xc-xb)/3时，这四个魔法物品形成了一个魔法阵，他称这四个魔法物品分别为这个魔法阵的A物品，B物品，C物品，D物品。

现在，大魔法师想要知道，对于每个魔法物品，作为某个魔法阵的A物品出现的次数，作为B物品的次数，作为C物品的次数，和作为D物品的次数。

输入输出格式

输入格式：

输入文件的第一行包含两个空格隔开的正整数n和m。

接下来m行，每行一个正整数，第i+1行的正整数表示Xi，即编号为i的物品的魔法值。

保证,,。每个Xi是分别在合法范围内等概率随机生成的。

输出格式：

共输出m行，每行四个整数。第i行的四个整数依次表示编号为i的物品作 为A,B,C,D物品分别出现的次数。

保证标准输出中的每个数都不会超过10^9。

每行相邻的两个数之间用恰好一个空格隔开。

输入输出样例

输入样例#1：

30 8
1
24
7
28
5
29
26
24

输出样例#1：

4 0 0 0
0 0 1 0
0 2 0 0
0 0 1 1
1 3 0 0
0 0 0 2
0 0 2 2
0 0 1 0

输入样例#2：

15 15
1 
2 
3 
4 
5
6 
7 
8 
9
10
11
12
13
14
15

输出样例#2：

5 0 0 0
4 0 0 0
3 5 0 0
2 4 0 0
1 3 0 0
0 2 0 0
0 1 0 0
0 0 0 0
0 0 0 0
0 0 1 0
0 0 2 1
0 0 3 2
0 0 4 3
0 0 5 4
0 0 0 5

说明

【样例解释1】

共有5个魔法阵，分别为：

物品1,3,7,6，其魔法值分别为1,7,26,29;

物品1,5,2,7，其魔法值分别为1,5,24,26;

物品1,5,7,4，其魔法值分别为1,5,26,28;

物品1,5,8,7，其魔法值分别为1,5,24,26;

物品5,3,4,6，其魔法值分别为5,7,28,29。

以物品5为例，它作为A物品出现了1次，作为B物品出现了3次，没有作为C物品或者D物品出现，所以这一行输出的四个数依次为1,3,0,0。

此外，如果我们将输出看作一个m行4列的矩阵，那么每一列上的m个数之和都应等于魔法阵的总数。所以，如果你的输出不满足这个性质，那么这个输出一定不正确。你可以通过这个性质在一定程度上检查你的输出的正确性。

【数据规模】

 

 

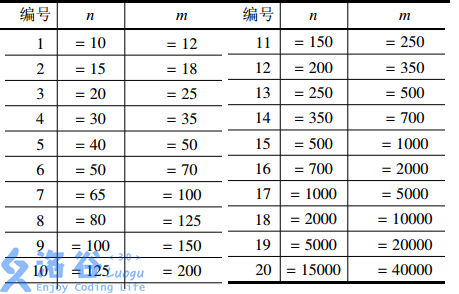
思路

85分做法：

注：本文主体是lz在校运会时偷偷溜到机房写的。。。。。

可以知道一个魔法阵的条件
(1)a < b < c < d
(2)b - a = 2(d - c)
    由此，我们设d-c=i 那么 b-a=2*i;
(3)b - a < (c - b) / 3
  so 2*i<(c-b)/3
解得:6*i<c-b

再设 6*i+k=c-b

得图：

大招放！ 枚举a ,i [可以得到b],k [可以得到c,然后继而得到d!]

 

P.S. 屁嘞，说了这么多你的枚举范围呢？

 

QwQ枚举的范围 啊？
a的范围自然是1--->n
嗯，由刚才的结论得：d-a=(b-a)+(c-b)+(d-c)=2*i+6*i+k+i=9*i+k——（1）式
那么i 的范围: 1--->(n-a-1)/9     //因为a<b<c<d<=n,k最小为1
所以k的范围:因为（1）式d-a=9*i+k, 而且n>=a，所以k最大为n-a-9*i     , 最小为1

 

当然你也可以用其他方法拿到85分，比如你可以枚举n-d的距离，然后枚举i,再枚举k， 我的另外一种85分

然后是简单的代码：

program ac85;
var
  n,m,i,k,a,b,c,d:longint;
  p,x:array[1..40000]of longint;
  ans:array[1..15000,1..4]of longint;
begin

  assign(input,'magic.in');reset(input);
  assign(output,'magic.out');rewrite(output);
  readln(n,m);
  for i:= 1 to m do
  begin
    read(x[i]);
    inc(p[x[i]]);
  end;

  for a:= 1 to n do
   if p[a]<>0 then
    for i:= 1 to (n-a-1) div 9 do
      begin
         b:=a+2*i;
         if p[b]=0 then continue;
         for k:= 1 to  n-a-9*i do
           begin
             c:=b+6*i+k;
             if p[c]=0 then continue;
             d:=c+i;
             if p[d]=0 then continue;
             ans[a,1]:=ans[a,1]+p[b]*p[c]*p[d];
             ans[b,2]:=ans[b,2]+p[a]*p[c]*p[d];
             ans[c,3]:=ans[c,3]+p[a]*p[b]*p[d];
             ans[d,4]:=ans[d,4]+p[a]*p[b]*p[c];//乘法原理，因为当前已经确定那么其他三个相乘就是此时这种情况下的种数
           end;
       end;
   for i:=1 to m do
      writeln(ans[x[i],1],' ',ans[x[i],2],' ',ans[x[i],3],' ',ans[x[i],4]);
  close(input);
  close(output);

end.

 

100分做法

 

 因为通过上面85分的做法我们知道只要知道 a,i,k ，就可以算。。。

 但是如果我们反过来  

我们先枚举d，i，当然我们得到了c ，那么在枚举k 就是求a,b

当前c的方案种数=(当前魔法值等于d的魔法物品总量)*(前面得到的若干个a 的魔法物品总量)*(前面得到的若干个b 的魔法物品总量)

当前d的方案种数=(当前魔法值等于c的魔法物品总量)*(前面得到的若干个a 的魔法物品总量)*(前面得到的若干个b 的魔法物品总量)

因为要枚举k，每次枚举时把得到的a和b的乘积乘以c +到ans[c,3] ，以及把得到的a和b的乘积乘以d +到ans[d,4]里面 ,那么机制的你是不是马上想起了前缀和后缀和一类的东西QwQ，这就是前缀和啊;

//图中第二次的c和d加的sum是不是包含上次的c和d加的sum啊,这样在d往后推移的过程中，每次都加最小的a*b*(c或d)和更前面的sum啊

那同理，我们用同样的方法来求c和d的ans：

假设我们已经枚举了a和i，当然我们也得到了b，那么再枚举k 就是求c,d            

那么得：//注：当前的***表示这个***是已知的，后面的***表示我们在枚举若干k后才得到的

当前a的方案种数=(当前魔法值等于b的魔法物品总量)*(后面得到的若干个c 的魔法物品总量)*(后面得到的若干个d 的魔法物品总量)

当前b的方案种数=(当前魔法值等于a的魔法物品总量)*(后面得到的若干个c 的魔法物品总量)*(后面得到的若干个d 的魔法物品总量)

因为要枚举k，每次枚举时把得到的c和d的乘积乘以b +到ans[a,1] ，以及把得到的c和d的乘积乘以a +到ans[b,2]里面 ，这就是后缀和啊,

 

那么复杂度是多少啊？O(n^2),还会炸？不会，因为这里的n指的是i ，即题目的n div 9；233333

 

那么怎么实现啊？

可以发现用前缀和和后缀和都要枚举 i 是吧，那我们外层循环就枚举i ,内层循环分别 a和d 并求前缀和以及后缀和就可以了

 

Q：还有范围呢？

A：。。。

i的话1 到 (n-1) div 9

d的话最小就是最小为(9*i+2)，最大为n //a最小为1 ，k最小为1  d为a+9*i+k=9*i+2

a的话最大肯定是(n-9*i-1) ，最小为1 //k最小为1啊！！！Important

 

Q：为啥不用判断p[a]=0之类的。。。

A：因为等于0乘积也是0加起来等于没加啊

 

Codes:

 

program magic;
var
  n,m,i,k,a,b,c,d,minad,sum:longint;
  p,x:array[1..40000]of longint;
  ans:array[1..15000,1..4]of longint;
begin

  assign(input,'magic.in');reset(input);
  assign(output,'magic.out');rewrite(output);
  readln(n,m);
  for i:= 1 to m do
  begin
    read(x[i]);
    inc(p[x[i]]);
  end;

  for i:= 1 to (n-1) div 9 do                //外层枚举c到d的距离 i
  begin
    minad:=1+9*i;                           //a到d的最小距离
    sum:=0;
    for d:= 9*i+2 to n do                    //枚举d 为什么顺着来呢？因为前缀和是从前往后的哇，枚举d就是为了求前缀和啊
    begin
      sum:=sum+p[d-minad]*p[d-minad+2*i];    //求a*b的前缀和，d-minad=a ,d-minad+2*i=b
      c:=d-i;                                //此时的c ,  注意i已经在外层枚举
      inc(ans[d,4],sum*p[c]);                //此时d的种数，
      inc(ans[c,3],sum*p[d]);                //此时c的种数
    end;
    sum:=0;
    for a:= n-9*i-1 downto 1 do              //枚举a 为什么downto呢？因为后缀和是从后往前的哇,枚举a就是为了求后缀和啊
    begin
      b:=a+2*i;
      sum:=sum+p[a+minad]*p[a+minad-i];      //求c*d的后缀和 ,a+minad=d,a+minad-i=c
      inc(ans[a,1],sum*p[b]);                //此时a的种数
      inc(ans[b,2],sum*p[a]);                //此时b的种数
    end;
  end;
   for i:=1 to m do
      writeln(ans[x[i],1],' ',ans[x[i],2],' ',ans[x[i],3],' ',ans[x[i],4]);
  close(input);
  close(output);
end.