Mixing Chemicals

题目描述

实验室有n瓶化学药品，编号为0到n-1，你知道第i瓶只有和第c[i]瓶放在一起才会发生爆炸。为了整理实验室，你需要将他们装进k个不同的盒子里。显然，为了你的生命安全，你不能把两瓶会造成爆炸的药品放进同一个箱子。你希望计算出有多少中不同的方案。为了降低难度，你只需要将答案mod 1000000007。

输入

第一行一个整数T，表示有T组测试数据。
对于每组数据
第一行两个整数n，k
第二行n个整数表示c[i] 

输出

对于每组数据输出一行一个整数。

样例输入

3

3 3

1 2 0

4 3

1 2 0 0

3 2

1 2 0 

样例输出

6

12

0 

数据范围限制

【数据范围】
 1<=T<=50
 1<=n<=100
 2<=k<=1000
0<=c i <n,i≠c[i]
对于30%的数据T,n,k<=50

 

 爆零。。。

 

题目来自 BestCoder Round #71 (div.2)

官方题解：

根据药品之间的相互关系，我们可以构建一张图，我们对相互会发生反应的药品连边  //连边表示他们两个化学药品不能在一起

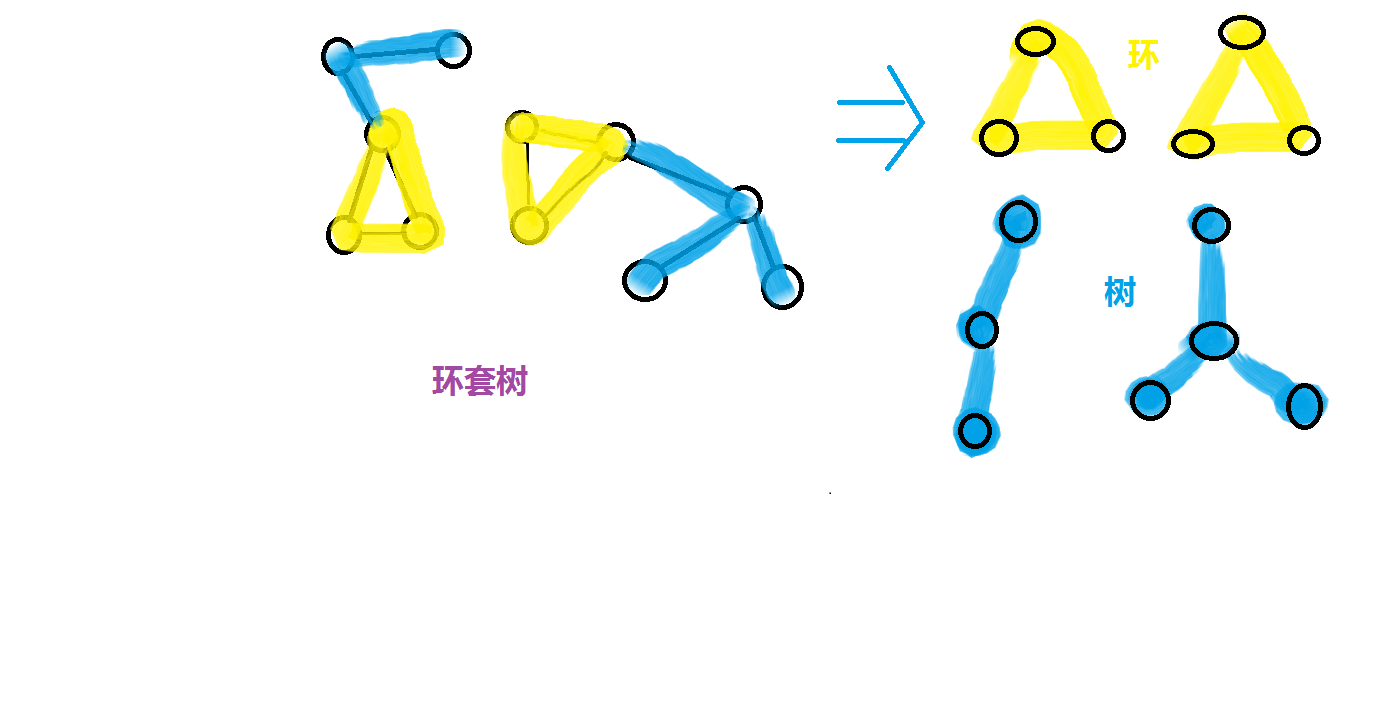
这个图的特征，是一个环加上一些“树”（可能有多个联通块）//如这么一个图

一个环（1,2,3,4,5……，n）m染色的方案数：递推，设第一个点颜色为1

f[I,1]表示i点颜色为1的种数，f[I,0]为颜色不为1时(不考虑n与1颜色不同)

则F[I,0]=f[i-1,0]*(m-2)+f[i-1,1]*(m-1)，F[I,1]=f[i-1,0]

那么方案数为f[n,0]*m

一个根节点颜色固定且有k个孩子的树的m染色的方案数={(m-1)}^{k}(m?1)?k??,因为每个点的颜色只要与他的父亲颜色不同，即m-1种

因为乘法原理，一个联通块的方案数=环方案数*以环上每个点为根的树的积。多个联通块，再连乘即可。

 

 

 1 {
 2     by @bobble !
 3                     2017-1-21
 4 }
 5 program mix;
 6 const
 7   inf='mix.in';
 8   outf='mix.out';
 9   wtf=1000000007;
10 var
11    n,k,j,i,t:longint;
12    apple,tmp,ans,u,ltk:int64;
13    a:array[0..100] of longint;
14    b:array[0..100] of longint;
15    boo:boolean;
16    f:array[0..100,0..1]  of int64;
17 
18 begin
19   assign(input,inf);
20   assign(output,outf);
21   reset(input); rewrite(output);
22 
23   readln(t);
24  for j:= 1 to t do
25  begin
26    fillchar(a,sizeof(a),false);
27    fillchar(b,sizeof(b),0);
28 
29    readln(n,k);
30    f[1,0]:=k-1;    f[0,1]:=1;
31      for i:= 2 to n do
32        begin
33           f[i,0]:=(f[i-1,1]*(k-1)+f[i-1,0]*(k-2)) mod wtf;
34           f[i,1]:=(f[i-1,0]) mod wtf ;
35        end;
36    for i:= 0 to n-1 Do
37    begin
38      read(a[i]);
39      b[i]:=233;
40    end;
41 
42    apple:=0;
43    ans:=1;
44    for i:= 0 to n-1 do
45      if b[i]=233 then
46      begin
47            tmp:=i;
48            while b[tmp]=233 do
49              begin
50                  b[tmp]:=i;
51                  tmp:=a[tmp];
52              end;
53            if b[tmp]<>i then continue;
54            ltk:=0;  u:=tmp;
55         repeat
56           inc(ltk);
57           tmp:=a[tmp];
58         until tmp=u;
59 
60            ans:=ans*(f[ltk,1]*k mod wtf) mod wtf;
61         apple:=apple+ltk;
62      end;
63      n:=n-apple;
64      for i:= 1 to n do
65        ans:=ans*(k-1) mod wtf;
66     writeln(ans);
67  end;
68 
69   close(input);
70   close(output);
71 end.

 

posted @ 2017-01-21 17:50  bobble  阅读(205)  评论(0)  编辑  收藏  举报