图总结
一.思维导图
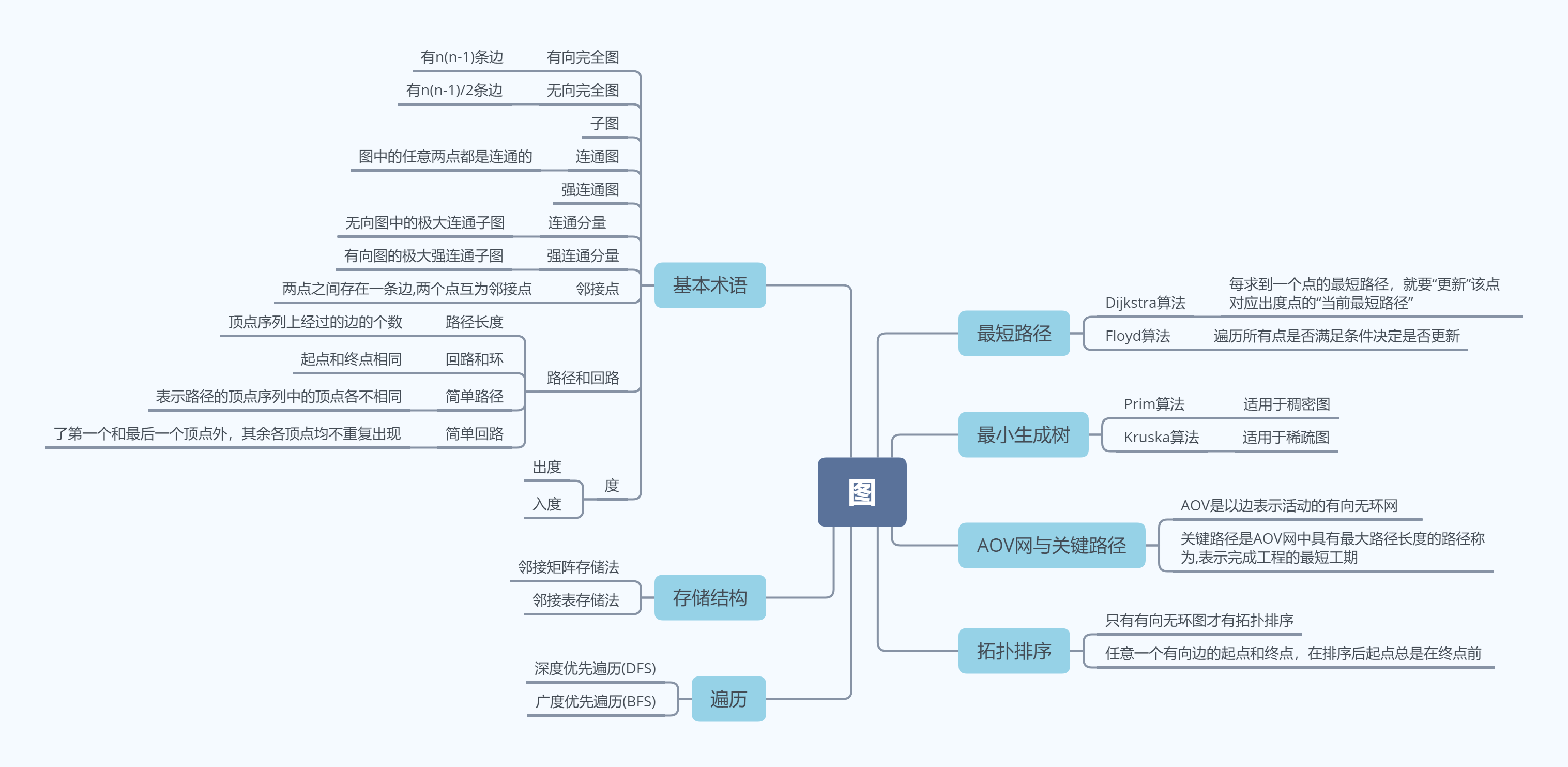
二.概念笔记
图的存储结构
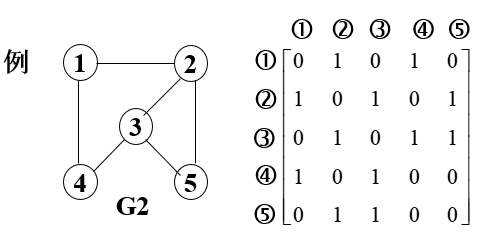
1. 邻接矩阵
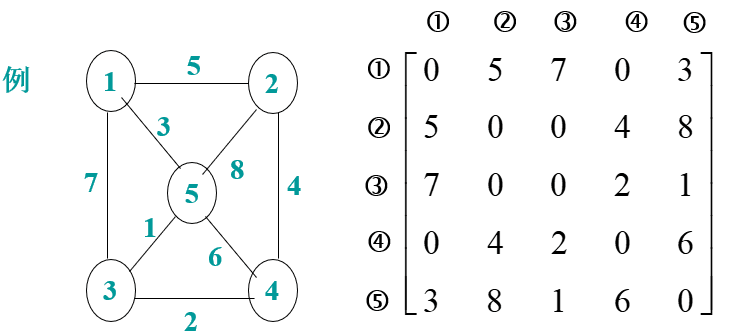
定义：设图G有n (n大于等于1) 个顶点，则邻接矩阵是一个n阶方阵。
当矩阵中的 [i,j] !=0（下标从1开始） ,代表其对应的第i个顶点与第j个顶点是连接的
特点
- 无向图的邻接矩阵是对称矩阵，n个顶点的无向图需要n*(n+1)/2个空间大小
- 有向图的邻接矩阵不一定对称，n个顶点的有向图需要n²的存储空间
- 无向图中第i行的非零元素的个数为顶点Vi的度
- 有向图中第i行的非零元素的个数为顶点Vi的出度，第i列的非零元素的个数为顶点Vi的入度
2.邻接表
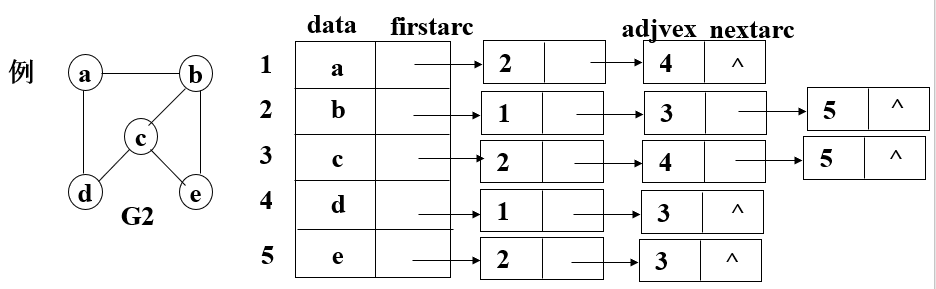
定义：为图G中的每一个顶点建立一个单链表，每条链表的结点元素为与该顶点连接的顶点
特点
- 无向图顶点Vi的度为第i个单链表中的结点数无向图中
- 顶点Vi的出度为第i个单链表中的结点个数
- 顶点Vi的入度为全部单链表中连接点域值是i的结点个数
图的遍历
深度优先遍历
图的深度优先遍历类似于树的前序遍历。先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点；当没有未访问过的顶点时，则回到上一个顶点，继续试探别的顶点，直到所有的顶点都被访问。
广度优先遍历
图的广度优先遍历类似于树的层次遍历。从图中某顶点出发，依次访问各个邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，直至图中所有顶点都被访问到为止。
最小生成树
Prim算法
Prim算法首先以一个结点作为最小生成树的初始结点，然后以迭代的方式找出与最小生成树中各结点权重最小边，并加入到最小生成树中。加入之后如果产生回路则跳过这条边，选择下一个结点。直至所有结点都加入到最小生成树中。
Kruskal算法
Kruskal算法在找最小生成树结点之前，需要对所有权重边做从小到大排序。将排序好的权重边依次加入到最小生成树中，如果加入时产生回路就跳过这条边，加入下一条边。当所有结点都加入到最小生成树中之后，就找出了最小生成树。
Kruskal在算法效率上是比Prim快，因为Kruskal只需一次对权重的排序就能找到最小生成树，而Prim算法需要多次对邻边排序才能找到
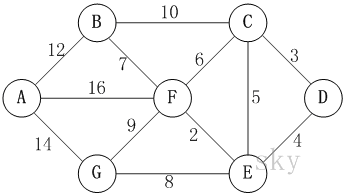
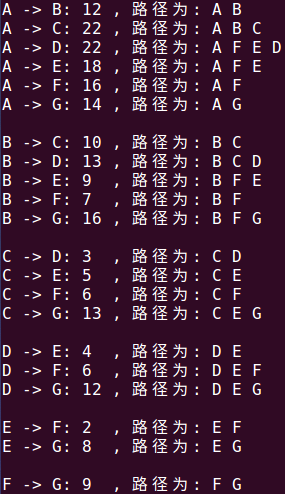
最短路径
Dijkstra算法
Dijkstra算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。
Floyd算法
Floyd算法是先找出最短的距离，然后在考虑如何找出对应的行进路线。
三.疑难问题
关于Dijkstra算法和Floyd算法的代码实现，从网上摘取两段代码理解
const int MAXINT = 32767;
const int MAXNUM = 10;
int dist[MAXNUM];
int prev[MAXNUM];
int A[MAXUNM][MAXNUM];
void Dijkstra(int v0)
{
bool S[MAXNUM]; // 判断是否已存入该点到S集合中
int n=MAXNUM;
for(int i=1; i<=n; ++i)
{
dist[i] = A[v0][i];
S[i] = false; // 初始都未用过该点
if(dist[i] == MAXINT)
prev[i] = -1;
else
prev[i] = v0;
}
dist[v0] = 0;
S[v0] = true;
for(int i=2; i<=n; i++)
{
int mindist = MAXINT;
int u = v0; // 找出当前未使用的点j的dist[j]最小值
for(int j=1; j<=n; ++j)
if((!S[j]) && dist[j]<mindist)
{
u = j; // u保存当前邻接点中距离最小的点的号码
mindist = dist[j];
}
S[u] = true;
for(int j=1; j<=n; j++)
if((!S[j]) && A[u][j]<MAXINT)
{
if(dist[u] + A[u][j] < dist[j]) //在通过新加入的u点路径找到离v0点更短的路径
{
dist[j] = dist[u] + A[u][j]; //更新dist
prev[j] = u; //记录前驱顶点
}
}
}
}
typedef struct
{
char vertex[VertexNum]; //顶点表
int edges[VertexNum][VertexNum]; //邻接矩阵,可看做边表
int n,e; //图中当前的顶点数和边数
}MGraph;
void Floyd(MGraph g)
{
int A[MAXV][MAXV];
int path[MAXV][MAXV];
int i,j,k,n=g.n;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
A[i][j]=g.edges[i][j];
path[i][j]=-1;
}
for(k=0;k<n;k++)
{
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(A[i][j]>(A[i][k]+A[k][j]))
{
A[i][j]=A[i][k]+A[k][j];
path[i][j]=k;
}
}
}
