数据结构之排序基础知识笔记

概述

最近在温习数据结构，现在针对排序算法写一篇随笔，其中附带原理说明和代码。

插入排序

直接插入排序(Straight Insertion Sort)的基本思想是：把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素，无序表中包含有n-1个元素，排序过程中每次 从无序表中取出第一个元素，将它插入到有序表中的适当位置，使之成为新的有序表，重复n-1次可完成排序过程。

假设{20,30,40,10,60,50}中的前3个数已经排列过，是有序的了；接下来对10进行排列。示意图如下：

 图中将数列分为有序区和无序区。我们需要做的工作只有两个：(1)取出无序区中的第1个数，并找出它在有序区对应的位置。(2)将无序区的数据插入到有序区；若有必要的话，则对有序区中的相关数据进行移位。

时间复杂度和稳定性

直接插入排序的时间复杂度是O(N2)。

假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢？N-1！因此，直接插入排序的时间复杂度是O(N*N)。

直接插入排序是稳定的算法，它满足稳定算法的定义。

算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的。

插入排序JAVA实现

import static javaTest.SortUtils.less;

/**
 * ClassName InsertionSort.java
 * author Rhett.wang
 * version 1.0.0
 * Description TODO
 * createTime 2020年01月16日 16:00:00
 */
public class InsertionSort implements SortAlgorithm{
    public static void main(String[] args) {
        Integer[] a= {22,14,35,45,67};
        InsertionSort sort =new InsertionSort();
        sort.sort(a);

    }
    /**
     * Main method arrays sorting algorithms
     *
     * @param array - an array should be sorted
     * @return a sorted array
     */
    @Override
    public <T extends Comparable<T>> T[] sort(T[] array) {
        for (int j = 1; j < array.length; j++) {

            // Picking up the key(Card)
            T key = array[j];
            int i = j - 1;

            while (i >= 0 && less(key, array[i])) {
                array[i + 1] = array[i];
                i--;
            }
            // Placing the key (Card) at its correct position in the sorted subarray
            array[i + 1] = key;
        }
        return array;
    }

}

实现基类接口

import java.util.Arrays;
import java.util.List;

import static javafx.scene.input.KeyCode.T;

/**
 * ClassName SortAlgorithm.java
 * author Rhett.wang
 * version 1.0.0
 * Description TODO
 * createTime 2020年01月16日 14:29:00
 */
public interface SortAlgorithm {
    /**
     * Main method arrays sorting algorithms
     *
     * @param unsorted - an array should be sorted
     * @return a sorted array
     */
    <T extends Comparable<T>> T[] sort(T[] unsorted);


    /**
     * Auxiliary method for algorithms what wanted to work with lists from JCF
     *
     * @param unsorted - a list should be sorted
     * @return a sorted list
     */
    default <T extends Comparable<T>> List<T> sort(List<T> unsorted){
       return Arrays.asList(sort(unsorted.toArray((T[]) new Comparable[unsorted.size()])));
    }
}

插入排序SCALA实现

/**
  * ClassName InsertionSort.java
  * author Rhett.wang
  * version 1.0.0
  * Description TODO
  * createTime 2020年01月18日 11:25:00
  */
object InsertionSort {
  def main(args: Array[String]) {

  }

  def sort(nums: Array[Int]): Array[Int] = {
    for (j <- 0 until nums.length -1) {
      var temp = nums(j)
      var i = j - 1
      while (i >= 0 && temp < nums(i)) {
        nums(i + 1) = nums(i)
        i-=1
      }
      nums(i + 1) = temp
    }
    nums
  }

}

插入排序PYTHON实现

def insert_sort(collection):
    """Pure implementation of the insertion sort algorithm in Python
    :param collection: some mutable ordered collection with heterogeneous
    comparable items inside
    :return: the same collection ordered by ascending
    Examples:
    >>> insertion_sort([0, 5, 3, 2, 2])
    [0, 2, 2, 3, 5]
    >>> insertion_sort([])
    []
    >>> insertion_sort([-2, -5, -45])
    [-45, -5, -2]
    """
    for loop_index in range(1,len(collection)):
        insertion_index=loop_index
        while(
            insertion_index>0
            and collection[insertion_index -1] > collection[insertion_index-1]
        ):
            collection[insertion_index],collection[insertion_index -1] =(
                collection[insertion_index -1],
                collection[insertion_index],
            )
            insertion_index -=1
    return collection

if __name__=="__main__":
     user_input= input("Enter numbers separated by a comma:\n").strip()
     unsorted=[int(item) for item in user_input.split(",")]
     print(insert_sort(unsorted))

希尔排序

希尔(Shell)排序又称为缩小增量排序，它是一种插入排序。它是直接插入排序算法的一种威力加强版。该方法因DL．Shell于1959年提出而得名，

把记录按步长 gap 分组，对每组记录采用直接插入排序方法进行排序。

随着步长逐渐减小，所分成的组包含的记录越来越多，当步长的值减小到 1 时，整个数据合成为一组，构成一组有序记录，则完成排序。

我们来通过演示图，更深入的理解一下这个过程。

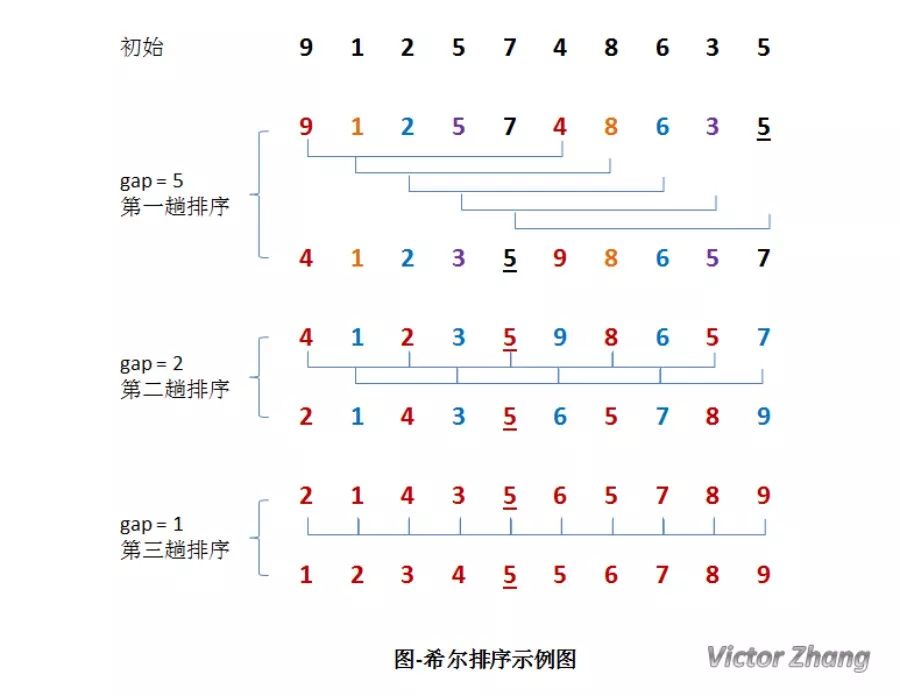
 在上面这幅图中：

初始时，有一个大小为 10 的无序序列。

在第一趟排序中，我们不妨设 gap1 = N / 2 = 5，即相隔距离为 5 的元素组成一组，可以分为 5 组。接下来，按照直接插入排序的方法对每个组进行排序。

在第二趟排序中，我们把上次的 gap 缩小一半，即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组，可以分为 2 组。按照直接插入排序的方法对每个组进行排序。

在第三趟排序中，再次把 gap 缩小一半，即gap3 = gap2 / 2 = 1。 这样相隔距离为 1 的元素组成一组，即只有一组。按照直接插入排序的方法对每个组进行排序。此时，排序已经结束。

需要注意一下的是，图中有两个相等数值的元素 5 和 5 。我们可以清楚的看到，在排序过程中，两个元素位置交换了。

所以，希尔排序是不稳定的算法。

算法分析

算法性能

 时间复杂度

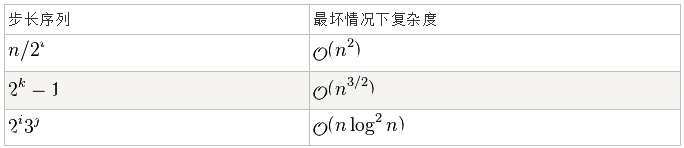
步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。

算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序，最终算法以步长为1进行排序。当步长为1时，算法变为插入排序，这就保证了数据一定会被排序。

Donald Shell 最初建议步长选择为N/2并且对步长取半直到步长达到1。虽然这样取可以比O(N2)类的算法（插入排序）更好，但这样仍然有减少平均时间和最差时间的余地。

可能希尔排序最重要的地方在于当用较小步长排序后，以前用的较大步长仍然是有序的。比如，如果一个数列以步长5进行了排序然后再以步长3进行排序，那么该数列不仅是以步长3有序，而且是以步长5有序。如果不是这样，那么算法在迭代过程中会打乱以前的顺序，那就

不会以如此短的时间完成排序了。

 算法稳定性：由上文的希尔排序算法演示图即可知，希尔排序中相等数据可能会交换位置，所以希尔排序是不稳定的算法。

插入排序和希尔排序比较：

直接插入排序是稳定的；而希尔排序是不稳定的。

直接插入排序更适合于原始记录基本有序的集合。

希尔排序的比较次数和移动次数都要比直接插入排序少，当N越大时，效果越明显。 

在希尔排序中，增量序列gap的取法必须满足：最后一个步长必须是 1 。 

直接插入排序也适用于链式存储结构；希尔排序不适用于链式结构。

希尔排序JAVA实现

import java.util.Arrays;

import static javaTest.SortUtils.less;

/**
 * ClassName ShellSort.java
 * author Rhett.wang
 * version 1.0.0
 * Description TODO
 * createTime 2020年01月18日 12:21:00
 */
public class ShellSort implements SortAlgorithm {

    /**
     * This method implements Generic Shell Sort.
     *
     * @param array the array to be sorted
     */
    @Override
    public <T extends Comparable<T>> T[] sort(T[] array) {
        int gap = array.length / 2;

        while (1 <= gap) {
            // 把距离为 gap 的元素编为一个组，扫描所有组
            for (int i = gap; i < array.length; i++) {
                int j = 0;
                T temp = array[i];

                // 对距离为 gap 的元素组进行排序
                for (j = i - gap; j >= 0 &&less(temp,array[j]); j = j - gap) {
                    array[j + gap] = array[j];
                }
                array[j + gap] = temp;
            }

            System.out.format("gap = %d:\t", gap);
            printAll(array);
            gap = gap / 2; // 减小增量
        }
        return array;
    }

    // 打印完整序列
    public <T extends Comparable<T>> void printAll(T[] list) {
        for (T value : list) {
            System.out.print(value + "\t");
        }
        System.out.println();
    }

    /* Driver Code */
    public static void main(String[] args) {
        Integer[] toSort = {4, 23, 6, 78, 1, 54, 231, 9, 12};

        ShellSort sort = new ShellSort();
        System.out.println(Arrays.toString(sort.sort(toSort)));
    }
}

希尔排序SCALA实现

package scala

/**
  * ClassName ShellSort.java
  * author Rhett.wang
  * version 1.0.0
  * Description TODO
  * createTime 2020年01月18日 13:25:00
  */
object ShellSort {
  def main(args: Array[String]) {
    var nums: Array[Int] = Array(2, 3, 8, 5, 4)
    sort(nums)
    nums.foreach(x => println(x))
  }

  def sort(nums: Array[Int]): Array[Int] = {
    var gap = nums.length / 2
    while (1 <= gap) {
      for (i <- gap until nums.length) {
        var j = i
        while (j >= 0 && nums(j-gap) > nums(j)) {
          var temp = nums(j-gap)+nums(j)
          nums(j - gap) =temp- nums(j-gap)
          nums(j)=temp- nums(j-gap)
          j=j-gap
        }
      }
      gap = gap / 2
    }
    nums
  }
}

希尔排序PYTHON实现

def shell_sort(collection):
    gap = len(collection) // 2
    while (1 <= gap):
        for i in range(gap, len(collection)):
            j = i
            while (j >= 0 and collection[j - gap] > collection[j]):
                tmp = collection[j - gap] + collection[j]
                collection[j - gap] = tmp - collection[j - gap]
                collection[j] = tmp - collection[j - gap]
                j = j- gap
        gap = gap // 2
    return collection
if __name__=="__main__":

     print(shell_sort([2, 3, 8, 5, 4, 9]))

简单选择排序

选择排序(Selection sort)是一种简单直观的排序算法。

它的基本思想是：首先在未排序的数列中找到最小(or最大)元素，然后将其存放到数列的起始位置；接着，再从剩余未排序的元素中继续寻找最小(or最大)元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

下面以数列{20,40,30,10,60,50}为例，演示它的选择排序过程(如下图)：

第1趟：i=0。找出a[1...5]中的最小值a[3]=10，然后将a[0]和a[3]互换。 数列变化：20,40,30,10,60,50 -- > 10,40,30,20,60,50

第2趟：i=1。找出a[2...5]中的最小值a[3]=20，然后将a[1]和a[3]互换。 数列变化：10,40,30,20,60,50 -- > 10,20,30,40,60,50

第3趟：i=2。找出a[3...5]中的最小值，由于该最小值大于a[2]，该趟不做任何处理。 

第4趟：i=3。找出a[4...5]中的最小值，由于该最小值大于a[3]，该趟不做任何处理。 

第5趟：i=4。交换a[4]和a[5]的数据。 数列变化：10,20,30,40,60,50 -- > 10,20,30,40,50,60。

时间复杂度和稳定性

选择排序的时间复杂度是O(N2)。

假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢？N-1！因此，选择排序的时间复杂度是O(N2)。

选择排序是稳定的算法，它满足稳定算法的定义。

算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

选择排序JAVA实现

import java.util.Arrays;

import static javaTest.SortUtils.less;
import static javaTest.SortUtils.swap;

/**
 * ClassName SelectionSort.java
 * author Rhett.wang
 * version 1.0.0
 * Description TODO
 * createTime 2020年01月18日 17:10:00
 */
public class SelectionSort implements SortAlgorithm {
    public static void main(String[] args) {
        Integer[] arr = {4, 23, 6, 78, 1, 54, 231, 9, 12};
        SelectionSort sort = new SelectionSort();
        System.out.println(Arrays.toString(sort.sort(arr)));
    }
    /**
     * Main method arrays sorting algorithms
     *
     * @param unsorted - an array should be sorted
     * @return a sorted array
     */
    @Override
    public <T extends Comparable<T>> T[] sort(T[] unsorted) {
        int n=unsorted.length;
        for(int i=0;i<n-1;i++){
            int min =i;
            for(int j=i+1;j<n;j++){
                if(less(unsorted[j],unsorted[i])){
                   min=j;
                }
            }
            if(min != i){
                swap(unsorted,i,min);
            }
        }
        return unsorted;
    }
}

工具类SortUtils

/**
 * ClassName SortUtils.java
 * author Rhett.wang
 * version 1.0.0
 * Description TODO
 * createTime 2020年01月16日 17:49:00
 */
import java.util.Arrays;
import java.util.List;

/**
 * The class contains util methods
 *
 * @author Podshivalov Nikita (https://github.com/nikitap492)
 **/
final class SortUtils {

    /**
     * Helper method for swapping places in array
     *
     * @param array The array which elements we want to swap
     * @param idx   index of the first element
     * @param idy   index of the second element
     */
    static <T> boolean swap(T[] array, int idx, int idy) {
        T swap = array[idx];
        array[idx] = array[idy];
        array[idy] = swap;
        return true;
    }


    /**
     * This method checks if first element is less then the other element
     *
     * @param v first element
     * @param w second element
     * @return true if the first element is less then the second element
     */
    static <T extends Comparable<T>> boolean less(T v, T w) {
        return v.compareTo(w) < 0;
    }


    /**
     * Just print list
     *
     * @param toPrint - a list which should be printed
     */
    static void print(List<?> toPrint) {
        toPrint.stream()
                .map(Object::toString)
                .map(str -> str + " ")
                .forEach(System.out::print);

        System.out.println();
    }


    /**
     * Prints an array
     *
     * @param toPrint - the array  which should be printed
     */
    static void print(Object[] toPrint) {
        System.out.println(Arrays.toString(toPrint));
    }


    /**
     * Swaps all position from {@param left} to @{@param right} for {@param array}
     *
     * @param array is an array
     * @param left  is a left flip border of the array
     * @param right is a right flip border of the array
     */
    static <T extends Comparable<T>> void flip(T[] array, int left, int right) {
        while (left <= right) {
            swap(array, left++, right--);
        }
    }
}

 选择排序SCALA实现

/**
  * ClassName SelectionSort.java
  * author Rhett.wang
  * version 1.0.0
  * Description TODO
  * createTime 2020年01月18日 19:28:00
  */
object SelectionSort {
  def main(args: Array[String]) {
    var nums: Array[Int] = Array(2, 3, 8, 5, 4, 9)
    sort(nums)
    nums.foreach(x=>print(x))

  }
  def sort(nums:Array[Int]):Array[Int]={
    for(i <- 0 until nums.length){
      var min:Int=i
      var minVal=nums(i)
      for(j <- i+1 to nums.length-1){
        if(nums(j) < minVal){
          min = j
          minVal=nums(j)
        }
      }
      val temp :Int=nums(i)
      nums(i)=nums(min)
      nums(min)=temp
    }
    nums
  }

}

选择排序PYTHON实现

def selection_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr
if __name__=="__main__":

     print(selection_sort([2, 3, 8, 5, 4, 9, 2, 1]))

冒泡排序

冒泡排序(Bubble Sort)，又被称为气泡排序或泡沫排序。

它是一种较简单的排序算法。它会遍历若干 次要排序的数列，每次遍历时，它都会从前往后依次的比较相邻两个数的大小；如果前者比后者大，则交换它们的位置。这样，一次遍历之后，最大的元素就在数列 的末尾！ 采用相同的方法再次遍历时，第二大的元素就被排列在最大元素之前。重复此操作，直到整个数列都有序为止！

下面以数列{20,40,30,10,60,50}为例，演示它的冒泡排序过程(如下图)

当i=5,j=0时，a[0]<a[1]。此时，不做任何处理！

当i=5,j=1时，a[1]>a[2]。此时，交换a[1]和a[2]的值；交换之后，a[1]=30，a[2]=40。

当i=5,j=2时，a[2]>a[3]。此时，交换a[2]和a[3]的值；交换之后，a[2]=10，a[3]=40。

当i=5,j=3时，a[3]<a[4]。此时，不做任何处理！

当i=5,j=4时，a[4]>a[5]。此时，交换a[4]和a[5]的值；交换之后，a[4]=50，a[3]=60。

于是，第1趟排序完之后，数列{20,40,30,10,60,50}变成了{20,30,10,40,50,60}。此时，数列末尾的值最大。

时间复杂度和稳定性

冒泡排序的时间复杂度是O(N2)。

假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢？N-1次！因此，冒泡排序的时间复杂度是O(N2)。

冒泡排序是稳定的算法，它满足稳定算法的定义。

算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

冒泡排序JAVA实现

import java.util.Arrays;

import static javaTest.SortUtils.less;
import static javaTest.SortUtils.swap;

/**
 * ClassName BubbleSort.java
 * author Rhett.wang
 * version 1.0.0
 * Description TODO
 * createTime 2020年01月18日 20:06:00
 */
class BubbleSort implements SortAlgorithm {
    /**
     * This method implements the Generic Bubble Sort
     *
     * @param array The array to be sorted
     *              Sorts the array in increasing order
     **/

    @Override
    public <T extends Comparable<T>> T[] sort(T[] array) {
        for (int i = 0, size = array.length; i < size - 1; ++i) {
            boolean swapped = false;
            for (int j = 0; j < size - 1 - i; ++j) {
                if (less(array[j], array[j + 1])) {
                    swap(array, j, j + 1);
                    swapped = true;
                }
            }
            if (!swapped) {
                break;
            }
        }
        return array;
    }

    // Driver Program
    public static void main(String[] args) {

        // Integer Input
        Integer[] integers = {4, 23, 6, 78, 1, 54, 231, 9, 12};
        BubbleSort bubbleSort = new BubbleSort();
        bubbleSort.sort(integers);

        // Output => 231, 78, 54, 23, 12, 9, 6, 4, 1
        System.out.println(Arrays.toString(integers));


        // String Input
        String[] strings = {"c", "a", "e", "b", "d"};
        //Output => e, d, c, b, a
        System.out.println(Arrays.toString(strings));
    }
}

冒泡排序SCALA实现

import util.control.Breaks._
/**
  * ClassName BubbleSort.java
  * author Rhett.wang
  * version 1.0.0
  * Description TODO
  * createTime 2020年01月18日 20:23:00
  */
object BubbleSort {
  def main(args: Array[String]) {
    var nums: Array[Int] = Array(2, 3, 8, 5, 4, 9)
    bubbleSort(nums)
    nums.foreach(x=>print(x))
  }

  def bubbleSort(array: Array[Int]) :  Array[Int] = {
    breakable {
      for (i <- 0 to array.length - 1) {
        var swap = false

        for (j <- 0 to array.length - 2) {
          if (array(j) > array(j + 1)) {
            val temp = array(j)
            array(j) = array(j + 1)
            array(j + 1) = temp
            swap = true
          }
        }

        if (!swap) {
          break
        }
      }
    }
    array
  }
}

冒泡排序PYTHON实现

def bubble_sort(collection):
    length = len(collection)
    for i in range(length - 1):
        swapped = False
        for j in range(length - 1 - i):
            if collection[j] > collection[j + 1]:
                swapped = True
                collection[j], collection[j + 1] = collection[j + 1], collection[j]
        if not swapped:
            break  # Stop iteration if the collection is sorted.
    return collection
if __name__=="__main__":

     print(bubble_sort([2, 3, 8, 5, 4, 9, 2, 1]))

快速排序

快速排序(Quick Sort)使用分治法策略。

它的基本思想是：选择一个基准数，通过一趟排序将要排序的数据分割成独立的两部分；其中一部分的所有数据都比另外一部分的所有数据都要小。然后，再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

排序流程：

从数列中挑出一个基准值。

将所有比基准值小的摆放在基准前面，所有比基准值大的摆在基准的后面(相同的数可以到任一边)；在这个分区退出之后，该基准就处于数列的中间位置。

递归地把"基准值前面的子数列"和"基准值后面的子数列"进行排序

下面以数列a={30,40,60,10,20,50}为例，演示它的快速排序过程(如下图)：

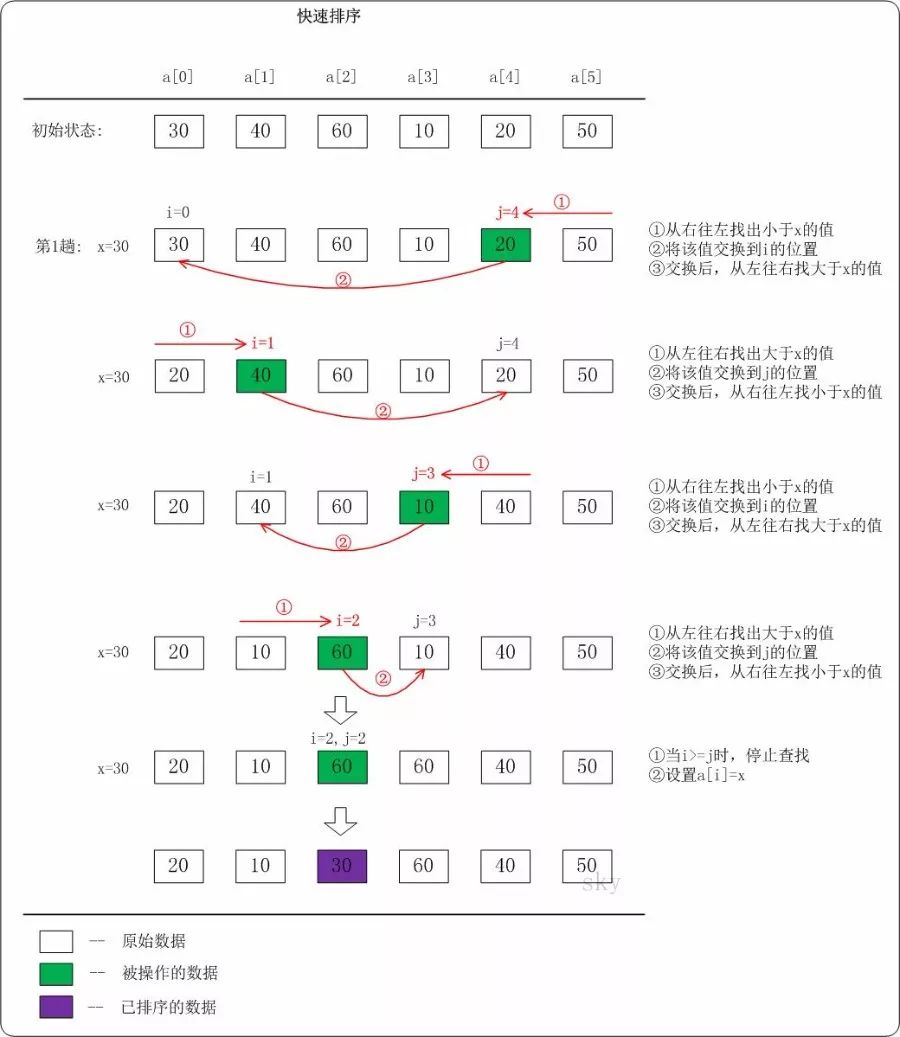
上图只是给出了第1趟快速排序的流程。在第1趟中，设置x=a[i]，即x=30。

从"右 --> 左"查找小于x的数：找到满足条件的数a[j]=20，此时j=4；然后将a[j]赋值a[i]，此时i=0；接着从左往右遍历。

从"左 --> 右"查找大于x的数：找到满足条件的数a[i]=40，此时i=1；然后将a[i]赋值a[j]，此时j=4；接着从右往左遍历。

从"右 --> 左"查找小于x的数：找到满足条件的数a[j]=10，此时j=3；然后将a[j]赋值a[i]，此时i=1；接着从左往右遍历。

从"左 --> 右"查找大于x的数：找到满足条件的数a[i]=60，此时i=2；然后将a[i]赋值a[j]，此时j=3；接着从右往左遍历。

从"右 --> 左"查找小于x的数：没有找到满足条件的数。当i>=j时，停止查找；然后将x赋值给a[i]。此趟遍历结束！

按照同样的方法，对子数列进行递归遍历。最后得到有序数组。

快速排序的时间复杂度和稳定性

快速排序稳定性

快速排序是不稳定的算法，它不满足稳定算法的定义。

算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

快速排序时间复杂度

快速排序的时间复杂度在最坏情况下是O(N2)，平均的时间复杂度是O(N*lgN)。

这句话很好理解：假设被排序的数列中有N个数。遍历一次的时间复杂度是O(N)，需要遍历多少次呢？至少lg(N+1)次，最多N次。

(01) 为什么最少是lg(N+1)次？快速排序是采用的分治法进行遍历的，我们将它看作一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的定义，它的深度至少是lg(N+1)。因此，快速排序的遍历次数最少是lg(N+1)次。

(02) 为什么最多是N次？这个应该非常简单，还是将快速排序看作一棵二叉树，它的深度最大是N。因此，快读排序的遍历次数最多是N次。

快速排序JAVA实现

import static Sorts.SortUtils.*;

/**
 * @author Varun Upadhyay (https://github.com/varunu28)
 * @author Podshivalov Nikita (https://github.com/nikitap492)
 * @see SortAlgorithm
 */
class QuickSort implements SortAlgorithm {

    /**
     * This method implements the Generic Quick Sort
     *
     * @param array The array to be sorted
     *              Sorts the array in increasing order
     **/

    @Override
    public <T extends Comparable<T>> T[] sort(T[] array) {
        doSort(array, 0, array.length - 1);
        return array;
    }


    /**
     * The sorting process
     *
     * @param left  The first index of an array
     * @param right The last index of an array
     * @param array The array to be sorted
     **/

    private static <T extends Comparable<T>> void doSort(T[] array, int left, int right) {
        if (left < right) {
            int pivot = randomPartition(array, left, right);
            doSort(array, left, pivot - 1);
            doSort(array, pivot, right);
        }
    }

    /**
     * Ramdomize the array to avoid the basically ordered sequences
     * 
     * @param array The array to be sorted
     * @param left  The first index of an array
     * @param right The last index of an array
     * @return the partition index of the array
     */

    private static <T extends Comparable<T>> int randomPartition(T[] array, int left, int right) {
        int randomIndex = left + (int)(Math.random()*(right - left + 1));
        swap(array, randomIndex, right);
        return partition(array, left, right);
    }

    /**
     * This method finds the partition index for an array
     *
     * @param array The array to be sorted
     * @param left  The first index of an array
     * @param right The last index of an array
     *              Finds the partition index of an array
     **/

    private static <T extends Comparable<T>> int partition(T[] array, int left, int right) {
        int mid = (left + right) / 2;
        T pivot = array[mid];

        while (left <= right) {
            while (less(array[left], pivot)) {
                ++left;
            }
            while (less(pivot, array[right])) {
                --right;
            }
            if (left <= right) {
                swap(array, left, right);
                ++left;
                --right;
            }
        }
        return left;
    }

    // Driver Program
    public static void main(String[] args) {

        // For integer input
        Integer[] array = {3, 4, 1, 32, 0, 1, 5, 12, 2, 5, 7, 8, 9, 2, 44, 111, 5};

        QuickSort quickSort = new QuickSort();
        quickSort.sort(array);

        //Output => 0 1 1 2 2 3 4 5 5 5 7 8 9 12 32 44 111
        print(array);

        String[] stringArray = {"c", "a", "e", "b", "d"};
        quickSort.sort(stringArray);

        //Output => a    b    c    d    e
        print(stringArray);
    }
}

快速排序SCALA实现

object QuickSort {
  /**
    *
    * @param array - a sequence of unsorted integers
    * @return - sequence of sorted integers @array
    */

  def quickSort(array: Array[Int]): Array[Int] = {

    def quickSortImpl(array: Array[Int], first: Int, last: Int): Array[Int] = {
      var pivot: Int = 0
      var i: Int = 0
      var j: Int = 0
      var temp: Int = 0

      if (first < last) {
        pivot = first
        i = first
        j = last

        while (i < j) {
          while (array(i) <= array(pivot) && i < last) {
            i += 1
          }

          while (array(j) > array(pivot)) {
            j -= 1
          }

          if (i < j) {
            temp = array(i)
            array(i) = array(j)
            array(j) = temp
          }
        }

        temp = array(pivot)
        array(pivot) = array(j)
        array(j) = temp
        quickSortImpl(array, first, j - 1)
        quickSortImpl(array, j + 1, last)
      }

      array
    }

    quickSortImpl(array,0, array.length-1)
  }
}

快速排序PYTHON实现

def quick_sort_3partition(sorting, left, right):
    if right <= left:
        return
    a = i = left
    b = right
    pivot = sorting[left]
    while i <= b:
        if sorting[i] < pivot:
            sorting[a], sorting[i] = sorting[i], sorting[a]
            a += 1
            i += 1
        elif sorting[i] > pivot:
            sorting[b], sorting[i] = sorting[i], sorting[b]
            b -= 1
        else:
            i += 1
    quick_sort_3partition(sorting, left, a - 1)
    quick_sort_3partition(sorting, b + 1, right)


if __name__ == "__main__":
    user_input = input("Enter numbers separated by a comma:\n").strip()
    unsorted = [int(item) for item in user_input.split(",")]
    quick_sort_3partition(unsorted, 0, len(unsorted) - 1)
    print(unsorted)

归并排序

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分 治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶 段得到的各答案"修补"在一起，即分而治之)。

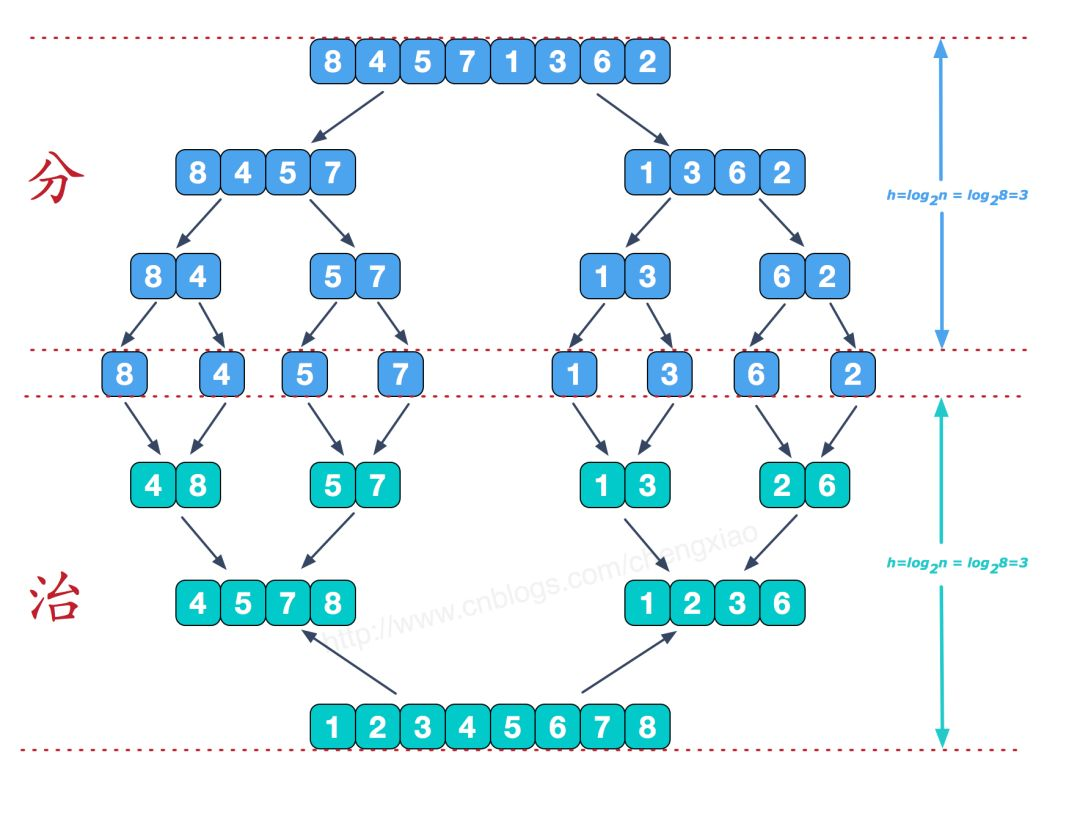
 可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

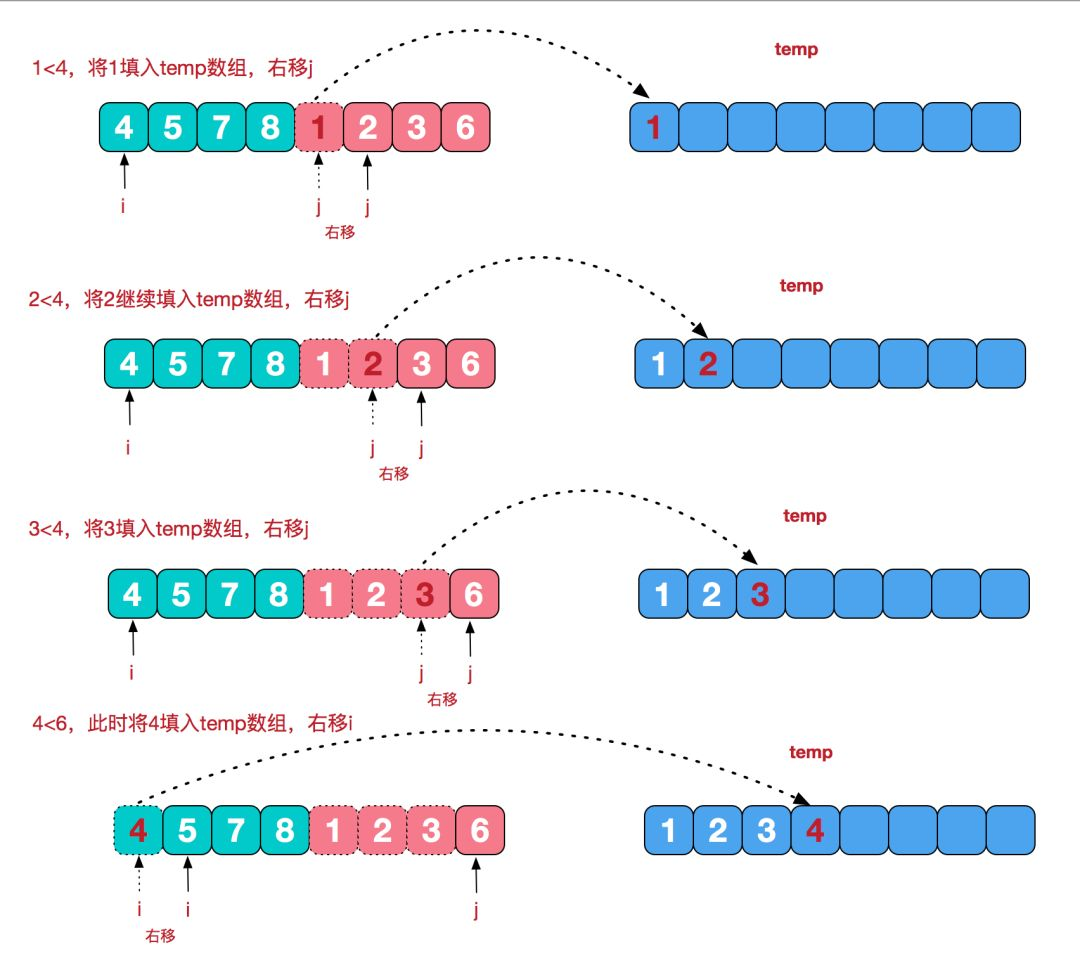
合并相邻有序子序列

再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

归并排序JAVA实现

import static Sorts.SortUtils.print;

/**
 * This method implements the Generic Merge Sort
 *
 * @author Varun Upadhyay (https://github.com/varunu28)
 * @author Podshivalov Nikita (https://github.com/nikitap492)
 * @see SortAlgorithm
 */

class MergeSort implements SortAlgorithm {

    /**
     * This method implements the Generic Merge Sort
     *
     * @param unsorted the array which should be sorted
     * @param <T>      Comparable class
     * @return sorted array
     */
    @Override
    @SuppressWarnings("unchecked")
    public <T extends Comparable<T>> T[] sort(T[] unsorted) {
        doSort(unsorted, 0, unsorted.length - 1);
        return unsorted;
    }

    /**
     * @param arr   The array to be sorted
     * @param left  The first index of the array
     * @param right The last index of the array
     *              Recursively sorts the array in increasing order
     **/
    private static <T extends Comparable<T>> void doSort(T[] arr, int left, int right) {
        if (left < right) {
            int mid = left + (right - left) / 2;
            doSort(arr, left, mid);
            doSort(arr, mid + 1, right);
            merge(arr, left, mid, right);
        }

    }

    /**
     * This method implements the merge step of the merge sort
     *
     * @param arr   The array to be sorted
     * @param left  The first index of the array
     * @param mid   The middle index of the array
     * @param right The last index of the array
     *              merges two parts of an array in increasing order
     **/

    private static <T extends Comparable<T>> void merge(T[] arr, int left, int mid, int right) {
        int length = right - left + 1;
        T[] temp = (T[]) new Comparable[length];
        int i = left;
        int j = mid + 1;
        int k = 0;

        while (i <= mid && j <= right) {
            if (arr[i].compareTo(arr[j]) <= 0) {
                temp[k++] = arr[i++];
            } else {
                temp[k++] = arr[j++];
            }
        }

        while (i <= mid) {
            temp[k++] = arr[i++];
        }

        while (j <= right) {
            temp[k++] = arr[j++];
        }

        System.arraycopy(temp, 0, arr, left, length);
    }

    // Driver program
    public static void main(String[] args) {

        // Integer Input
        Integer[] arr = {4, 23, 6, 78, 1, 54, 231, 9, 12};
        MergeSort mergeSort = new MergeSort();
        mergeSort.sort(arr);

        // Output => 1       4       6    9    12    23    54    78    231
        print(arr);

        // String Inpu
        String[] stringArray = {"c", "a", "e", "b", "d"};
        mergeSort.sort(stringArray);
        //Output => a    b    c    d    e
        print(stringArray);
    }
}

归并排序SCALA实现

object MergeSort {

  /**
    *
    * @param array   - a sequence of unsorted integers
    * @return - sequence of sorted integers @array
    */

  def mergeSort(array: Array[Int]): Array[Int] = {

    def sort(array: Array[Int]): Array[Int] = {
      MS(array, 0, array.length - 1)
    }

    def MS(array: Array[Int], low: Int, high: Int): Array[Int] = {
      if (low < high) {
        val mid = (low + high) / 2
        MS(array, low, mid)
        MS(array, mid + 1, high)
        merge(array, low, mid, high)
      } else {
        array
      }
    }

    def merge(array: Array[Int], low: Int, mid: Int, high: Int): Array[Int] = {
      // copy subarrays
      val left = array.slice(low, mid + 1)
      val right = array.slice(mid + 1, high + 1)

      var i = 0
      var j = 0
      var k = low
      while (k < high + 1) {
        // must check if empty to avoid exceptions
        if (i > left.length - 1) {
          array(k) = right(j)
          j = j + 1
        } else if (j > right.length - 1) {
          array(k) = left(i)
          i = i + 1
        } else if (left(i) <= right(j)) {
          array(k) = left(i)
          i = i + 1
        } else {
          array(k) = right(j)
          j = j + 1
        }
        k = k + 1
      }

      array

    }

    sort(array)
  }

}

归并排序PYTHON实现

def merge_sort(collection):
    """Pure implementation of the merge sort algorithm in Python
    :param collection: some mutable ordered collection with heterogeneous
    comparable items inside
    :return: the same collection ordered by ascending
    Examples:
    >>> merge_sort([0, 5, 3, 2, 2])
    [0, 2, 2, 3, 5]
    >>> merge_sort([])
    []
    >>> merge_sort([-2, -5, -45])
    [-45, -5, -2]
    """

    def merge(left, right):
        """merge left and right
        :param left: left collection
        :param right: right collection
        :return: merge result
        """
        result = []
        while left and right:
            result.append((left if left[0] <= right[0] else right).pop(0))
        return result + left + right

    if len(collection) <= 1:
        return collection
    mid = len(collection) // 2
    return merge(merge_sort(collection[:mid]), merge_sort(collection[mid:]))


if __name__ == "__main__":
    user_input = input("Enter numbers separated by a comma:\n").strip()
    unsorted = [int(item) for item in user_input.split(",")]
    print(*merge_sort(unsorted), sep=",")

堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。

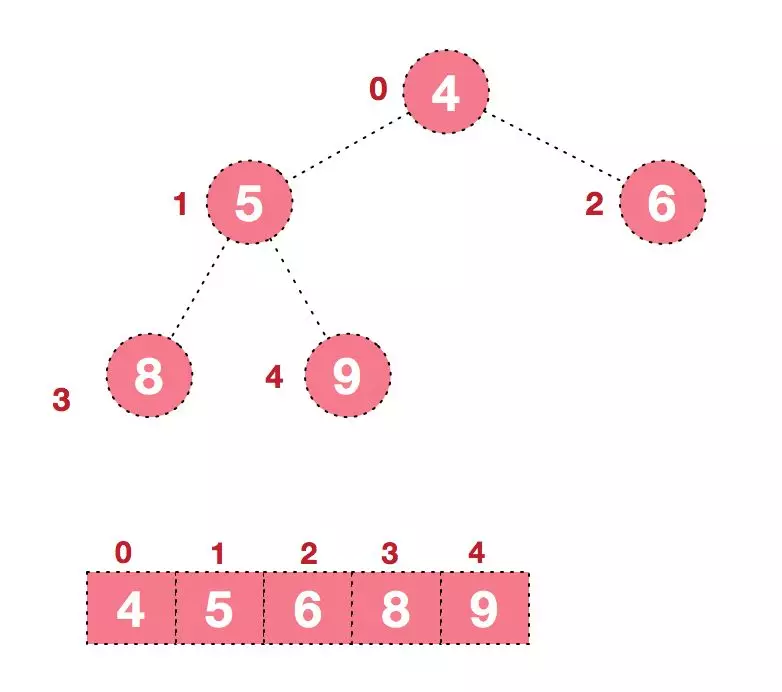
堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

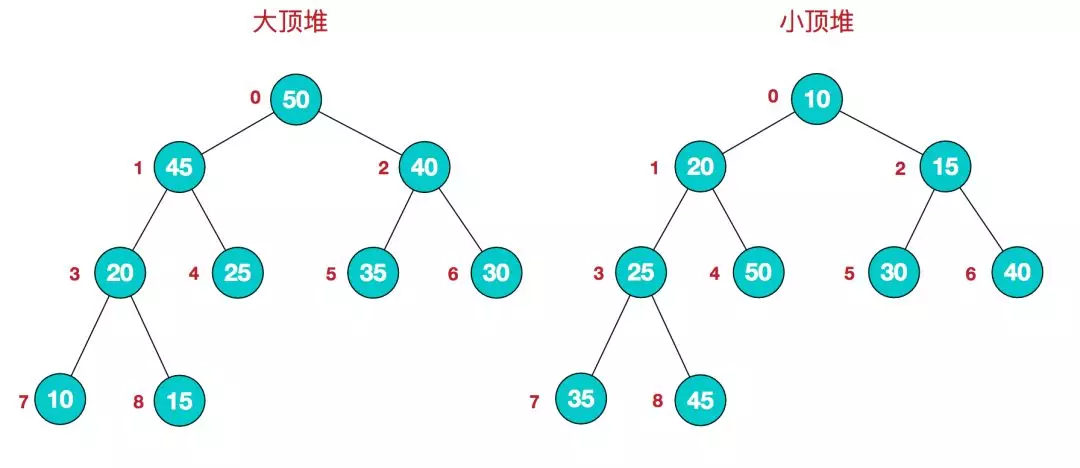
 同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子：

 该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]  

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]  

堆排序基本思想及步骤

 堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)：

1.假设给定无序序列结构如下：

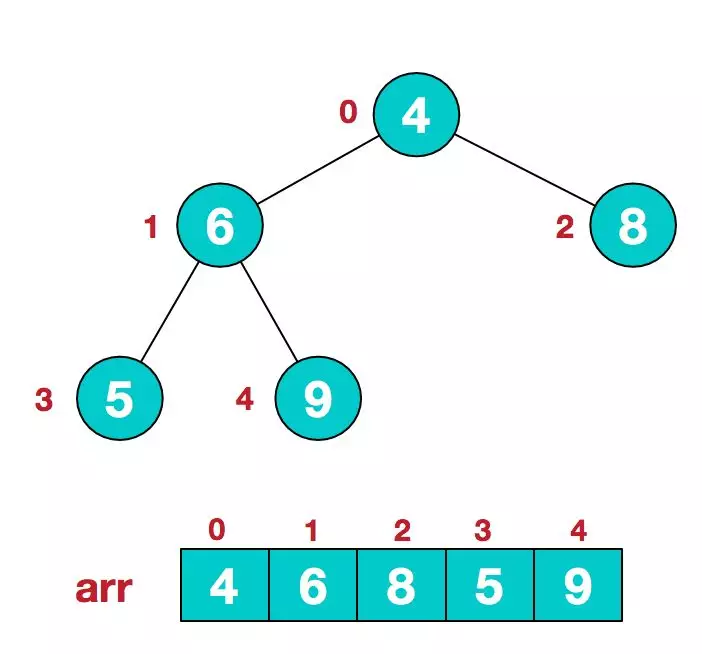
 2.此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

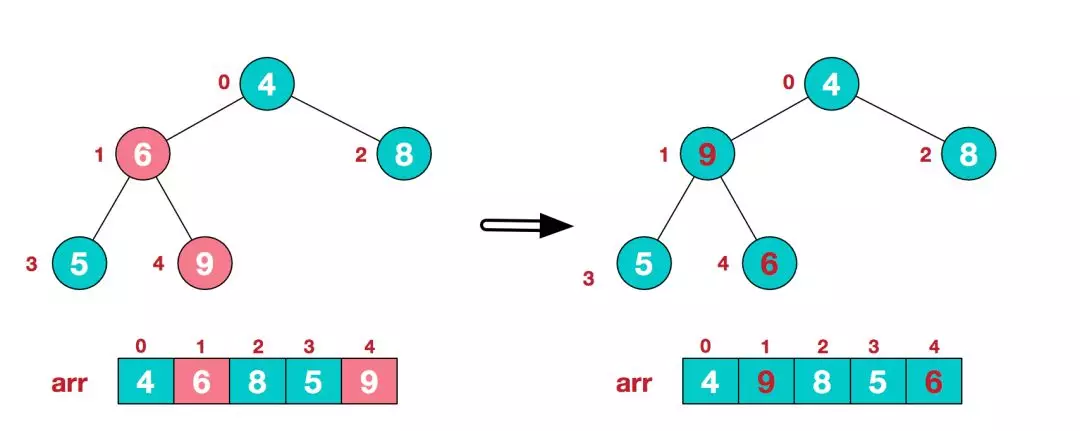
 3.找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

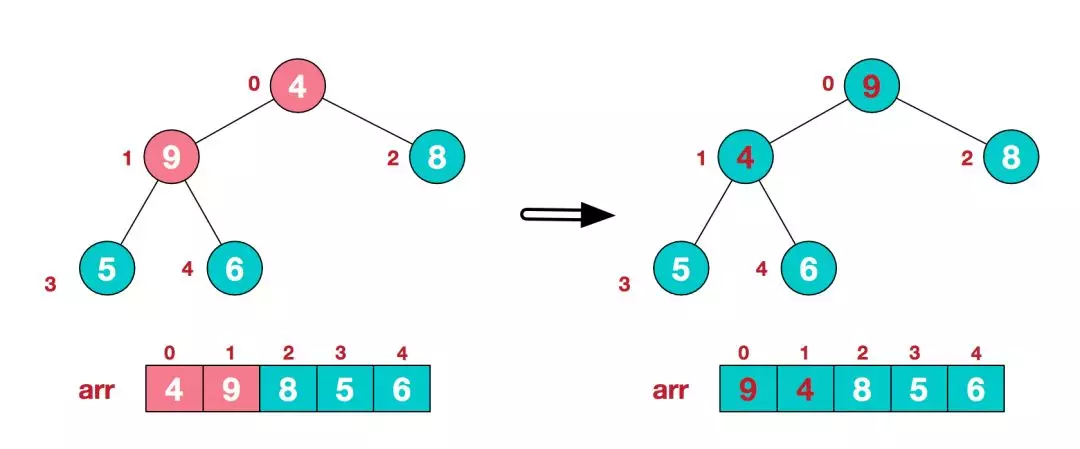
这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

 

此时，我们就将一个无需序列构造成了一个大顶堆。

步骤二 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

a.将堆顶元素9和末尾元素4进行交换。

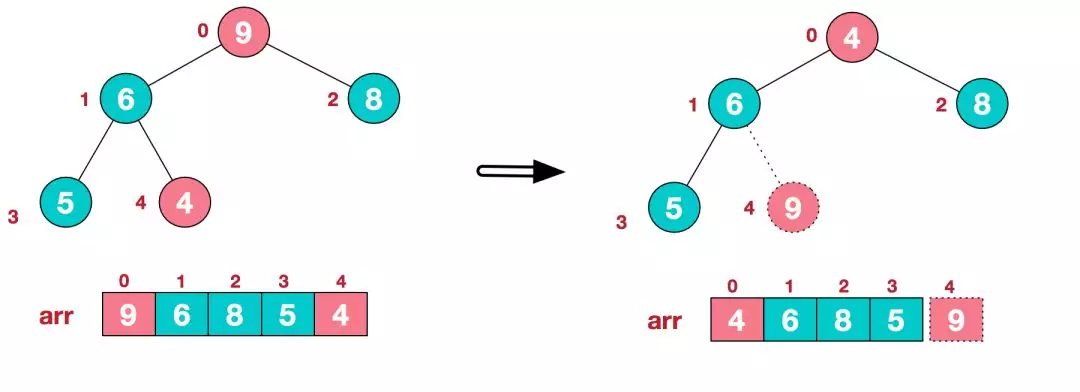
b.重新调整结构，使其继续满足堆定义

 

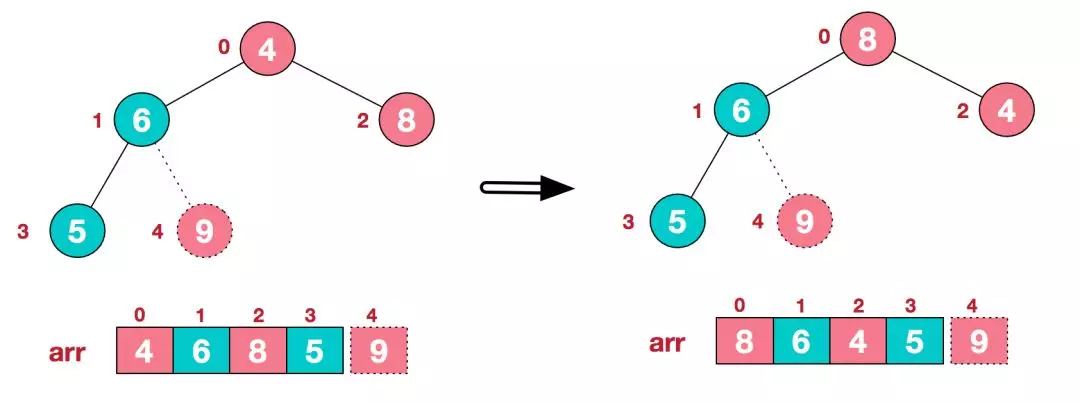
c.再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.

 

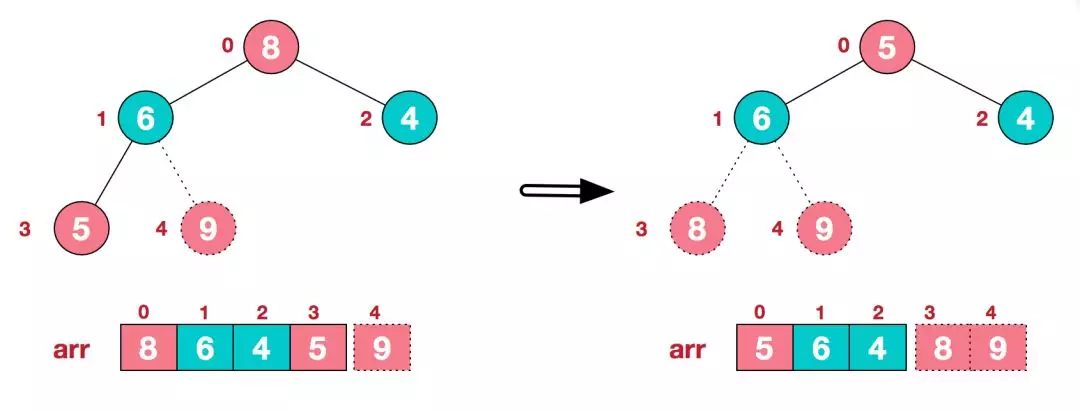
 后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

再简单总结下堆排序的基本思路：

将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

堆排序是一种选择排序，整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n)，在交换并重建堆的过程中，需交换n-1次，而重建堆的过程中，根据完全二叉树的性质，[log2(n-1),log2(n-2)...1]逐步递减，近似为nlogn。所以堆排序时间复杂度一般认为就是O(nlogn)级。

堆排序JAVA实现

package javaTest;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

import static javaTest.SortUtils.less;
import static javaTest.SortUtils.swap;
import static javafx.scene.input.KeyCode.T;

/**
 * ClassName HeapSort.java
 * author Rhett.wang
 * version 1.0.0
 * Description TODO
 * createTime 2020年02月06日 09:19:00
 */
public class HeapSort implements SortAlgorithm {
    public static void main(String[] args) {
        Integer[] heap = {4, 23, 6, 78, 1, 54, 231, 9, 12};
        HeapSort heapSort = new HeapSort();
        System.out.println(heapSort.sort(heap));
    }
    /**
     * Main method arrays sorting algorithms
     *
     * @param unsorted - an array should be sorted
     * @return a sorted array
     */
    @Override
    public <T extends Comparable<T>> T[] sort(T[] unsorted) {
        return sort(Arrays.asList(unsorted)).toArray(unsorted);
    }
    @Override
    public <T extends Comparable<T>> List<T> sort(List<T> unsorted){
        int size = unsorted.size();
        Heap<T> heap=new Heap<>(unsorted.toArray((T[]) new Comparable[unsorted.size()]));
        heap.makeMinHeap(0);
        List<T> sorted=new ArrayList<>(size);
        while(size>0){
            T min =heap.getRoot(--size);
            sorted.add(min);
        }
        return sorted;
    }
    private static class Heap<T extends Comparable<T>>{
        private T[] heap;
        public Heap(T[] heap){
            this.heap=heap;
        }
        public T getRoot(int size){
            swap(heap,0,size);
            heapSubtree(0,size-1);
            return heap[size];
        }
        private void heapSubtree(int rootIndex,int lastChild){
            int leftIndex=rootIndex*2 +1;
            int rightIndex=rootIndex*2 +2;
            T root =heap[rootIndex];
            if(rightIndex<=lastChild){
                T left=heap[leftIndex];
                T right=heap[rightIndex];
                if(less(left,right) && less(left,root)){
                    swap(heap,leftIndex,rootIndex);
                    heapSubtree(leftIndex,lastChild);
                }else if(less(right,root)){
                    swap(heap,rightIndex,rootIndex);
                    heapSubtree(rightIndex,lastChild);
                }
            }else if(leftIndex<=lastChild){
                T left=heap[leftIndex];
                if(less(left,root)){
                    swap(heap,leftIndex,rootIndex);
                    heapSubtree(leftIndex,lastChild);
                }
            }
        }
        private void makeMinHeap(int root){
            int leftIndex=root*2+1;
            int rightIndex=root*2+2;
            boolean hasLeftChild=leftIndex<heap.length;
            boolean hasRightChild=rightIndex<heap.length;

            if(hasRightChild){
                makeMinHeap(leftIndex);
                makeMinHeap(rightIndex);
                heapSubtree(root,heap.length-1);
            }else if(hasLeftChild){
                heapSubtree(root,heap.length-1);
            }
        }

    }
}

java第二种方式实现

package javaTest;

import java.util.Arrays;

/**
 * ClassName HeapSort1.java
 * author Rhett.wang
 * version 1.0.0
 * Description TODO
 * createTime 2020年02月06日 10:57:00
 */
public class HeapSort1 {
    public static void main(String[] args) {
        int []arr = {9,8,7,6,5,4,3,2,1};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
    public static void swap(int[] arr,int a,int b){
        int temp=arr[a];
        arr[a]=arr[b];
        arr[b]=temp;
    }
    public static void adjustHeap(int[] arr,int i,int length){
        int temp=arr[i];
        for(int k=i*2+1;k<length;k=k*2+1){
            if(k+1<length && arr[k]<arr[k+1]){
                k++;
            }
            if(arr[k]>temp){
                arr[i]=arr[k];
                i=k;
            }else{
                break;
            }
        }
        arr[i]=temp;
    }
    public static void sort(int[] arr){
        for(int i=arr.length/2-1;i>=0;i--){
            adjustHeap(arr,i,arr.length);
        }
        for(int j=arr.length-1;j>0;j--){
            swap(arr,0,j);
            adjustHeap(arr,0,j);
        }
    }
}

堆排序SCALA实现

package scala

/**
  * ClassName HeapSort1.java
  * author Rhett.wang
  * version 1.0.0
  * Description TODO
  * createTime 2020年02月05日 10:27:00
  */
object HeapSort1 {
  def main(args: Array[String]) {
     println(heapsort(Array(8,3,2,4,1,9,7,19,18,14,15)).toList)
  }
  def heapsort(arr:Array[Int]):Array[Int]={

    val sortedArray=arr.clone()
    def sift(start:Int,count:Int): Unit ={
      var root=start

      while(root*2+1<count){
        var child =root*2+1
        if(child<count-1 &&sortedArray(child)<sortedArray(child+1)){
          child +=1
        }
        if(sortedArray(root)<sortedArray(child)){
          val t=sortedArray(root)
          sortedArray(root)=sortedArray(child)
          sortedArray(child)=t
          root=child
        }else return
      }
    }
    var count=sortedArray.length
    var start=count/2-1
    var end=count-1
    while(start>=0){
      sift(start,count)
      start -=1
    }
    println(sortedArray.toList)
    while(end>0){
      val t=sortedArray(end)
      sortedArray(end)=sortedArray(0)
      sortedArray(0)=t
      sift(0,end)
      end -=1
    }

    sortedArray
  }

}

堆排序PYTHON实现

def heapif(unsorted,index,heap_size):
    largest=index
    left_index = 2*index +1
    right_index=2*index + 2
    if left_index < heap_size and unsorted[left_index] >unsorted[largest]:
        largest = left_index
    if right_index < heap_size and unsorted[right_index] > unsorted[largest]:
        largest=right_index

    if largest != index:
        unsorted[largest] , unsorted[index] = unsorted[index],unsorted[largest]
        heapif(unsorted,largest,heap_size)

def heap_sort(unsorted):
    n =len(unsorted)
    for i in range(n//2-1,-1,-1):
        heapif(unsorted,i,n)
    for i in range(n-1,0,-1):
        unsorted[0],unsorted[i] =unsorted[i],unsorted[0]
        heapif(unsorted,0,i)

    return unsorted

if __name__ == "__main__":
    unsorted =[9,5,8,3,2,7]
    test = heap_sort(unsorted)
    print(test)

基数排序

基数排序与本系列前面讲解的七种排序方法都不同，它不需要比较关键字的大小。

它是根据关键字中各位的值，通过对排序的N个元素进行若干趟“分配”与“收集”来实现排序的。 

不妨通过一个具体的实例来展示一下，基数排序是如何进行的。 设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}。

我们知道，任何一个阿拉伯数，它的各个位数上的基数都是以0~9来表示的。所以我们不妨把0~9视为10个桶。 

我们先根据序列的个位数的数字来进行分类，将其分到指定的桶中。例如：R[0] = 50，个位数上是0，将这个数存入编号为0的桶中。

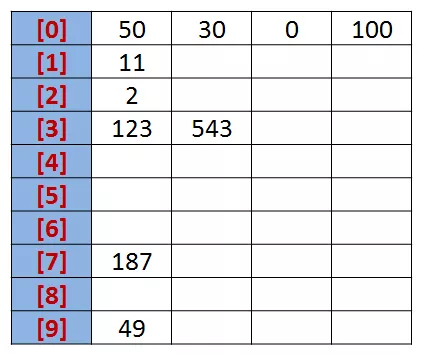
分类后，我们在从各个桶中，将这些数按照从编号0到编号9的顺序依次将所有数取出来。这时，得到的序列就是个位数上呈递增趋势的序列。 

按照个位数排序： {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}。接下来，可以对十位数、百位数也按照这种方法进行排序，最后就能得到排序完成的序列。

算法分析

时间复杂度

通过上文可知，假设在基数排序中，r为基数，d为位数。则基数排序的时间复杂度为O(d(n+r))。我们可以看出，基数排序的效率和初始序列是否有序没有关联。

空间复杂度

在基数排序过程中，对于任何位数上的基数进行“装桶”操作时，都需要n+r个临时空间。

算法稳定性

在基数排序过程中，每次都是将当前位数上相同数值的元素统一“装桶”，并不需要交换位置。所以基数排序是稳定的算法。

基数排序JAVA实现

package notes.javase.algorithm.sort;
public class RadixSort {
   // 获取x这个数的d位数上的数字
   // 比如获取123的1位数，结果返回3
   public int getDigit(int x, int d) {
       int a[] = {
               1, 1, 10, 100
       }; // 本实例中的最大数是百位数，所以只要到100就可以了
       return ((x / a[d]) % 10);
   }

   public void radixSort(int[] list, int begin, int end, int digit) {
       final int radix = 10; // 基数
       int i = 0, j = 0;
       int[] count = new int[radix]; // 存放各个桶的数据统计个数
       int[] bucket = new int[end - begin + 1];
       // 按照从低位到高位的顺序执行排序过程
       for (int d = 1; d <= digit; d++) {
           // 置空各个桶的数据统计
           for (i = 0; i < radix; i++) {
               count[i] = 0;
           }
           // 统计各个桶将要装入的数据个数
           for (i = begin; i <= end; i++) {
               j = getDigit(list[i], d);
               count[j]++;
           }

           // count[i]表示第i个桶的右边界索引
           for (i = 1; i < radix; i++) {
               count[i] = count[i] + count[i - 1];
           }

           // 将数据依次装入桶中
           // 这里要从右向左扫描，保证排序稳定性
           for (i = end; i >= begin; i--) {
               j = getDigit(list[i], d); 
               // 求出关键码的第k位的数字， 例如：576的第3位是5
               bucket[count[j] - 1] = list[i]; 
               // 放入对应的桶中，count[j]-1是第j个桶的右边界索引
               count[j]--; // 对应桶的装入数据索引减一
           }
           // 将已分配好的桶中数据再倒出来，此时已是对应当前位数有序的表
           for (i = begin, j = 0; i <= end; i++, j++) {
               list[i] = bucket[j];
           }
       }
   }

   public int[] sort(int[] list) {
       radixSort(list, 0, list.length - 1, 3);
       return list;
   }

   // 打印完整序列
   public void printAll(int[] list) {
       for (int value : list) {
           System.out.print(value + "\t");
       }
       System.out.println();
   }

   public static void main(String[] args) {
       int[] array = {
               50, 123, 543, 187, 49, 30, 0, 2, 11, 100
       };
       RadixSort radix = new RadixSort();
       System.out.print("排序前:\t\t");
       radix.printAll(array);
       radix.sort(array);
       System.out.print("排序后:\t\t");
       radix.printAll(array);
   }
}

基数排序PYTHON实现

def radix_sort(lst):
    RADIX = 10
    placement = 1

    # get the maximum number
    max_digit = max(lst)

    while placement < max_digit:
        # declare and initialize buckets
        buckets = [list() for _ in range(RADIX)]

        # split lst between lists
        for i in lst:
            tmp = int((i / placement) % RADIX)
            buckets[tmp].append(i)

        # empty lists into lst array
        a = 0
        for b in range(RADIX):
            buck = buckets[b]
            for i in buck:
                lst[a] = i
                a += 1

        # move to next
        placement *= RADIX

总结

感谢网络大神的分享：

https://github.com/TheAlgorithms/

https://mp.weixin.qq.com/s?__biz=MzAxNjk4ODE4OQ==&mid=2247487903&idx=3&sn=f482041f5b560ca85db9ad51c33f07f3&chksm=9bed30edac9ab9fbb523b1ce15e545d126e2b6a651951f8ea672d5f6d05809b9ae8f99d81411&mpshare=1&scene=1&srcid=0113MrSScIDzFwL6luR7bevY&sharer_sharetime=1579050754003&sharer_shareid=d40e8d2bb00008844e69867bcfc0d895#rd