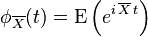柯西分布——正态分布的兄弟
观察变量分布时最重要的三个特性之一是胖-瘦(另两个是:单模-多模;对称-有偏),柯西分布和正态分布是极易混淆的分布曲线。
柯西分布也叫作柯西-洛伦兹分布,它是以奥古斯丁·路易·柯西与亨德里克·洛伦兹名字命名的连续概率分布,其概率密度函数为
其中x0是定义分布峰值位置的位置参数,γ是最大值一半处的一半宽度的尺度参数。
作为概率分布,通常叫作柯西分布,物理学家也将之称为洛伦兹分布或者Breit-Wigner分布。在物理学中的重要性很大一部分归因于它是描述受迫共振的微分方程的解。在光谱学中,它描述了被共振或者其它机制加宽的谱线形状。在下面的部分将使用柯西分布这个统计学术语。
x0 = 0且γ = 1的特例称为标准柯西分布,其概率密度函数为
特性
其累积分布函数为:
柯西分布的逆累积分布函数为
柯西分布的平均值、方差或者矩都没有定义,它的众数与中值有定义都等于 x0。
取 X 表示柯西分布随机变量,柯西分布的特性函数表示为:
如果 U 与 V 是期望值为 0、方差为 1 的两个独立正态分布随机变量的话,那么比值 U/V 为柯西分布。
标准柯西分布是学生t-分布自由度为1的特殊情况。
柯西分布是稳定分布:如果 ,则
,则 。
。
如果 X1, …, Xn 是分别符合柯西分布的相互独立同分布随机变量,那么算术平均数(X1 + … + Xn)/n 有同样的柯西分布。为了证明这一点,我们来计算采样平均的特性函数:
其中, 是采样平均值。这个例子表明不能舍弃中心极限定理中的有限变量假设。
是采样平均值。这个例子表明不能舍弃中心极限定理中的有限变量假设。
洛仑兹线性分布更适合于那种比较扁、宽的曲线 高斯线性分布则适合较高、较窄的曲线 当然,如果是比较居中的情况,两者都可以。 很多情况下,采用的是两者各占一定比例的做法。如洛伦茨占60%,高斯占40%.
概率密度函数 绿线是标准柯西分布 |
|
累积分布函数 与上图中的颜色对应 |
|
| 参数 |  位置参数(实数) 位置参数(实数) 尺度参数(实数) 尺度参数(实数) |
|---|---|
| 值域 |  |
| 概率密度函数 | ![柯西分布——正态分布的兄弟 \frac{1}{\pi\gamma\,\left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} \!](http://upload.wikimedia.org/math/1/1/0/110abf1f3bbdd637b6ddd41296caa067.png) |
| 累积分布函数 |  |
| 标记 | {{{notation}}} |
| 期望值 | (没有定义) |
| 中位数 |  |
| 众数 |  |
| 方差 | (没有定义) |
| 偏态 | (没有定义) |
| 峰态 | (没有定义) |
| 熵值 |  |
| 动差生成函数 | (没有定义) |
| 特征函数 | 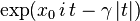 |


![柯西分布——正态分布的兄弟 f(x; x_0,\gamma) = \frac{1}{\pi\gamma \left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} \!](http://upload.wikimedia.org/math/9/9/3/99356e5bb7fb2597cb8c0c1f6436d764.png)
![柯西分布——正态分布的兄弟 = { 1 \over \pi } \left[ { \gamma \over (x - x_0)^2 + \gamma^2 } \right] \!](http://upload.wikimedia.org/math/8/9/7/897155389ea99bdf6d8e53432ff9a9fd.png)