代码随想录算法训练营第40天|647. 回文子串、516.最长回文子序列

LeetCode647

2025-03-14 17:51:23 星期五

题目描述：力扣647
文档讲解：代码随想录(programmercarl)647. 回文子串
视频讲解：《代码随想录》算法视频公开课：动态规划，字符串性质决定了DP数组的定义 | LeetCode：647.回文子串

代码随想录视频内容简记

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

这个题用动态规划的思路就是先要确定一点他是如何进行递推的？就是如果一个字符串从i到j，他的第i位和第j为是相同的，并且他的[i + 1, j - 1]部分是一个回文串，那么可以确定这个[i,j]的字符串也是一个回文串

[i...i+1........j-1...j]

梳理

1. 确定dp数组的含义，dp[i][j]表示一个从i开始到j结束的字符串是一个回文字符串，这里用true表示，注意不是回文串的数量了，这个数量关系没法递推

2. 确定递推公式，如果s[i] == s[j]，那么这个可以分成三种情况

   i == j只有一位，比如"a"，那么就是一个回文串

   j - i == 1表示两位，比如"aa"，也是一个回文串

   j - i > 1的表示两位以上，这时候就需要，if (dp[i + 1, j - 1] == true) dp[i, j] = true;

   剩下的s[i]和s[j]不相等的情况不用管，直接跳过就行。

3. 初始化dp数组，直接全部赋成false，所以上面的递推部分不用单独进行操作

4. 确定遍历顺序，可以看出，dp[i][j]是从dp[i + 1][j - 1]，也就是左下角推导而来的

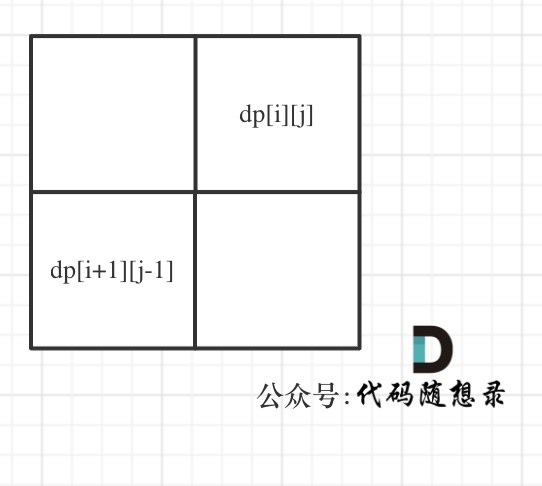
5. 打印dp数组

LeetCode测试

注意这里就是在写的时候，for循环的j的初始化语句需要j = i，因为dp数组的定义就是[i,j]，所以j需要比i大

点击查看代码

class Solution {
public:
    int countSubstrings(string s) {
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
        int result = 0;
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i; j < s.size(); j++) {
                if (s[i] == s[j]) {
                    if (j - i <= 1) {
                        dp[i][j] = true;
                        result++;
                    }
                    else if (dp[i + 1][j - 1] == true) {
                        dp[i][j] = true; 
                        result++;
                    }
                } 
            }
        }
        return result;
    }
};

LeetCode516

题目描述：力扣516
文档讲解：代码随想录(programmercarl)516.最长回文子序列
视频讲解：《代码随想录》算法视频公开课：动态规划再显神通，LeetCode：516.最长回文子序列

代码随想录视频内容简记

这个题感觉还是有点不太好操作的，和647有相通的地方，但是不多。感觉整体还是偏特殊一点

梳理

1. 确定dp[i][j]数组的含义，表示以i为起始，j为结束的字符串s的最长回文子序列长度为dp[i][j]

2. 确定递推公式，首先是s[i] == s[j]的情况，dp[i][j] = dp[i + 1][j - 1] + 2，然后是二者不等的情况，就是dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])，这里就是要看看哪一个单独加入可以组成最长回文子序列

[i...i+1........j-1...j]

3. 初始化dp数组，这个比较特殊，不是像之前所有做过的动归一样是根据遍历顺序进行初始化的，而是在i和j相等的时候进行初始化，其余地方都初始化为0。这里还可以想，就是如果根据遍历顺序进行初始化，那么最下一行和最左一列的dp值根据定义没有办法得到，而唯一能得到的就是当i == j时dp[i][j] = 1

4. 确定遍历顺序，从下往上，从左往右。这里注意，就是在遍历j的时候，从i + 1开始，因为已经在初始化的时候对dp[i][i]进行了赋值，所以j的初始位置也要发生变化

5. 打印dp数组

LeetCode测试

注意这里最后return的时候，需要返回的是dp[0][s.size() - 1]表示以0开始和以s.size() - 1结束的整个s字串的最长回文子序列的长度

打印出来dp看一下，主对角线上方才有值

---

1 2 3 3 4 
0 1 2 2 3 
0 0 1 1 3 
0 0 0 1 1 
0 0 0 0 1 

点击查看代码

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
        for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i + 1; j < s.size(); j++) {
                if (s[i] == s[j]) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][s.size() - 1];
    }
};