Manacher算法(一个字符串中找到最长回文子串)

零、预备知识

　　Manacher用于在一个字符串中找到最长的回文子串。

　　回文串:正着念和反着念一样，例如aabbaa,anna等。

　　注意子串与子序列的区别：

　　　　子串必须是在原字符中可以找到的。比如 " I am a student"。am是子串（当然也是子序列），但是aa就不是子串了（是子序列）。

一、算法原理

　　Manacher算法通常人称马拉车算法，用于在一个字符串中找到最长的回文子串。

　　1.首先因为奇偶个数的不同，所以判断回文的方式不一样，因此manacher算法通过在字符串两边和每个字符之间插入一个相同的字符来字符串转换为奇数个的字符串。插入的字符可以是任意字符，但是必须保证插入的字符都相同，一般常用‘#’作为插入字符。例如，原始字符串aaabbbaaa,插入后的字符串则为#a#a#a#b#b#b#a#a#a#。

　　2.manacher算法使用了一个辅助数组pArr[](回文数组)来存储以每个位置i为中心的最长回文串的最右边界到位置i的距离。假设以i为中心的最长回文串左右边界分别为L,R，那么pArr[i]=R-i+1;

　　3.接下来就是计算字符串的回文数组pArr[]，计算时分两大情况:

　　　　3.1当前位置i不在回文右边界中，则向右边暴力扩张。

　　　　3.2当前位置i在回文右边界内(又分为三种情况):

　　　　　　3.2.1：i的回文半径彻底在R(以C（回文中心）为中心所能到达的最右边界)内，则R不用扩

　　　　　　例如:

　　　　　　3.2.2：i ’  的回文半径在L外面，每包住，此时i的回文半径为i到R。

　　　　　　例如: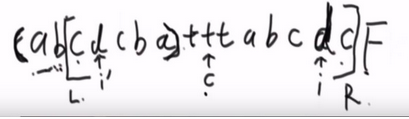

　　　　　　3.2.3：i'的回文半径压线，i与R之间的半径不用计算，但是不确定是否再向右扩

二、算法实现

public class Manacher {
    public static char[] manacherString(String str){  
        char[] charArr = str.toCharArray();
        char[] res = new char[str.length()*2+1];
        int index = 0;
        for(int i=0;i<res.length;i++){//01 10&01 100&001
            res[i] = (i&1)==0?'#':charArr[index++];
        }
        return res;
    }
    
    public static int maxLcpsLength(String str){
        if(str==null||str.length()==0){
            return 0;
        }
        char[] charArr = manacherString(str);//扩充后的字符串
        int[] pArr = new  int[charArr.length];//存储每个位置的最大回文长度
        int index = -1;//回文右边界中心  2*index-i是i位置关于index的对称点
        int pR = -1;//目前所能到达的最右边界
        int max = Integer.MIN_VALUE;
        for(int i=0;i!=charArr.length;i++){//对每个位置
            pArr[i] = pR>i?Math.min(pArr[2*index-i], pR-i):1;//起码回文的距离,看不用扩的区域是多少，是与之对称的点的回文半径限制了它还是它距离最右边界的距离限制了它
            while(i+pArr[i]<charArr.length&&i-pArr[i]>-1){//如果在范围内则往外扩
                if(charArr[i+pArr[i]]==charArr[i-pArr[i]]){
                    pArr[i]++;
                }else{
                    break;
                }
            }
            if(i+pArr[i]>pR){
                pR = i+pArr[i];
                index = i;
            }
            max = Math.max(max, pArr[i]);
        }
        return max-1;
    }
    
    public static void main(String[] args) {
        //String str = "abc1234321ab";
        String str = "1213121";
        System.out.println(maxLcpsLength(str));
    }
}