【软件工程】个人项目作业

教学班级：005，项目GitHub地址：https://github.com/CapFreddy/SoftwareEngineering_HW1

项目	内容
课程	2020春季计算机学院软件工程(罗杰 任建)
作业要求	个人项目作业要求
我的课程目标	章握软件开发的方法论和诸多技术，与同学合作开发出好的软件
本次作业的作用	实战体验个人开发过程；掌握C++基本数据结构

解题思路描述

  拿到题目后，第一反应是最简单的两两求交点：对于给定的\(n\)个几何对象，两两求交点后将交点放入集合中，最后输出集合的大小，时间复杂度为\(O(n^2)\)。随即发现，性能测试中几何体最多可以达到\(500000\)个，而最多却只有\(5000000\)个交点——即便在全部为直线的情况下，\(500000\)条直线最多产生\(124,750,000,000\)个交点——这说明存在大量的平行/多线交于一点。而在多线共点广泛存在的情况下，两两求交点浪费了许多计算量。

  建立这样一个认识后，开始寻找优化的算法，并在Stack Overflow找到Calculate the number of intersections of the given lines的问题。虽然问题下没有给出解决的算法，却有人提到了”\(n\)条线段求交点“的Bentley-Ottmann算法。该算法在\(n\)条线段形成\(k\)个交点时时间复杂度为\(O((n+k)\log{n})\)，这意味着在\(k=o(\frac{n^2}{\log{n}})\)的情况下优于穷举法。算法通过维护一个结点队列及扫描线链表，以交点的产生推进，从而避免了重合结点的重复计算。”求N条线段的所有交点——Bentley-Ottmann算法“提供了一个比较简明的算法描述。

  当几何体为直线时，将初始扫描线定至\(x\)轴，算法推进过程仍然适用。由于直线的无限性，除与\(x\)轴平行的（这些直线可以通过穷举法解决）之外的所有直线在任何情况下都与扫描线相交，因此算法的过程实际上简单了一些。然而实现过程中，在解决了诸多数据结构的问题后卡在了对象经过容器传递后指针丢失的问题上，考虑到附加题的扩展性便回归了原始做法。

PSP表

PSP2.1	Stages	Estimation Time Cost(minute)	Time Consumed(minute)
Planning	计划
· Estimate	估算任务总时长	30	30
Development	开发
· Analysis	需求分析/学习新技术	150	180
· Design Spec	制作设计文档	30	30
· Design Review	设计复审	0	0
· Coding Standard	代码规范	15	15
· Design	具体设计	60	80
· Coding	具体编码	240	300
· Code Review	代码复审	30	30
· Test	测试	60	60
Reporting	报告
· Test Report	测试报告	60	1
· Size Measurement	计算工作量	20	20
· Postmortem & Process Improvement Plan	总结	30	30
	合计	725	855

设计实现过程

  类设置采用每种几何对象单成一类的方式，设置了直线、圆和结点类。在几何对象类内设有如下方法：

• 几何对象的构造方法（由输入的字符串构造）。
• 判断与其它几何对象位置关系（如是否有交点）的方法。
• 求解与其它几何体交点的方法（特别地，直线和圆的相交由直线类处理）。

此外设置一个几何对象的容器类，除用于装载外还负责遍历计算交点。

  对于计算出的交点使用unordered_set进行无重复存储，其原理即为一个哈希表。对于插入的元素首先计算其哈希值，而后将其放入对应的地址中。若存在冲突则判断是否与冲突元素相等，若不等才将其插入。因此对于自己构造的节点类，需要提供自定义的hash函数以及比较函数以确定其哈希计算方法及发生冲突时的比较方法（相关代码见性能改进部分）。

单元测试

  单元测试根据几何对象之间可能的相对位置设计测试样例。由于主程序依赖于命令行输入，需要在主类中另设测试接口，并添加输出几何对象相关信息的接口以协助锁定bug。

  在单元测试中为仅含直线、仅含圆以及含有直线和圆的情况各设计了5个测试样例。5个样例呈递进关系，为：仅有一个几何对象->多个几何对象相离->多个几何对象两两相切->多个几何对象两两相交->复杂的相交情况。涵盖了几何对象间相离、相切、相交以及多个几何对象交于一点的情况，的确帮助找到了一些bug。主要是在计算中未强制转换变量类型造成的问题。另外值得说明的是一个精度引起的bug：测试左图样例时发现输出比预期多了2，查看其交点坐标如右图：

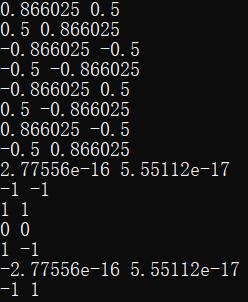
可以看到，在第9行和第14行，由于计算精度问题本应是\((0,0)\)的点被算成了一个非常接近原点的点。这可能是由于计算过程中产生的无限小数造成的精度损失（如\(4 / 3.0 * 3 - 4 * 3 / 3.0\ne0\)）。虽然其能被自定义的相等函数判别为与原点相等，但其因哈希值与\((0,0)\)不同而被分配至不同的bucket，因此无法筛重。

  对此的解决方法是修改节点类哈希值计算方法：若以\(EPS\)的进度判断相等，则将结点类的哈希值计算方式改为：

hash<double>{}(round((node->m_x + node->m_y) * 1.0 / EPS))

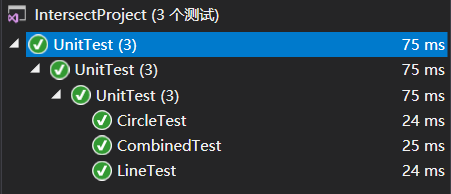
修改之后通过了所有测试：

效能分析和性能改进

  对程序运行时间提升最大的改进一是引入unordered_set来存储交点，重载元素的哈希值计算方法及比较方法（如下图）；二是容器中只存指针，避免了存对象时的复制操作。这两项改进明显降低了程序运行时间。

struct NodePointerHasher
{
	size_t operator()(const Node* node) const noexcept
	{
		return hash<double>{}(node->m_x + node->m_y);
	}
};

struct NodePointerComparator
{
	bool operator()(const Node* node1, const Node* node2) const noexcept
	{
		return fabs(node1->m_x - node2->m_x) <= EPS && fabs(node1->m_y - node2->m_y) <= EPS;
	}
};

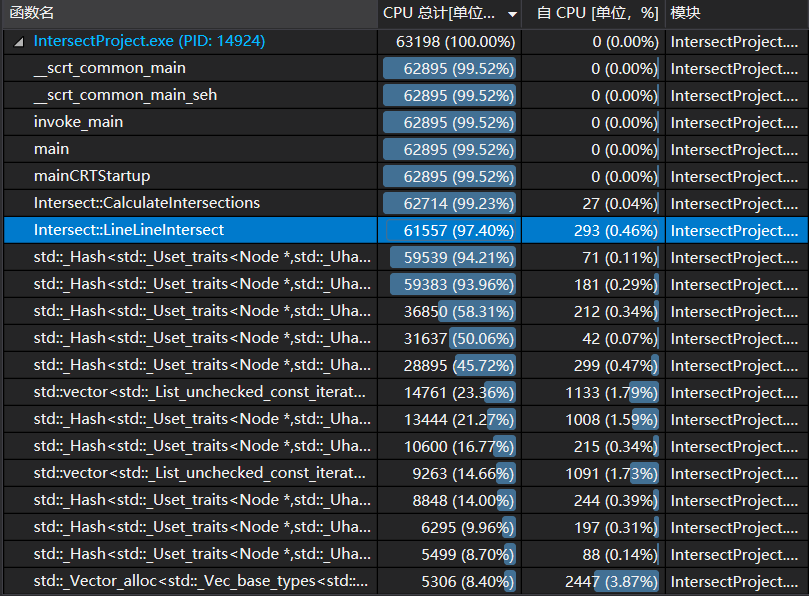
  调整数据结构后，算法在随机生成的10000条数据中的表现如下。可以看到，直线之间求交点是占用CPU时间最长的子函数。对此的一个优化方法是在读入数据时将未来要使用的量（行列式、斜率等）提前算好，避免重复计算。

代码说明

  项目的核心部分是几何对象交点的计算，相关代码如下：

· 直线与直线的交点通过联立二元一次方程组求解。

vector<Node> IntersectLine(Line line)
{
    double x, y;
    vector<Node> intersections;

    if (!parallels(line))
    {
        if (this->m_vertical)
        {
            x = m_x1;
            y = line.m_k * ((double)m_x1 - line.m_x1) + line.m_y1;
        }
        else if (line.m_vertical)
        {
            x = line.m_x1;
            y = m_k * ((double)line.m_x1 - m_x1) + m_y1;
        }
        else
        {
            x = (double)(m_k * m_x1 - line.m_k * line.m_x1 + line.m_y1 - m_y1) / (m_k - line.m_k);
            y = (double)m_k * (line.m_k * ((double)m_x1 - line.m_x1) + (double)line.m_y1 - m_y1) / (m_k - line.m_k) + m_y1;
        }
        intersections.push_back(Node(x, y));
    }
    return intersections;

· 直线与圆、圆与圆皆依赖圆方程建立二次方程求解。

vector<Node> IntersectCircle(Circle circle)
{
    vector<Node> intersections;
    int baX = m_x2 - m_x1;
    int baY = m_y2 - m_y1;
    int caX = circle.getX() - m_x1;
    int caY = circle.getY() - m_y1;

    int a = baX * baX + baY * baY;
    int bBy2 = baX * caX + baY * caY;
    int c = caX * caX + caY * caY - circle.getR() * circle.getR();

    double pBy2 = (double)bBy2 / a;
    double q = (double)c / a;

    double disc = pBy2 * pBy2 - q;
    if (disc >= 0)
    {
        double tmpSqrt = sqrt(disc);
        double abScalingFactor1 = -pBy2 + tmpSqrt;
        double abScalingFactor2 = -pBy2 - tmpSqrt;

        intersections.push_back(Node(m_x1 - baX * abScalingFactor1, m_y1 - baY * abScalingFactor1));
        if (disc != 0)
        {
            intersections.push_back(Node(m_x1 - baX * abScalingFactor2, m_y1 - baY * abScalingFactor2));
        }
    }
    return intersections;
}

vector<Node> Intersect(Circle circle)
{
    double d, a, h, x2, y2, x3, y3, x4, y4;
    vector<Node> intersections;

    d = sqrt((circle.m_x - m_x) * (circle.m_x - m_x) + (circle.m_y - m_y) * (circle.m_y - m_y));
    if (intersects(circle, d))
    {
        a = ((double)m_r * m_r - (double)circle.m_r * circle.m_r + d * d) / (2 * d);
        h = sqrt((double)m_r * m_r - a * a);
        x2 = m_x + a * ((double)circle.m_x - m_x) / d;
        y2 = m_y + a * ((double)circle.m_y - m_y) / d;
        
        if (d < 1e-6)
        {
            Node intersection(x2, y2);
            intersections.push_back(intersection);
        }
        else 
        {
            x3 = x2 + h * ((double)circle.m_y - m_y) / d;
            y3 = y2 - h * ((double)circle.m_x - m_x) / d;
            x4 = x2 - h * ((double)circle.m_y - m_y) / d;
            y4 = y2 + h * ((double)circle.m_x - m_x) / d;
            Node intersection1(x3, y3);
            Node intersection2(x4, y4);
            intersections.push_back(intersection1);
            intersections.push_back(intersection2);
        }
    }
    return intersections;
}

收获/后继目标

  本次作业中对算法的尝试卡在了容器传值时指针发生的变化，后续计划更加详尽地了解C++运行时内存分配以更自如地运用指针。同时多积累数据结构使用技巧，提高编码效率。在设计方面，可以设置一个几何对象基类，具体的几何对象继承自基类，这样比较方便管理。