OO第一单元总结
前言·文前约定
第一单元的三次作业递进关系明显,然而在经历了两次彻底的重构后,对面向对象中继承、多态的特性和代码复用的思想有了一定认识。
为行文方便,约定表达式(Poly)中由加号相连接的单元称为项(Term),项内由乘号相连接的单元称为因子(Factor)。
第一次作业
第一次作业中项的形式很简单:项内仅有一个单项式因子。这也就意味着一个项可由其中x的系数和指数完全刻画出来。因此我将表达式视为系数和指数构成的两个下标一一对应的数组。
(1) 基于度量分析程序结构
类属性与关系:
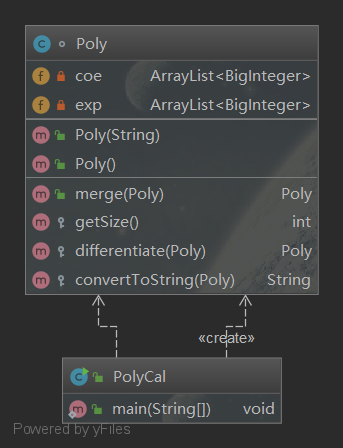
这种实现方式虽然能很直观地完成这次作业的任务,对表达式的化简也相对容易。但多项式类完全没有灵活性。一旦项的形式改变,整个类内的方法都要推翻重写。
方法:

可以看到,Poly类传入String的构造方法的圈复杂度很高,这是因为这一构造方法承担了合法性检查,按符号分割项,提取项的系数和指数这三个相对独立的工作。这些工作的整合使得调试变得很困难。
(2)Bug分析
第一次作业出现的bug是由于在正则表达式中使用\s匹配空白字符所致。对文档中空白字符的范围的理解有误。
(3)互测策略
在阅读一份互测代码发现有负系数处理不当的问题后针对系数、指数的四种符号组合构建了一些测试用例。测试时又发现了一些化简时产生的问题,如化简系数为1的项时输出了乘号。
第二次作业
第二次作业中项的形式有所变化:项可以由因子相乘构成,因子中也加入了简单三角函数。虽然如此,每一项仍然可以由系数,x的指数,sin(x)的指数以及cos(x)的指数四个参数完全表征。因此我将表达式视为项的集合,将项视为四个参数的集合。类之间的层级结构开始显现。
(1) 基于度量分析程序结构
类属性与关系:

在Poly类中将判断输入合法性与按符号分割项作为两个由构造函数调用的方法,疏解了构造函数的功能。在构造时直接求导虽然省去了存储输入表达式的工作,但降低了代码的复用性。
方法(节选高复杂度):
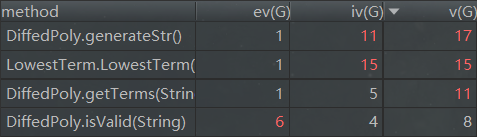
圈复杂度较高的几个方法涉及输出时的化简,项参数的提取等。由于可能的情况较多,其圈复杂度必然较高,但合理的判断顺序能有效降低圈复杂度。
(2)互测策略
首先使用上次互测时构建的数据做简单的符号检查,然后针对项内不同因子的组合情况构建了一些测试样例。发现了一些三角函数因子求导的问题。
(3)重构思路
由于本次作业中项变得复杂,再统一到Poly类中会导致Poly类过于臃肿。故创建Term类进行管理。其可由从Poly类中分割出的字符串形式的项构造。
第三次作业
本次作业中由于嵌套因子的存在无法将项归结为有限个参数的集合。但化归的思想可以通过继承的方式实现:创建一个因子抽象类,因子的所有具体形式都继承这个抽象类(包括表达式和嵌套型因子)。表达式仍然视为项的集合。而项视为因子的集合。
(1)基于度量分析程序结构
类属性与关系:
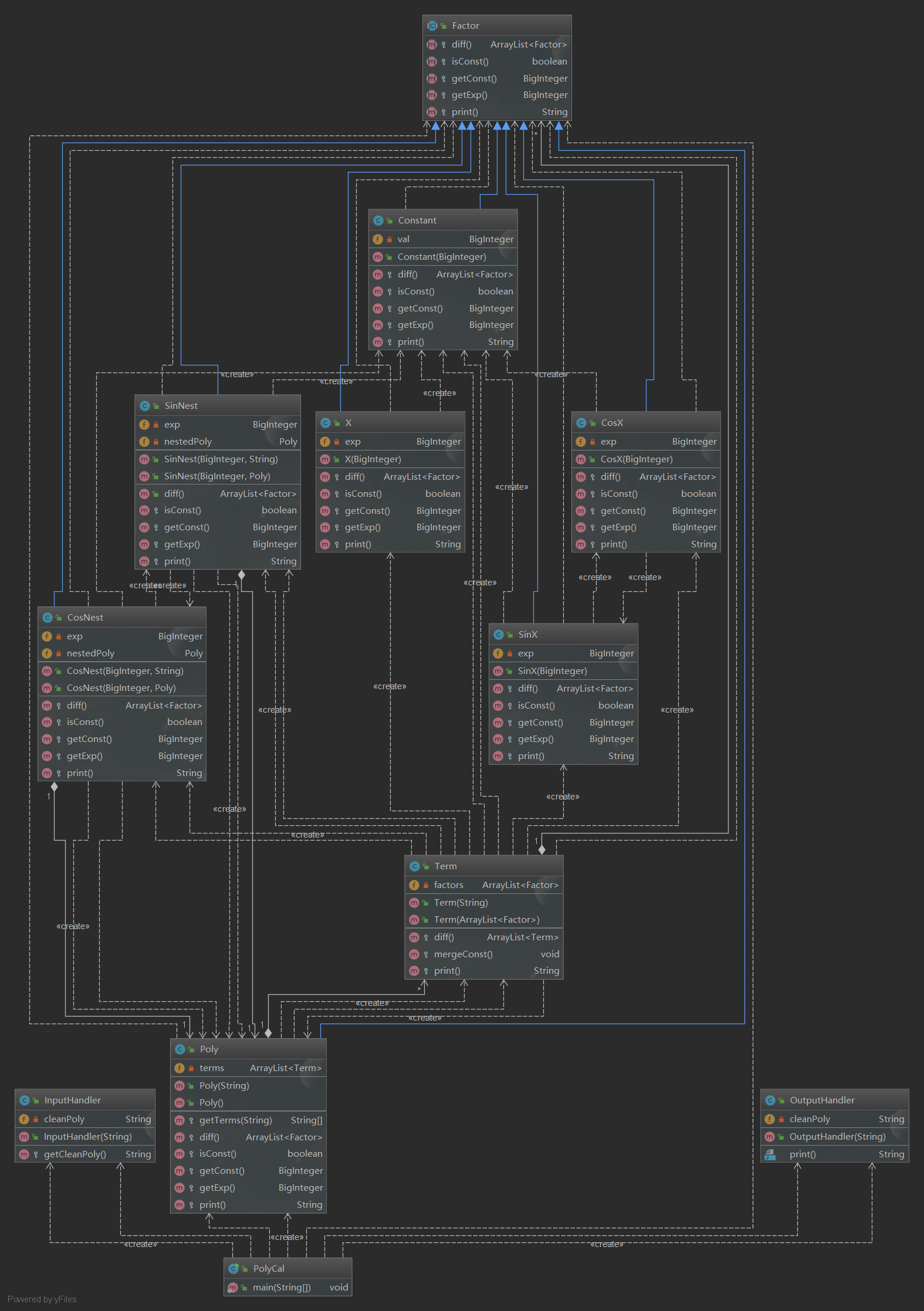
继承的使用让求导和输出变得简单,各层级的求导只需要考虑当前层次的求导规则:多项式是项的相加,因此求导为各项求导之和;项是因子的相乘,因此求导按照链式法则处理;嵌套因子则按照复合函数求导法则求导;普通因子即按照相应求导规则求导。创建输入处理类首先判断输入合法性的目的是让在递归中“流通“的字符串皆为合法的,避免在嵌套复杂时由括号导致的判断错误。
方法:

由于因子的可能形式众多,拆分过程比较复杂。
(2)Bug分析
互测中被发现的bug是由于在一个双层循环中本该用内层循环变量索引时使用了外层循环变量。此问题是在编写过程中使用复制粘贴批量生产的,提交之前发现了问题但并未改正完全。
(3)互测策略
本次互测使用对拍器找出了一些bug。阅读了同学写的对拍器后对其原理有了一定认识。
(4)重构思路
由于绝对无法用有限个简单参数表示项,开始构建抽象化的表达式结构,即表达式-项-因子。
Applying Creational Pattern
对代码结构的进一步优化可以通过合并一些重复代码实现,如创建括号处理类解决外层括号中内容替换。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号