Chapter3_Linear Models for Regression(讨论课)

讨论课提纲：

• 自我介绍
• 简单说一下回归的主要问题，给定数据集，找出输入和输出之间的关系，对于一个新的输入可以预测其输出

•  我们将从两个角度来讨论这个问题，一个是传统的频率学派，利用极大似然估计进行分析，首先利用极大似然估计估计参数，并找出其与最小二乘法之间的联系，然后从几何角度理解最小二乘法。因为样本数量可能会很大，所以我们将采用在线学习的方式就行。同时因为极大似然估计是有偏估计，其估计结果也与样本有较大联系，所以加入正则项并通过偏差-方差对误差结果进行分解。
• 另一个是贝叶斯学派，认为目标值满足一定的概率分布，从而估计目标值的后验分布。这里分为两个步骤，第一个步骤是估计参数的后验分布，利用假设的参数的先验分布，和独立采样得到的似然函数得到参数的后验分布。再利用参数的后验分布结合似然函数，关于参数积分，即得到了预测分布，知道了预测分布以后，我们就可以利用期望作为对目标值的估计。得到了期望值以后，我们会发现，贝叶斯线性回归方法还有另一种形式，即利用等价核进行估计。

 

• 首先介绍一下广义线性函数，之所以称为广义线性函数，是因为它关于系数是满足线性关系的，但是基函数的选择却可以是非线性函数。

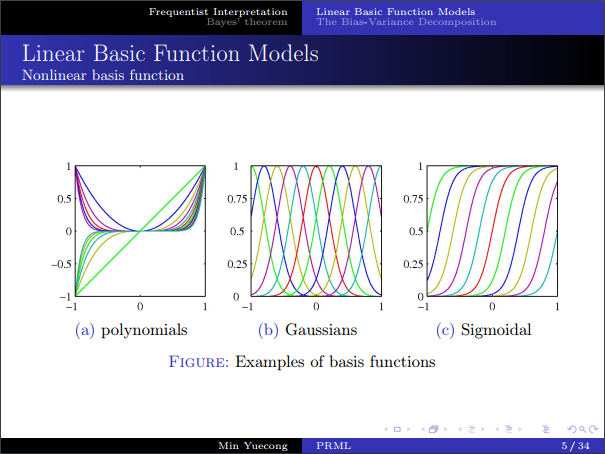
• 常用的几种基函数，其实Taylor级数和傅里叶级数也可以看做一种广义线性回归。（书上公式推导有误，sigmoid 和 tanh 的关系）

• 回顾一下1.5节的内容，我们采用平方loss函数得到的期望损失函数，用来衡量y(x)和t之间的差距。

 

• 利用变分法我们可以得到损失函数的期望关于y(x)求偏导为0时对应的y(x)即是t在x的条件期望，即在y(x)=E[t|x]时，损失最小。

• 同时我们可以发现期望损失函数可以进行分解（板书推导，书上公式有误），得到两项，一项是噪声而另一项则是说明在平方损失函数的条件下，最优的近似即是条件期望。
• 同时可以从平方损失函数推广到更一般的情况。

 

• 现在我们开始考虑极大似然和最小二乘法之间的关系，这里我们采用平方误差函数。假设数据有高斯噪声，数据是独立采样，从而推导出对数似然函数。

• 最大化对数似然函数实质上就是最小化平方误差函数，求偏导得到的w的表达式，我们这是会发现，和最小二乘法的正规方程组具有相同的形式。
• 注意一下设计矩阵，每一行是一个数据，每一列是一个基函数在每个数据点上的值。
• 广义逆矩阵（板书）

• 关于w_0和xb求偏导，得到解释：w_0是目标均值和估计均值之间的偏差，而xb则是和目标值的残差方差相关。

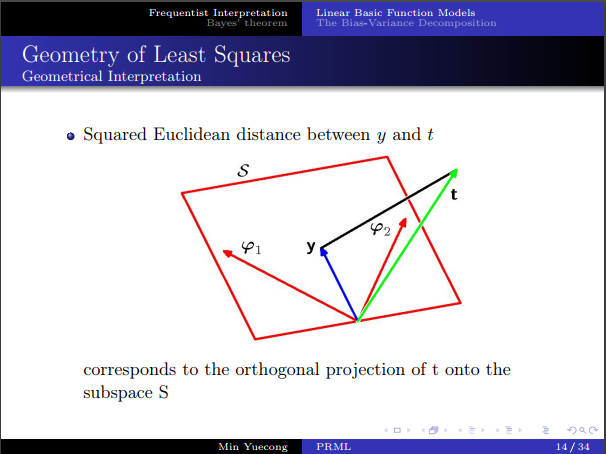
• 最小二乘的几何解释：子空间上的正交投影

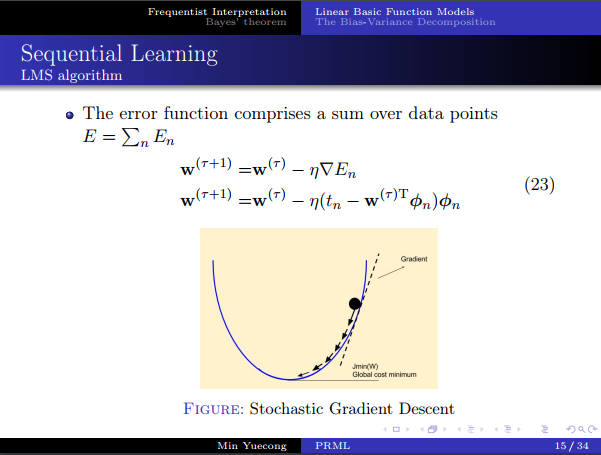
• 会注意到求逆矩阵的时候和特征维数有关，而且随着样本数量的增加，计算复杂性也随之增加，所以考虑在线学习的方法。

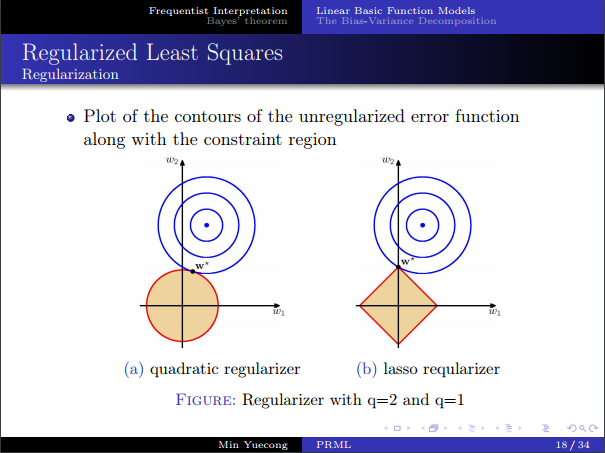
• 考虑一下正则项，可以看作一个约束问题，从几何上看，L1正则是稀疏的，而L2正则代数性质会更好一些，之后会从贝叶斯角度对正则项再进行解释。

 

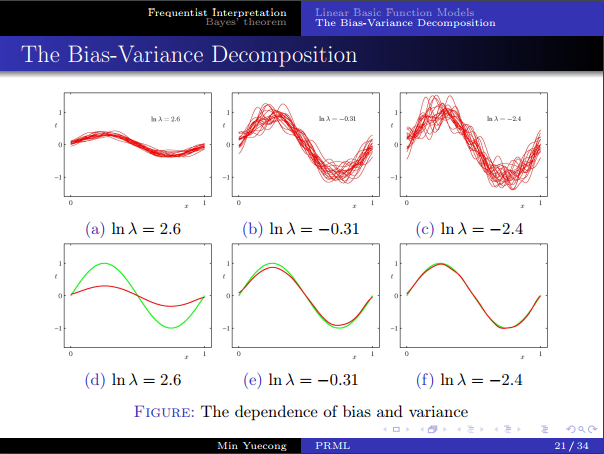
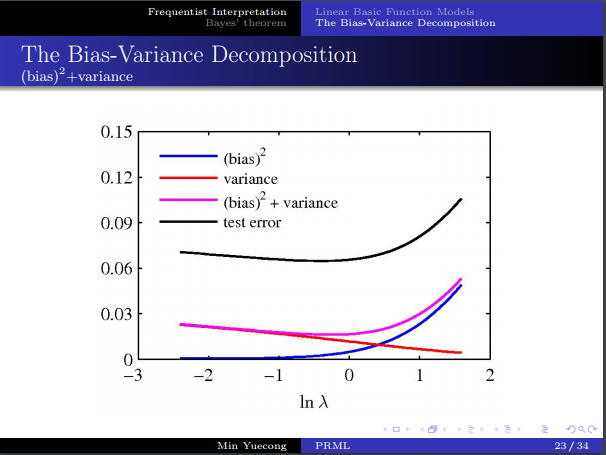
• 偏差方差分解，如果说数据无限大，则可以无限近似目标函数，但现实做不到，所以我们估计的误差会与数据集的选取相关。
• 考虑对误差进行分解，得到了bias和variance。
• 需要在二者之间进行权衡。

 

• 贝叶斯线性回归

• 回顾一下贝叶斯公式

• 参数的后验概率的计算

• 与带有二次正则项的极大似然具有相同的形式。
• Laplace分布-L1正则，Gaussian分布-L2正则。

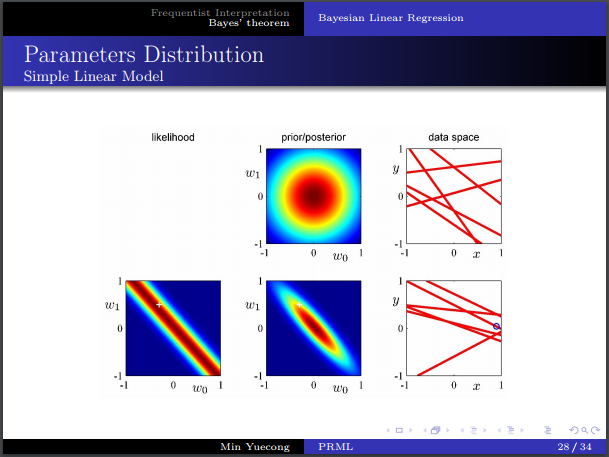
• 从图像上理解先验，似然和后验，样本对于概率分布的影响。

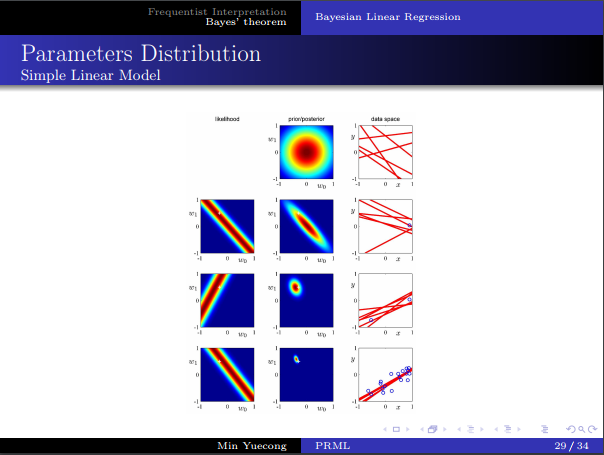
• 先验、后验概率的转换，迭代的使用。

• 预测分布的推导。

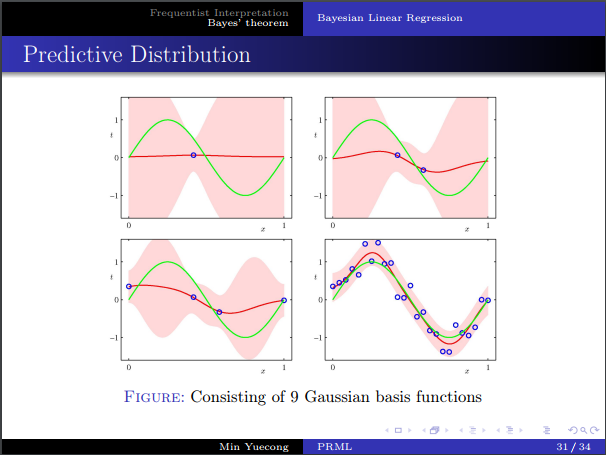
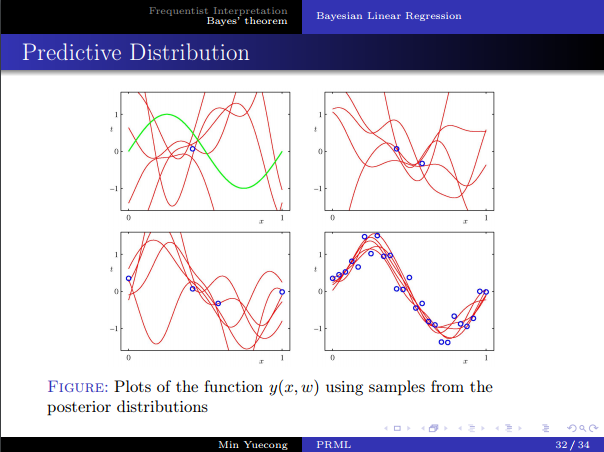
• 直观几何解释。

• 等价核的定义。

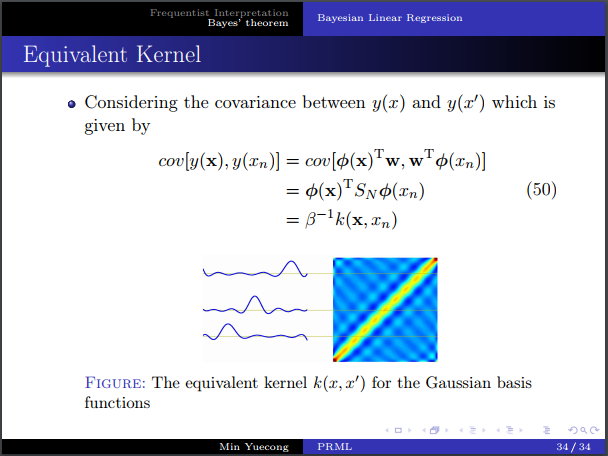
• 等价核和相关系数之间的关系。等价核和为1的推导，直观理解，矩阵乘法。

 

 

大致整理了一下思路，希望明天晚上讲的时候语速慢一点，条例清晰一点，之后再更。