笔记——树状数组
蓝月の笔记——树状数组篇
在可恶的OI里，我们尝尝会遇到一些区间问题，例如区间修改单点查询，单点修改区间查询，区间修改单点查询，单点修改单点查询。
其中，单点修改区间查询，就是树状数组最经典的用法啦！
给定一个长度为 \(n\) 的序列 \(a_1,a_2,\cdots,a_n\) 和两种操作：
- 输入
1 x k将 \(a_k\) 加上 \(x\)； - 输入
2 l r，求 \(\sum_{i=l}^r a_i\) 。
这就是我们说的单点修改区间查询。
根据前缀和的思想，我们可以用一些手法求出每一个 \([1,x]\) 的和。查询时直接输出 \(Q(r) - Q(l)\) 即可。（\(Q(x)\) 为查询 \(\sum_{i=1}^x a_i\) 的函数）
首先我们设树状数组的数组（？）为数组 \(c\)。
定义 \(c_x\) 表示树状数组这棵树中 \(x\) 的所有子节点的 \(c_i\) 总和，即 \(c_x = \sum_{i}^{i \in \text{son of x}} c_i\)
\(\operatorname{lowbit}\)
我们引入一个函数，叫 \(\text{lowbit}\)，从避免可知，\(\operatorname{lowbit}\) 就是最 \(\operatorname{low}(\texttt{低})\) 的 \(\operatorname{bit}(\texttt{二进制位})\)，即二进制中最低位的 \(1\)。
举个例子：
\(\qquad\qquad\qquad\quad\downarrow\)
\(\qquad\qquad\qquad\quad\,\vdots\)
\(\because x = 18 = (10010)_2\)
\(\qquad\qquad\qquad\quad\,\vdots\)
\(\qquad\qquad\qquad\quad\uparrow\)
\(\therefore \text{lowbit}(x) = 2 = (10)_2\)
\(\operatorname{lowbit}\) 怎么求呢，这时候就要用到补码的特性了。
我们注意到 \(x\) 和 \((\sim{x}) + 1\) 的二进制，我们求的最低位的 \(1\) 一直到最后一位都没有变化，这一段是 \((100\cdots0)_2\)，而前面的部分全部取反。
我们充分发扬人类智慧，将 \(x\) 与 \((\sim{x}) + 1\) 按位与，就可以把前面的全部消掉，而留下 \((100\cdots0)_2\) 这一部分，而这，就是我们要求的 \(\operatorname{lowbit}\)！
而根据补码的性质 \((\sim{x}) + 1 = (-x)\)，所以我们可以得到求 \(\operatorname{lowbit}\) 的代码：
int L(int x) {
return x & -x;
}
如果你喜欢写成宏定义的话：
#define L(x) ((x) & (-x))
还是已 \(x=18\) 为例：
我们前面手算的也是 \(2\)，这就证明了 \(\text{lowbit} = x \& -x\)
\(\operatorname{update}\)
先放图。
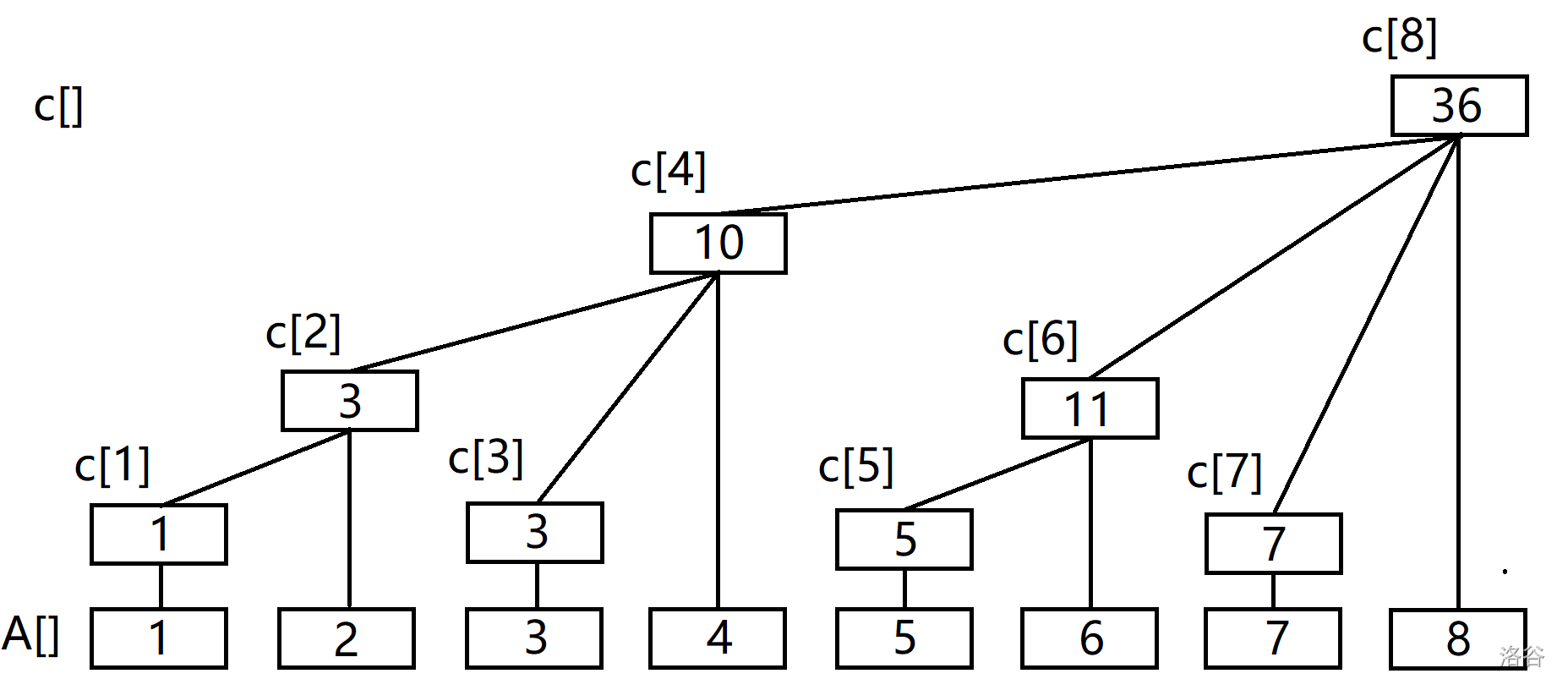
【图片转载自liruixiong0101的blog】
观察这棵树，可以发现 \(c_i\) 的父亲为 \(c_{i + \text{lowbit}(i)}\)，而根据 \(c\) 的定义 \(c_x\) 一定在 \(c_{i + \text{lowbit}(i)}\) 里面，然后我们循环迭代递推，所以我们可以得到 \(\text{update}\) 的代码：
void U(int x, int y) {
for (int i = x; i <= n; i += L(i)) {
c[i] += y;
}
}
\(\text{query}\)
根据设计，\(\text{query}\) 求的是 \(\sum_{i=1}^{x}a_i\) 而不是 \(\sum_{i=l}^{r}a_i\)！！！
根据定义，\(c_x\) 代表 \(\sum_{i=x - \text{lowbit}(x) + 1}^{x}a_i\)，我们可以把 \(\text{query}\) 操作抽象成跳跃的过程。
我们现在 \(x\) 的位置，我们的目标是跳到 \(1\)，根据 \(c\) 的定义，我们先往前跳 \(\text{lowbit}(x)\) 格，也就是跳过 \(c_x\) 管辖的区间，这时 \(ans \gets c_x\)。
现在我们在 \(x-\text{lowbit}(i)\) 的位置，我们令 \(i \gets x-\text{lowbit}(i)\)，我们再往前跳 \(\text{lowbit}(i)\) 格，正好跳过 \(c_i\) 的管辖区间，这时 \(ans \gets c_x + c_i\)。
一直持续这个操作，直到 \(i \le 0\)，我们就得到了 \([1,x]\) 之间不重不漏的区间和了。
根据思路写出代码：
int Q(int x) {
int ans = 0;
for (int i = x; i; i -= L(i)) {
ans += c[i];
}
return ans;
}
然后求 \(\sum_{i=l}^{r}a_i\) 就可以很轻松了，即 Q(r) - Q(l - 1)。
\(\text{code}\)
然后我们就可以写完这道水黄力！（喜
已用结构体封装好的代码：
// P3374
#include<bits/stdc++.h>
using namespace std;
const int kMaxN = 5e5 + 5;
int L(int x) {
return x & -x;
}
struct BIT {
int n, a[kMaxN], c[kMaxN];
void U(int x, int y) {
for (int i = x; i <= n; i += L(i)) {
c[i] += y;
}
}
int Q(int x) {
int ans = 0;
for (int i = x; i; i -= L(i)) {
ans += c[i];
}
return ans;
}
};
int m, op, l, r;
BIT t;
int main()
{
cin >> t.n >> m;
for (int i = 1; i <= t.n; i++) {
cin >> t.a[i];
t.U(i, t.a[i]);
}
for (; m; m--) {
cin >> op >> l >> r;
if(op == 1) {
t.U(l, r);
} else {
cout << t.Q(r) - t.Q(l - 1) << '\n';
}
}
return 0;
}
友情给出树状数组结构体：（\(\text{lowbit}\) 要自己写）
struct BIT {
int n, a[kMaxN], c[kMaxN];
void U(int x, int y) {
for (int i = x; i <= n; i += L(i)) {
c[i] += y;
}
}
int Q(int x) {
int ans = 0;
for (int i = x; i; i -= L(i)) {
ans += c[i];
}
return ans;
}
};
