线性代数笔记01
蓝月の笔记——线性代数
引入一些数作为坐标是一种鲁莽的行为。
向量
我们先来了解线性代数的本质——向量
向量有三种表示方式
- 图像
- 符号
- 矩阵
在数学中,图像表示的向量,是一条平面直角坐标系上原点
下面给出一个向量的三种表示方式。
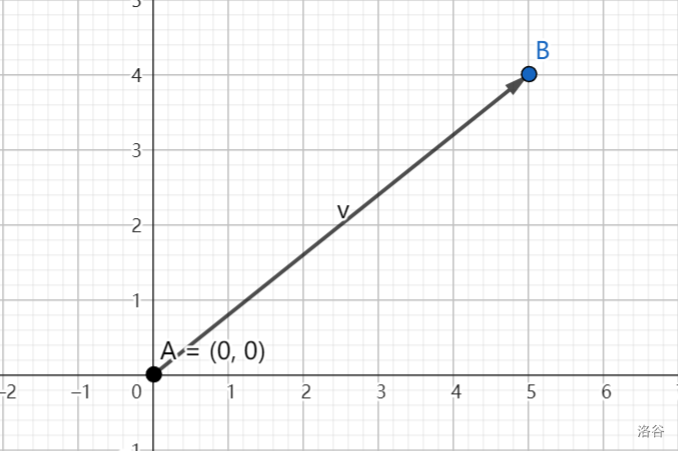
他们都表示一个从
另一种理解方式:
之后的学习中,我们会把这三种向量一起用,第一种用来画图表示,第二种用来书写,第三种用来计算。
向量的加法
接下来考虑向量的计算。(这一段配合视频中的动画更佳)
设向量
在图中表示为
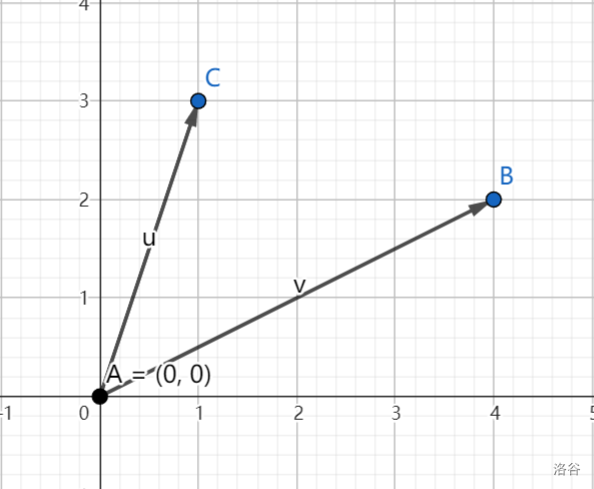
定义
在图中表示为
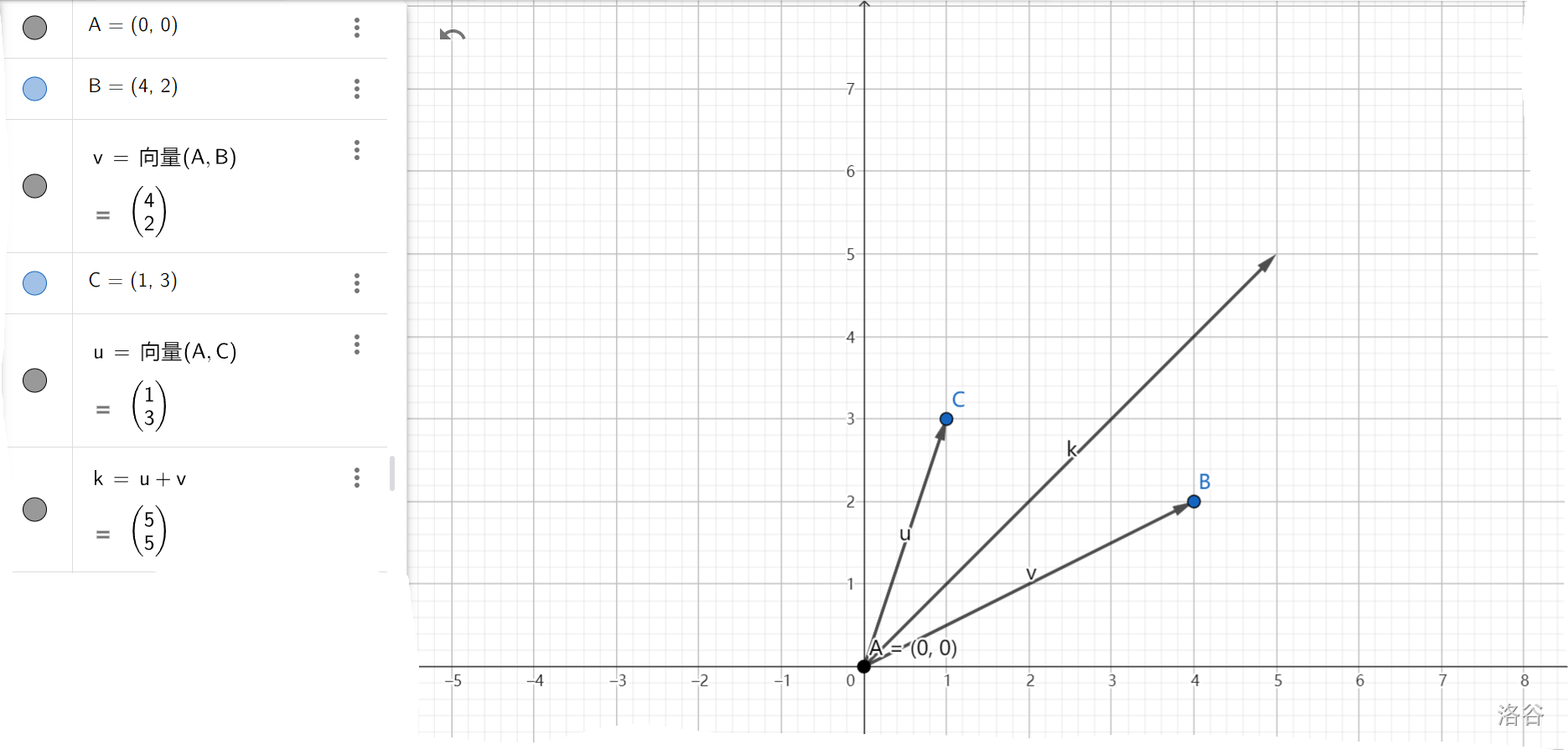
根据第二种向量的理解方式,
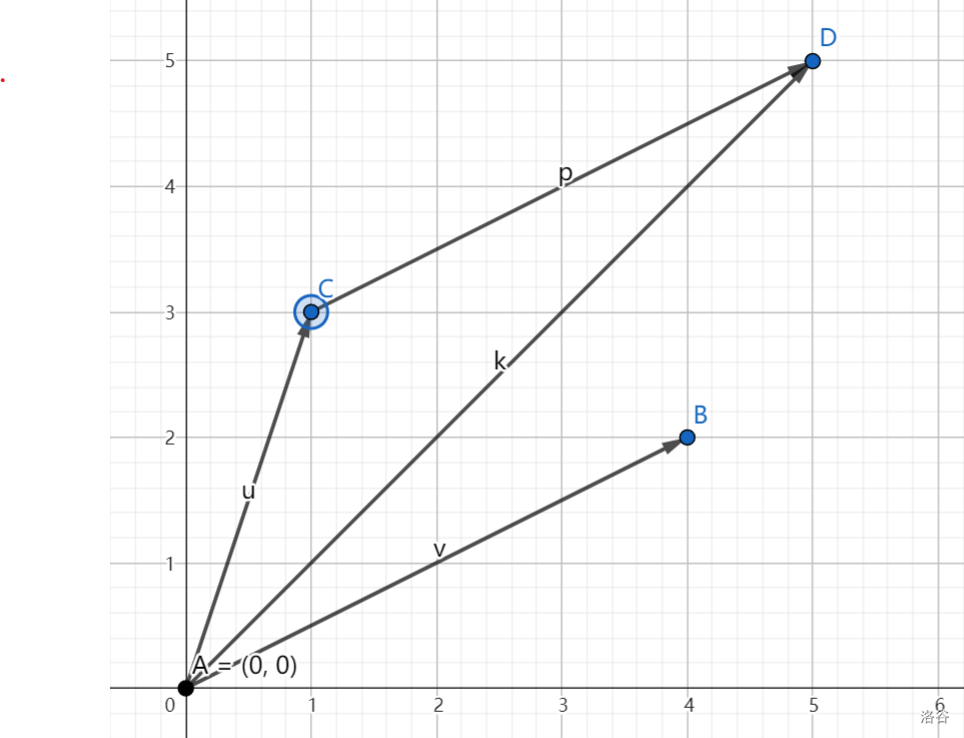
公式:
向量的数乘
顾名思义,向量的数乘就是一个向量乘上一个数
举个例子
那么可以得到
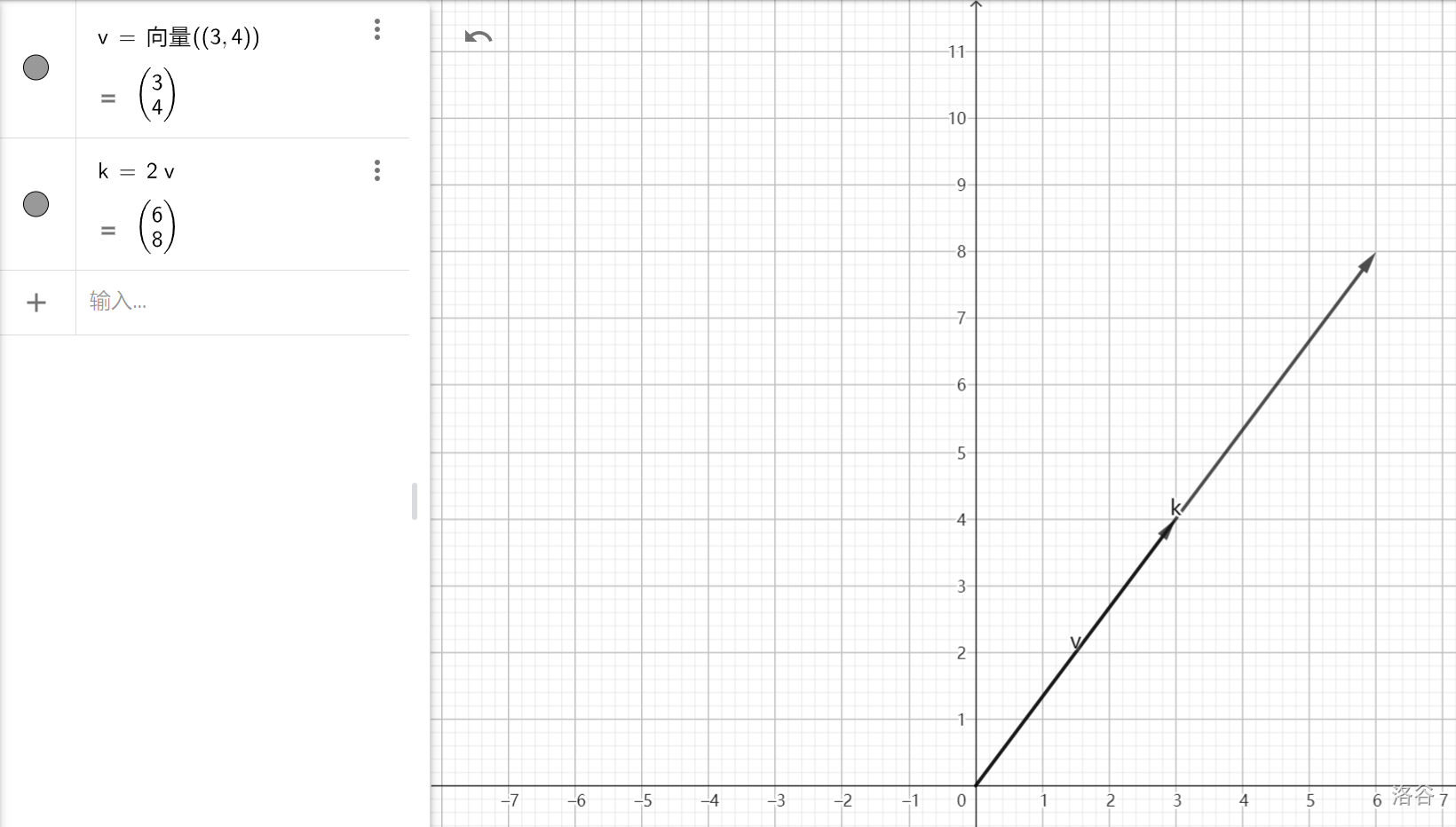
还是根据向量的第二种定义来理解
- 最开始在原点
- 执行以下操作
-
- 右移
- 右移
-
- 上移
- 上移
在上面的操作中,一共右移了
公式:
缩放
这不是一种运算。
易知,当
那么每一个
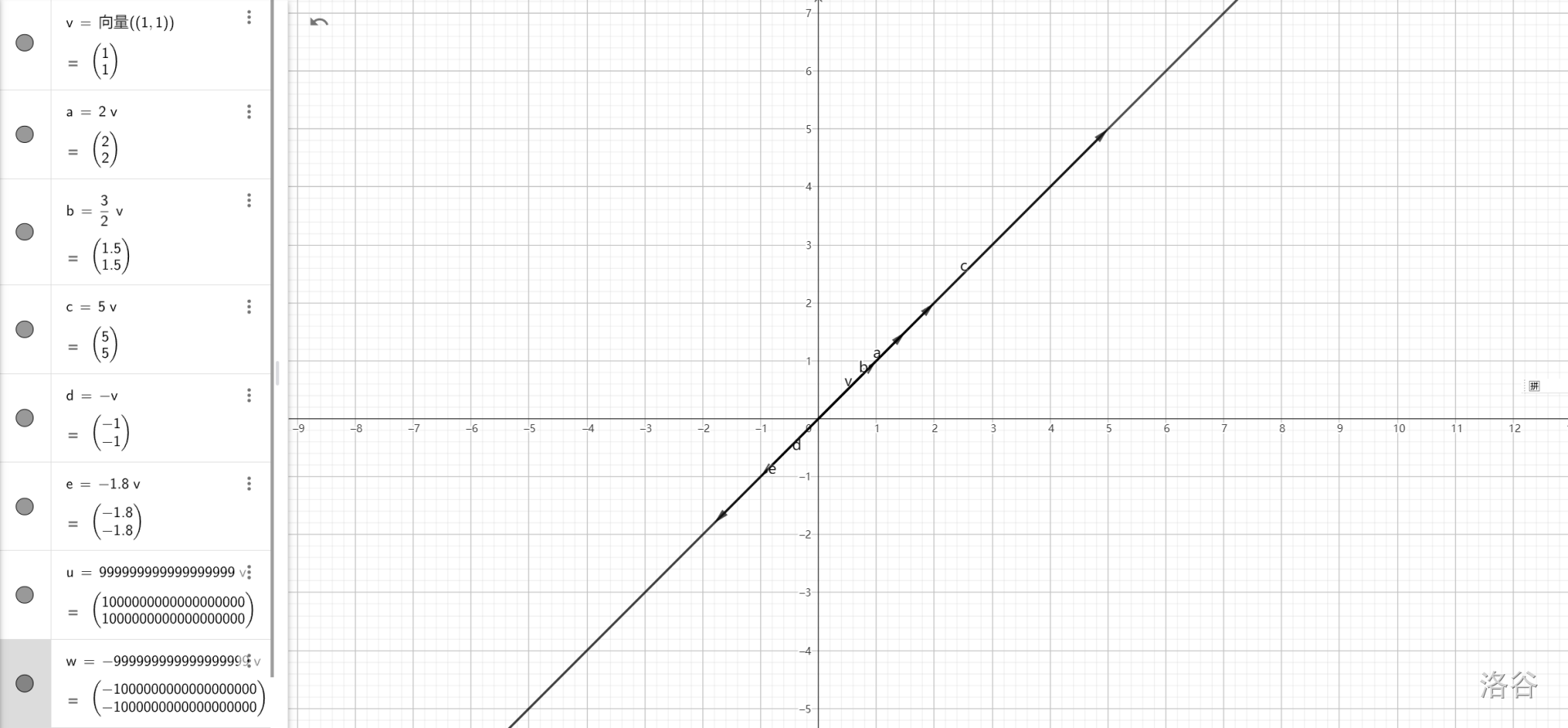
(打不出
特别地,当
那么我们定义一个之后会广泛应用的名词:标量。
标量
将向量
- 当
- 当
- 当
三维向量
定义几乎和二维向量没什么区别,运算和二维向量一模一样。
定义
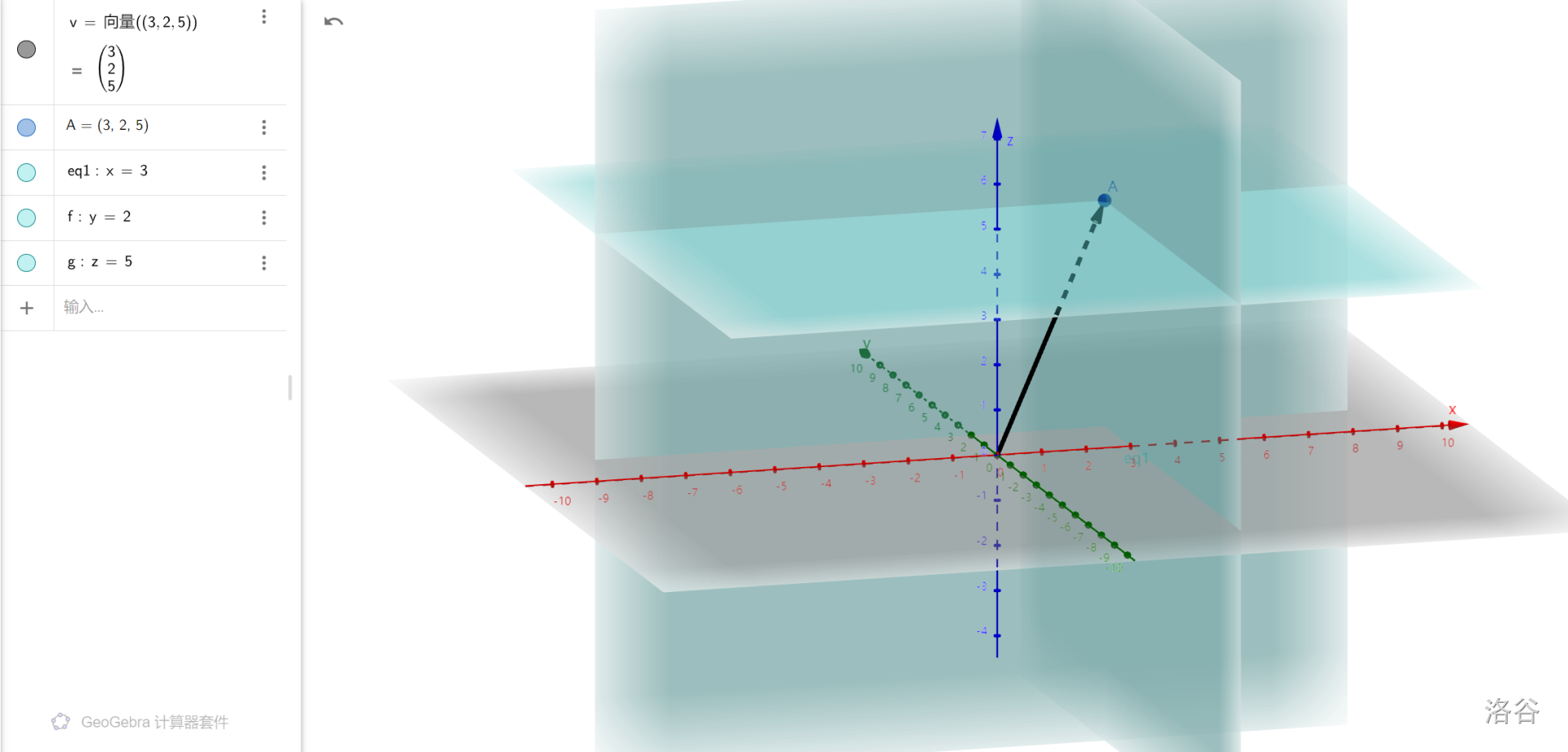
都是一条
计算:
加法:
数乘:
缩放同理。
本章总结
二、三维向量的定义、加法、数乘。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享4款.NET开源、免费、实用的商城系统
· 全程不用写代码,我用AI程序员写了一个飞机大战
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· 白话解读 Dapr 1.15:你的「微服务管家」又秀新绝活了
· 上周热点回顾(2.24-3.2)