支持向量机（Support Vector Machine）

本博客是针对Andrew NG在Coursera上发布的Machine Learning课程SVM部分的学习笔记。

目录

• 前言
• 最优化目标(Optimization Objective)
• 最大化边界的直觉（Large Margin Intuition）
• 最大化边界分类的数学原理(Mathematics Behind Large Margin Classification)
• 核（Kernel）
• 实际使用SVM的技巧

前言

相比logistic regression和neural network，SVM作为一种可以学习到复杂非线性模型的学习算法，也是效果非常强大的，因此在工业界和学术界都非常常见。

最优化目标(Optimization Objective)

首先，我们回忆一下logistic regression：

根据样例的标签，我们希望模型能给出最接近标签的输出。比如如果样例的真实标签是1，我们希望LR模型能输出接近1的值，也等价于希望$\theta^Tx$的值能尽可能大。

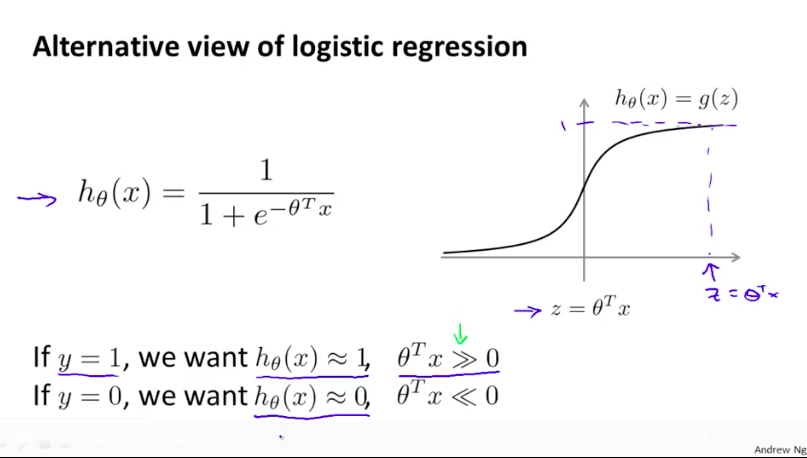
根据这个对于LR模型的期望，我们画出如下图的LR算法的损失函数（圆滑的蓝色细线）。然后，我们画出另外一个和LR算法的损失函数形状比较类似的新的损失函数曲线（紫色的细直线），这个新的损失函数曲线也是满足我们对于一个比较好的学习算法的期望的。

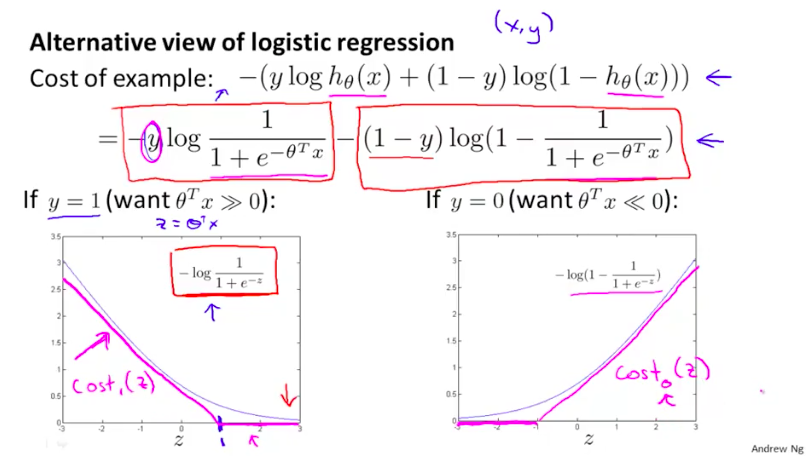
而这个新的损失函数曲线其实就是SVM算法的损失函数，我们将它们分别记为$cost_1(\theta^Tx)与cost_0(\theta^Tx)$，并写出SVM的成本函数+正则项：

另外，相对LR算法的成本函数，我们去掉了$\frac{1}{m}$的两项的公共乘积，并将原来的$A+\lamda B$的形式，写成了新的$CA+B$的形式，这对于优化过程所得最终的结果时没有影响的。

另外，和LR学到的假设不同，SVM所学到的假设也不会输出一个概率值，而是根据$\theta^Tx$的值与0的大小关系，输出0或1。

最大化边界的直觉（Large Margin Intuition）

我们再看一看SVM的损失函数，我们可能会希望在样例的真实标签为1时，$\theta^Tx$的值不止能大于等于0，最好能大于等于1，这样输出的结果就更趋向于真实的标签值（虽然是可能大于1，但是至少保证了输出值与真实标签值的距离，相对于错误的标签纸那边更近一些，即100与1的距离，肯定比于-1的距离要大一些）。

而当C取一个很大的值时，我们若要优化目标成本函数，那么就很需要使得与C相乘的的损失项的值的加和尽可能趋近于0.

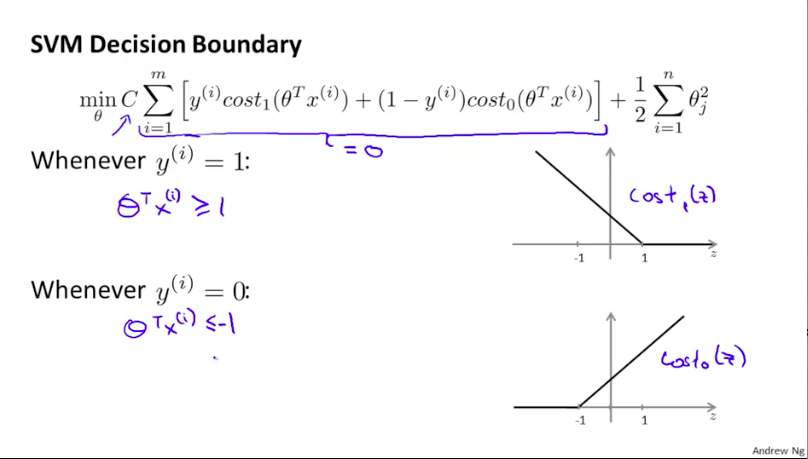
即我们的优化目标可以公式化表达为如下形式，

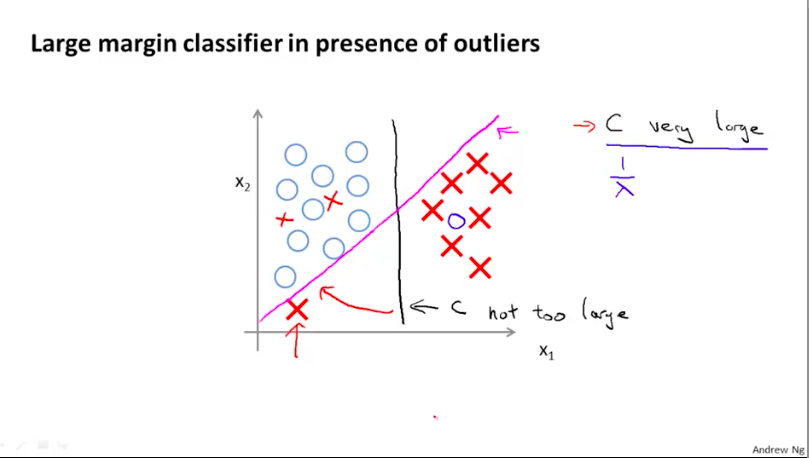
而从图像上来看，SVM的优化目标其实就是寻找下图中的那个黑线。黑线的特点是：它距离两类样例的最近点的边距（Margin）相等，并且这个边距是所有可以将两类样例正确划分开的直线的边距中最大的。这也是为什么SVM也被称为Large Margin Classifier。

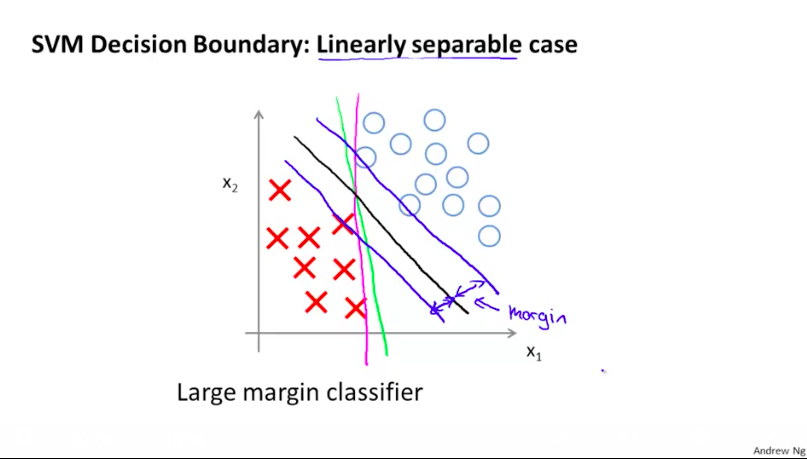
不过当有离群值（outlier）时，若C($\frac{1}{\lambda}$)也很大，就会使得SVM算法对离群值十分敏感，进而使得SVM学习到的分类曲线会为了离群值做很大的调整。相反，若C值不大，则不会因为离群值的存在，而造成分类曲线过大地调整。

最大化边界分类的数学原理(Mathematics Behind Large Margin Classification)

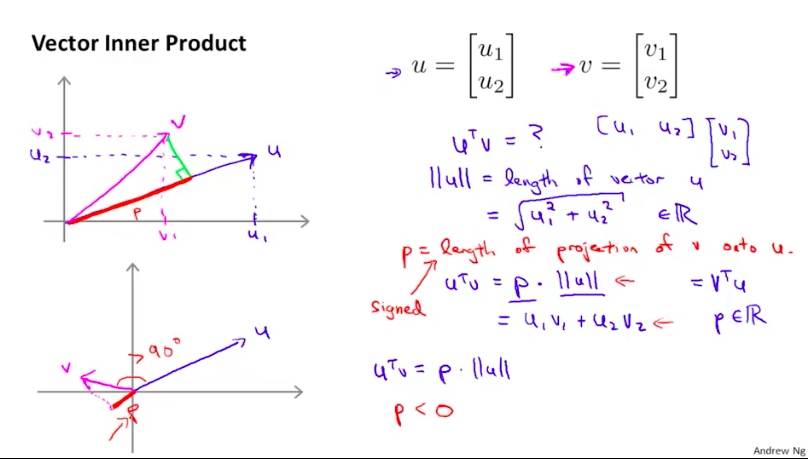
首先我们看一下向量u和向量v的内积的概念：向量u在向量v上投影（可为负值）与向量v的模长的乘积（也可以说成向量v在向量u上投影与向量u的模长的乘积），而这个值也等于向量u和向量v各分量的乘积的加和。

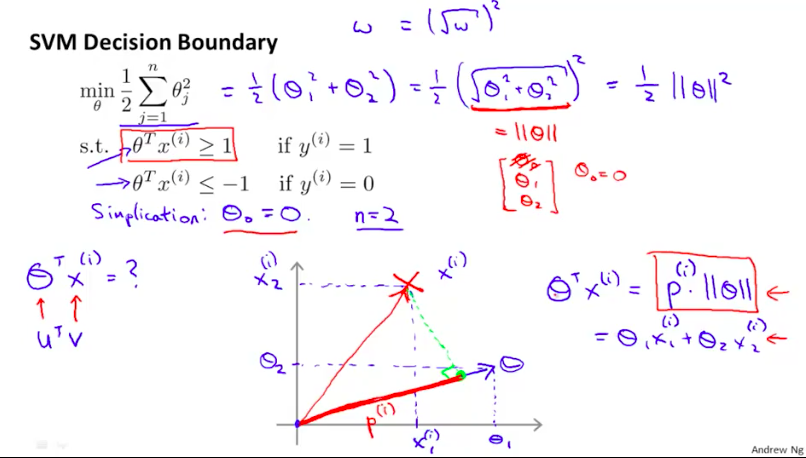
那么如下图，$\theta^Tx\ge 1$的限制条件也就可以用等价的$p^{(i)}*||\theta||$来替代。

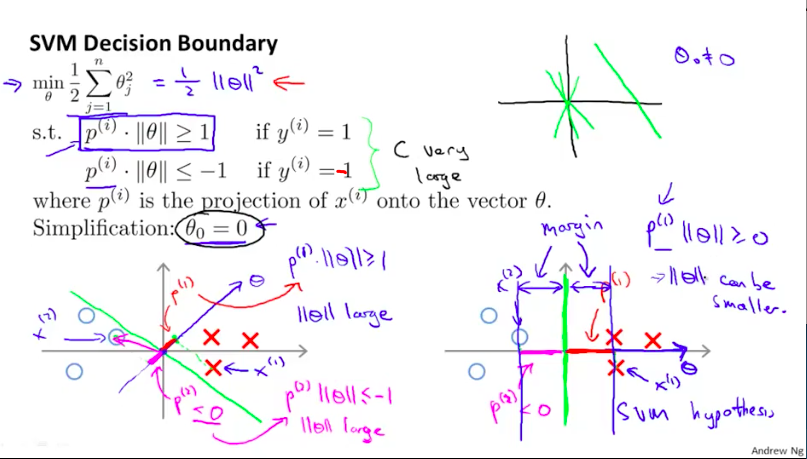
于是，根据下图，当我们的分类边界与样例的边距尽可能大时，$p^{(i)}$的值相对也就可以更大一些，而相对的，$\theta$的值就可以更小，这刚好符合我们的优化目标。

核（Kernel）

为了让SVM可以学习到强大的非线性分类器，我们需要用到核。

如下图是一个典型的非线性决策（分类）边界，这个边界使我们自己通过增加特征的二次项获得的：

那么，我们能不能让模型自己学习到这样的非线性边界呢？

我们首先将我们的新的目标学习特征$f_i$分别定义成原始特征向量与随机给定的$l^{(i)}$之间的similarity，similarity是由公式定义的两个向量之间的邻近程度：

那么，在这个情况下，similarity函数就是一个核函数（高斯核函数）。

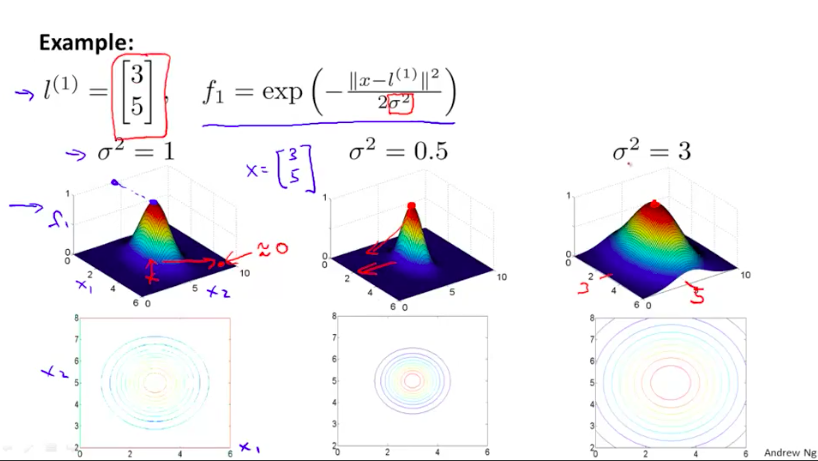
当原始特征向量x与$l^{(i)}$越相近，两者的similarity也就越接近于1，相反则接近于0。

同时如下图，根据$\alpha$参数值的不同，similarity的函数图像也在变化（$\alpha$越大，变化幅度越慢，反之则越快）

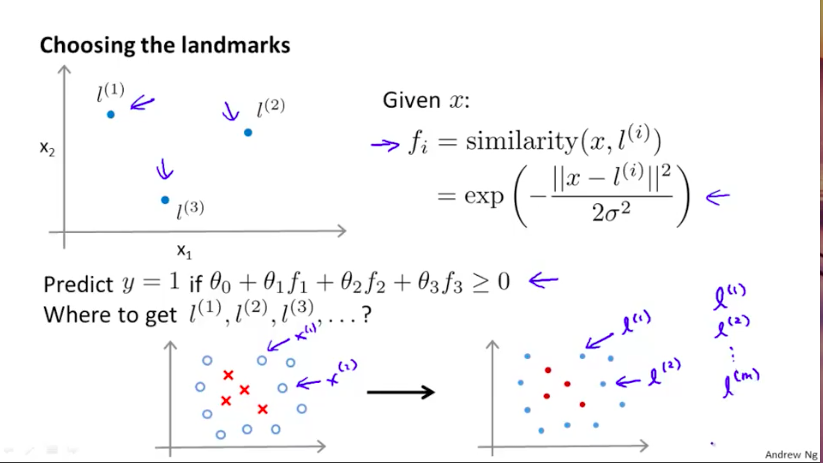
现在假设我们获得了参数$\theta_i$的值，那么我们会发现，距离$l^{(1)}与l$近的样例会比较被倾向于判断为正例，而距离$l^{(3)}$比较近的样例会比较被倾向于判断为负例。

那么问题来了，我们是如何确定$l^{(i)}$的呢？

我们会首先将训练集的m个样例全部分别作为最初的m个$l^{(i)}$，这样，每个样例x都能得到一个新的f系列特征。

那么我们的优化目标也就变成了如下形式：

在使用SVM的时候，我们需要选择的一个主要参数是C($\frac{1}{\lambda}$，$\lambda$是LR模型中的正则化参数)，它决定了我们学习到的假设是偏向于overfitting还是underfitting。另外还是参数$alpha$，

实际使用SVM的技巧

一般要具体制定的参数就是C和核函数。

使用线性核（不使用Kernel函数）时，不需要制定$\alpha$，而是用高斯核时就需要。

另外，在使用高斯核时，一定要对特征做scaling，否则f的值会很大程度上被取值范围更宽的特征值影响。

另外核函数的选择其实也很多：

另外，还有SVM做多分类的问题。其本质是用one-vs.-all方法，即训练出K个SVM，每一个SVM都被专门训练用于判断某个样本是否属于某个类，将这K个SVM学习到的假设组合起来，我们就能获得K个$\theta$参数，最后我们会为样例x判定为类i，以使得$(\theta^{(i)})Tx$最大。

还有在使用LR模型与SVM之间的抉择：

• 如果特征数目n很大（相对于样本容量m来说，比如n=10,000,m=10...1000），使用LR或者线性核的SVM即可。（没有足够的数据去拟合复杂的非线性函数）

• 如果特征数目n较小，样本容量m适中，比如n=1-1000,m=10-10000，使用高斯核SVM。

• 如果特征数目n较小，样本容量m很大，比如n=1-1000,m=50,000+，则增加特征数，并使用LR模型或者线性核SVM。（数据量太大，跑高斯核SVM会速度很慢）