集成学习（Ensemble Learning）

本博客是针对周志华教授所著《机器学习》的“第8章 集成学习”部分内容的学习笔记。

---

目录

• 个体与集成
• Boosting
• Bagging与随机森林
  • Bagging
  • 随机森林
• 结合策略
  • 平均法
  • 投票法
  • 学习法

个体与集成

集成学习，顾名思义，通过将多个单个学习器集成/组合在一起，使它们共同完成学习任务，有时也被称为“多分类器系统（multi-classifier system）”、基于委员会的学习（Committee-based learning）。

这里的【学习器】就是指机器学习算法训练得到的假设。而我们之所以有直觉要把多个学习器组合在一起，是因为单个学习器往往可能效果不那么好，而多个学习器可以互相帮助，各取所长，就可能一起合作把一个学习任务完成得比较漂亮。（后面我们将从数学上证明这一点）

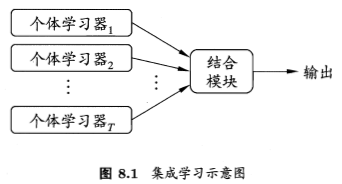
如下图，集成学习的一般结构是：先产生一组“个体学习器”（individual learner），再用某种策略将它们结合起来。

个体学习器通常是用一个现有的学习算法从训练数据产生，例如C4.5决策树算法、BP神经网络算法等。此时集成中只包含同种类型的个体学习器，例如“决策树集成”中的个体学习器全是决策树，“神经网络集成”中就全是神经网络，这样的集成是“同质”（homogeneous）的，同质集成中的个体学习器也称为“基学习器”（base learner），相应的学习算法称为“基学习算法”（base learning algorithm）。有同质就有异质（heterogeneous），若集成包含不同类型的个体学习器，例如同时包含决策树和神经网络，那么这时个体学习器一般不称为基学习器，而称作“组件学习器”（component leaner）或直接称为个体学习器。

• 弱学习器（weak learner）

  弱学习器常指泛化性能略优于随机猜测的学习器：例如在二分类问题桑精度略高于50%的分类器。

前面提到，集成学习的直觉是结合多个个体的能力，获得远超个体的集体能力优势。这种直觉在实际上对于“弱学习器”是非常符合的。故很多集成学习的研究也都是针对弱学习器，而基学习器有时也被直接成为弱学习器。

• 确实有效的集成？

一般经验中，如果把好坏不一的东西掺杂在一起，那么最终结果很可能是整体效果比最坏的东西要好一些，但又比最好的那个要坏一些，那么这种情况下不如就让最好的单独去工作，而不要参与混合。但是集成学习还是对多个学习器进行了结合，那它怎么保证整体的效果会比最好的那个单一学习器的效果更好呢。

用一个简单的例子来进行说明：在一个二分类任务重，假设三个分类器在三个测试样本上的表现如下图所示。假设集成学习的结果通过三个个体学习器用投票发（voting）产生，即“少数服从多数”，那么当三个个体学习器分别对三个测试例有不同的判别优势时，集成的效果也会不一样。

在（a）图中，每个分类器原本只有66.6%的精度，集成学习却达到了100%；（b）图中，每个分类器都是一样的，集成之后性能没有任何提高；在（c）图中，每个分类器的精度只有33.3%，集成之后结果反而变得更糟。

这个例子表明：要获得好的集成，个体学习器应“好而不同”，即个体学习器要有一定的准确性，即学习器不能太坏，并且要有“多样性”（diversity），即学习器间具有差异。

• 简单的数理分析

假设有一个二分类问题，其中$y\in{-1,+1}$，以及真实函数f，假定及分类器的错误率为$\epsilon$，即对于每个基分类器$h_i$有：
$$P(h_i(x)\neq f(x))=\epsilon。$$
假设集成通过简单投票法结合T（为简化讨论，假设T为奇数）个基分类器，若有超过半数的基分类器正确，则集成分类就正确：
$$H(x)=sign(\Sigma_{i=1}^T h_i(x)。$$
假设基分类器的错误率相互独立，则由Hoeffding不等式可知，集成的错误率为：
$$P(H(x)\neq f(x))=\Sigma_{k=1}^{[T/2]}C_Tk(1-\epsilon)^k\epsilon\le exp(-\frac{1}{2}T(1-2\epsilon)^2)。$$

上式表明，随着集成个体分类器数目T的增大，集成的错误率将指数级下降，最终趋向于0。

上述式子的推导是基于一个关键假设：基学习器的误差相互独立。然而现实情况是，个体学习器都是为解决同一个问题训练出来的，它们之间显然不可能相互独立。而事实上，个体学习器的“准确性”和“多样性”本身就存在冲突。一般的，准确性很高之后，要增加多样性就需牺牲准确性。而如何产生并结合“好而不同”的个体学习器，恰是集成学习研究的核心。

而根据个体学习器生成方式的不同，目前集成学习方法大致可分为两大类，即个体学习器间存在强依赖关系、必须串行生成的序列化方法，以及个体学习器间不存在强依赖关系、可同时生成的并行化方法；前者的代表是Boosting，后者的代表是和Bagging和“随机森林”（Random Forest）。

Boosting

Boosting是一族可将弱学习器提升为强学习器的算法。这一族算法的工作机制都是类似的：先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直至基学习器数目达到事先指定的值T，最终将这T个基学习器进行加权结合。

Boosting族算法最著名的代表是AdaBoost，它的算法描述如下图，其中$y_i\in {-1,+1}$,f是真实函数。

AdaBoost算法有多种推到方式，比较容易理解的是基于“加性模型”（additive model），即基学习器的线性组合
$$H(x)=\Sigma_{t=1}^T\alpha_th_t(x)$$
来最小化指数损失函数
$$l_{exp}(H|D)=E_{x\sim D[e^{-f(x)H(x)}]}。$$

推导过程不具体描述，贴出书上的过程

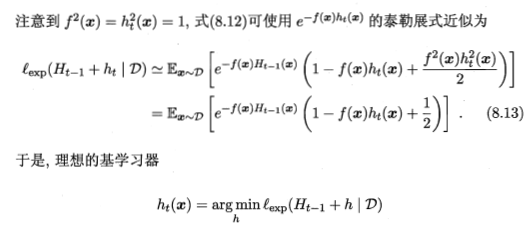
Boosting算法要求基学习器对特定的数据分布进行学习，这一点是通过“重赋权法”（re-weighting）实现的，即在训练过程的每一轮中，根据样本分布为每个训练样本重新赋予一个权重，对无法接受代全样本的基学习算法，则可通过“重采样法”（re-sampling）来处理，即在每一轮学习中，根据样本分布对训练集重新进行采样，再用重采样而得到的样本集对基学习器进行训练。一般而言，这两种做法没有显著的优劣差别。不过由于Boosting算法在训练的每一轮都会检查当前生成的基学习器的性能是否比随机猜测好，若不符合则抛弃当前基学习器，并停止学习过程，这会导致最后的集成中只包含很少的基学习器而性能不佳。而若采用“重采样阀”，则可以获得“重启动”机会以避免训练过程的过早停止，即在抛弃不满足条件的当前基学习器之后，再根据当前分布重新对训练样本进行重采样，再基于新的采样结果重新训练出基学习器，从而使得学习过程可以持续到预设的T轮完成。

而从偏差-方差分解的角度看，Boosting主要关注降低偏差（避免欠拟合），因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成。我们以决策树桩为基学习器，在西瓜数据集3.0$\alpha$上运行AdaBoost算法，不同规模（size）的集成及其基学习器所对应的分类边界如下图所示：

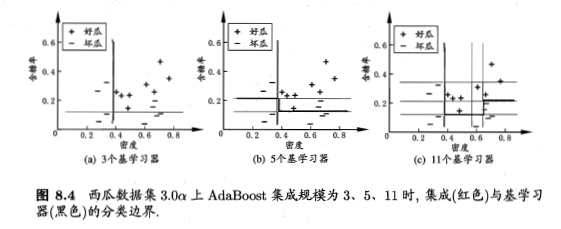
Bagging与随机森林

由第一部分内容可知，要想获得泛化性能强的集成，集成中的个体学习器应尽可能相互独立。而“独立”在现实任务中比较难以做到，不过我们可以设法使基学习器尽可能具有较大的差异。给定一个训练集，一种可能的做法是对训练样本进行采样，产生出若干个不同的子集，再从每个数据子集中训练出一个基学习器，这样，由于训练数据不同，我们获得的基学习器可望具有比较大的差异。然而，为获得好的集成，我们同时希望个体学习器不能太差。如果采样出的每个子集都完全不同，则每个基学习器只用到了一小部分训练数据，那甚至不能进行有效的学习，更不谈确保产生比较好的基学习器了。于是，为了解决这个问题，我们使用相互有交叠的采样子集。

Bagging

Bagging基于前面提到过的自助采样法（bootstrap sampling）。给定包含m个样本的数据集，我们先随机取出一个样本放入采样集中，再把该样本放回初始数据集，使得下次采样时该样本仍有可能被选中，这样，经过m此随机采样操作，我们得到含m个样本的采样集，初始训练集中有的样本在采样集里多次出现，有的则从未出现。由书之前的推导（式(2.1)）可知，初始训练集中越有63.2%的样本出现在采样集中。

于是，我们可以采样出T个含m个训练样本的采样集，然后基于每个采样集训练出一个基学习器，再集成，这就是Bagging的基本流程。在对预测输出进行结合时，Bagging通常对分类任务采用简单投票法，对回归任务使用简单平均法。若分类预测时出现两个类收到同样票数的情形，则最简单的做法是随机选择一个，也可进一步考察学习器投票的置信度来确定最终胜者。

Bagging的算法描述如下图：

• 包外估计（out-of-bag estimate）

Bagging的自助采样做法为Bagging带来一个优点是：由于每个基学习器只使用了初始训练集中大约63.2%的样本，剩下的约36.8%的样本则可用作验证集来对泛化性能进行“包外估计”。为此，需记录每个基学习器所使用的训练样本，不妨令$D_t$表示$h_t$实际使用的训练样本集，令$H^{oob}(x)$表示对样本x的包外预测，即仅考虑那些未使用x训练的基学习器在x上的预测，有：
$$H^{oob}(x)=arg\ max_{y\in Y}\Sigma_{t=1}^TII(h_t(x)=y)\cdot II(x\notin D_t)$$
则Bagging泛化误差的包外估计为
$$\epsilon^{oob}=\frac{1}{|D|}\Sigma_{(x,y)\in D}II(H^{oob}(x)\ne y)$$

从偏差-方差分解的角度看，Bagging主要关注降低方差（防止过拟合），因此它在不剪枝决策树、神经网络等容易受样本扰动的学习器上效用更为明显。

随机森林

随机森林（Random Forest，简称RF）是Bagging的一个扩展变体。其在以决策树作为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择。

具体来说，传统决策树在选择划分属性时是在当前结点的属性集合（假定有d个属性）中选择一个最有属性；而在RF中，对基决策树的每个结点，先从该结点的属性集合中随机选择一个包含k个属性的子集，然后再从这个子集中选择一个最优属性用于划分。这里的参数k控制了随机性的引入程度：若令k=d，则基决策树的构建与传统决策树相同；若令k=1，则是随机选择一个属性用于划分；一般情况下，推荐值k=$log_2d$。

RF简单、容易实现、计算开销小，而令人惊奇的是，它在很多学习任务中展现出强大的性能，被誉为“代表集成学习技术水平的方法”。

RF的收敛性与Bagging相似。如下图所示，随机森林的起始性能往往相对较差，特别是在集成中只包含一个基学习器时，这很容易理解，因为通过引入属性扰动，随机森林中个体学习器的性能往往有所降低。然而，随着个体学习器数目的增加，随机森林通常会收敛到更低的泛化误差。

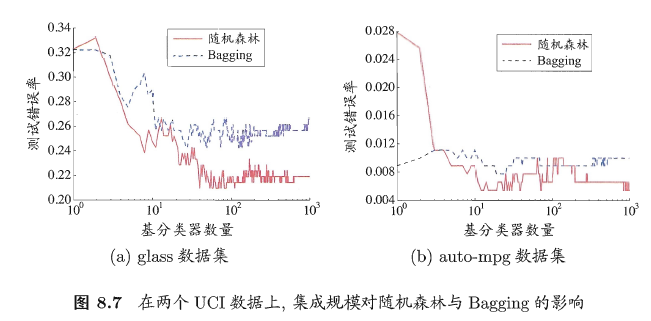
结合策略

假设集成中包含T个基学习器${h_1,h_2,...,h_T}$，其中$h_i$在示例x上的输出为$h_i(x)$。那么对$h_i$进行结合的常见策略有以下几种：

平均法

平均法主要针对回归类任务。

对数值型输出$h_i(x)\in R$，最常见的结合策略是平均法（averaging）。

• 简单平均法（ averaging）
  $$H(x)=\frac{1}{T}\Sigma_{i=1}^Th_i(x)。$$

• 加权平均法
  $$H(x)=\Sigma_{i=1}^Tw_ih_i(x)，$$
  这里$w_i$表示个体学习器$h_i$的权重，通常要求$w_i\ge 0,\Sigma_{i=1}^Tw_i=1。$

加权平均法的权重一般是从训练数据中学习而得，现实任务中的训练样本通常不充分或存在噪声，这将使得学出的权重不完全可靠。因此，实验和应用均显示出，加权平均分未必一定优于朴素的简单平均法。一般而言，在个体学习器的性能相差较大时宜使用加权平均法，而在个体学习器性能相近时宜使用简单平均法。

投票法

投票法主要针对分类任务。

对分类任务来说，学习器$h_i$将从类别标记集合${c_1,c_2,...,c_N}$中预测出一个标记，最常见的结合策略是使用投票法。为便于讨论，我们将$h_i$在样本x上的预测输出表示为一个N维向量(h_i^1(x);h_i2(x);...;h_i^{N(x))，其中$h_i}j(x)$是$h_i$在类别标记$c_j$上的输出。

• 绝对多数投票法（ majority voting）

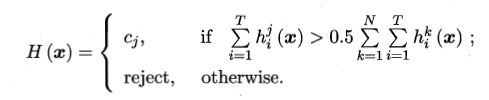
• 相对多数投票法（plurality voting）

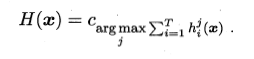
• 加权投票法（weighted voting）

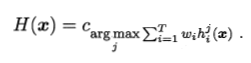
学习法

当训练数据很多时，一种更为强大的结合策略是使用“学习法”，即通过另一个学习器来进行结合。Stacking是学习法的典型代表，这里我们把个体学习器称为初级学习器，用于结合的学习器称为次级或者元学习器。

Stacking先从初始训练集训练出初级学习器，然后“生成”一个新数据集用于训练次级学习器。在这个新数据集中，初级学习器的输出被当作样例输入特征，而初始样本的标记仍被当做样例标记。Stacking的算法描述如下图所示，这里假定初始学习器使用不同学习算法产生（例如可同时包含决策树，神经网络算法），即初级集成是异质的。