Leetcode——二叉树常考算法整理
2018-05-28 16:43 bluemapleman 阅读(310) 评论(0) 收藏 举报二叉树常考算法整理
希望通过写下来自己学习历程的方式帮助自己加深对知识的理解,也帮助其他人更好地学习,少走弯路。也欢迎大家来给我的Github的Leetcode算法项目点star呀~~
前言
二叉树即子节点数目不超过两个的树,基于这个基本特性,许多算法都围绕这种树本身或其变体而展开。
二叉树的类型
此部分参考一句话弄懂常见二叉树类型
根据树的构成特性,树存在一些比较常见的类型,我们先来分别介绍一下:
- 满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。
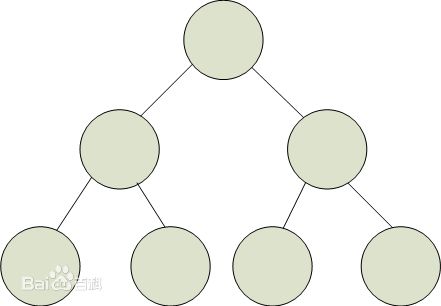
- 完全二叉树
一棵二叉树至多只有最下面的一层上的结点的度数可以小于2,并且最下层上的结点都集中在该层最左边的若干位置上,则此二叉树成为完全二叉树。
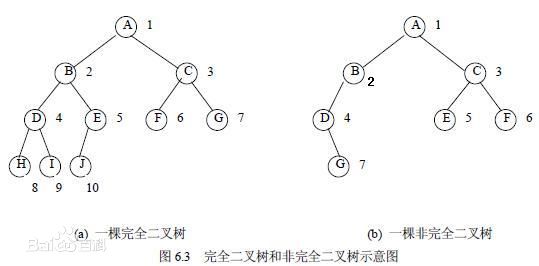
- 平衡二叉树
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
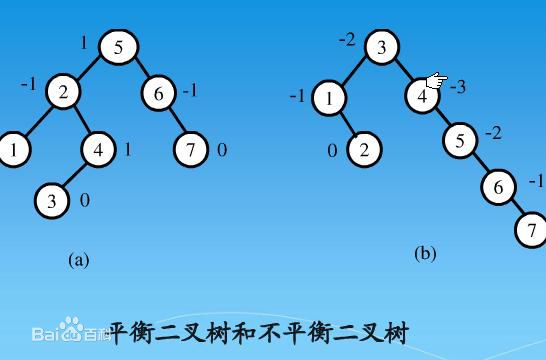
- 二叉搜索/查找/排序树
它或者是一棵空树,或者是具有下列性质的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
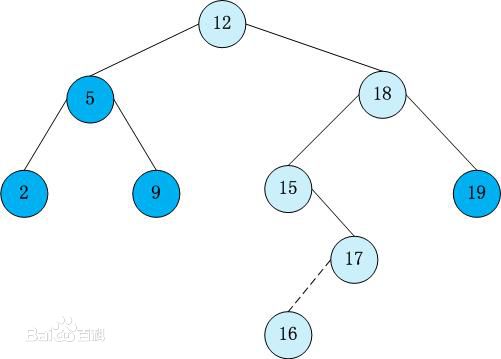
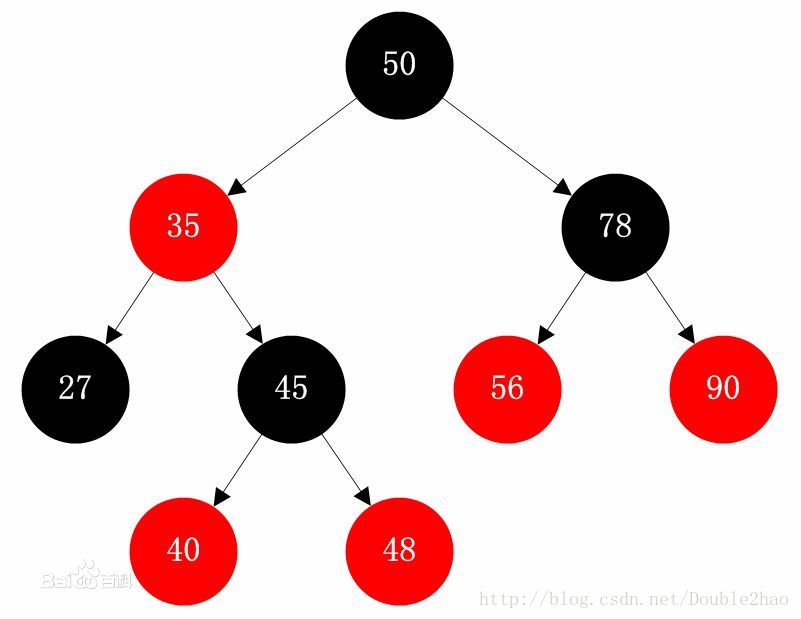
- 红黑树
属于AVL树(平衡二叉查找树)的一种,对树的高度的要求不如AVL树那么严格(不是严格控制左、右子树高度或节点数之差小于等于1),使得其插入结点的效率相对更高。
算法分类
遍历(Traversal)问题
先序、中序与后序遍历
对任一二叉树结点,若以其本身为根结点(Root Node),它的左右子节点(left/right child),那么遍历指的就是以某种固定顺序将整个二叉树的所有结点都过一遍。
按照根节点与子节点先后遍历关系,一共有以下三种常见的遍历顺序:
- 先序遍历(Preorder)
根结点-左子结点-右子结点
- 中序遍历(Inorder)
左子结点-根结点-右子结点
- 后序遍历(Postorder)
左子结点-右子结点-根结点
遍历,根据实现思路,可以分为递归(Recursive)和非递归两种方式。递归相对来说更为直观易理解,但是由于递归需要不断地多重地进行函数自身调用,会需要消耗更多的栈空间。而非递归方式就是用一般的循环(Iteration)来进行。(而其实由于二叉树的结构特性,许多相关的题目的解题思路都会存在递归和非递归两种方式,只要多做几道,就会自然体味到其中的规律。)
先给出递归实现的三种遍历:
/*
* 递归的主要思想就是:
* 由于是重复调用自身,故根据遍历顺序调整根节点与左右子节点的处理语句之间的相对顺序即可。
*/
//递归先序遍历
public static void recurivePreorder(TreeNode root){
if(root==null)
return;
System.out.println(root.val);
if(root.left!=null)
recurivePreorder(root.left);
if(root.right!=null)
recurivePreorder(root.right);
}
//递归中序遍历
public static void recursiveInorder(TreeNode root){
if(root==null)
return;
if(root.left!=null)
recursiveInorder(root.left);
System.out.println(root.val);
if(root.right!=null)
recursiveInorder(root.right);
}
//递归后序遍历
public static void recursivePostorder(TreeNode root){
if(root==null)
return;
if(root.left!=null)
recursivePostorder(root.left);
if(root.right!=null)
recursivePostorder(root.right);
System.out.println(root.val);
}非递归实现三种遍历:
/*
* 非递归的主要思想是:
* 利用栈stack存下路过的结点,依照遍历顺序打印结点,利用stack回溯。
*/
//非递归先序遍历
public static void nonRecurPreorder(TreeNode root){
ArrayDeque<TreeNode> stack=new ArrayDeque<TreeNode>();
while(root!=null || stack.size()!=0){
if (root != null) {
System.out.println(root.val); //访问结点并入栈
stack.push(root);
root = root.left; //访问左子树
} else {
root = stack.pop(); //回溯至父亲结点
root = root.right; //访问右子树
}
}
}
//非递归中序遍历
public static void nonRecurInorder(TreeNode root){
ArrayDeque<TreeNode> stack=new ArrayDeque<TreeNode>();
while(root!=null || stack.size()!=0){
if(root!=null){
stack.push(root);
root=root.left; //访问左子树
}
else{
root=stack.pop(); //回溯至父亲结点
System.out.println(root.val); //输出父亲结点
root=root.right; //访问右子树
}
}
}
//非递归后序遍历(相对来说,是二叉树遍历中最为复杂的一种)
// 思路:如果当前结点没有左右子树,或者左右子树均已被访问过,那么就直接访问它;否则,将其右孩子和左孩子依次入栈。
public static void nonRecurPostorder(TreeNode root){
ArrayDeque<TreeNode> stack=new ArrayDeque<TreeNode>();
TreeNode pre=null;
TreeNode cur=null;
stack.push(root);
while(stack.size()!=0){
cur=stack.peek();
if((cur.left==null && cur.right==null) || (pre!=null && (pre==cur.left || pre==cur.right))){
System.out.println(cur.val); //输出父亲结点
pre=cur;
stack.pop();
}
else{
if(cur.right!=null)
stack.push(cur.right);
if(cur.left!=null)
stack.push(cur.left);
}
}
}利用两种遍历结果构造二叉树
上面讲到,二叉树的遍历方式一般分为先序、中序和后序三种,其中先序和中序,或者中序和后续的遍历的结果就可以确定第三种的遍历结果,也即确定了一棵具体的二叉树。(此处默认二叉树无值相同的两个结点)
- 利用先序与中序构造二叉树
(此处,我们仅对这道题进行细致分析,另两道题目是一模一样的思路。)
先序代表了父亲-左孩子-右孩子的顺序,中序代表了左孩子-父亲-右孩子的顺序,因此,从遍历序列的整体来看,先序序列的第一个结点代表的就是整棵树的根结点,而我们在中序序列中定位到这个结点后,中序序列这个结点以左的结点就是根结点左子树上的所有结点,这个结点以右的结点就是根结点右子树上的所有结点。然后我们将先序序列按照由中序序列那里得知的划分,找到左右子树的划分边界。以此类推,我们就可以通过不断地交替从两个序列中获得构造二叉树所需要的所有信息。
原题:LC105 Construct Binary Tree from Preorder and Inorder Traversal
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder.length==0)
return null;
TreeNode root=new TreeNode(preorder[0]);
if(preorder.length==1)
return root;
int leftSubTreeNodeNums=-1;
for(int i=0;i<inorder.length;i++)
if(inorder[i]==root.val) {
leftSubTreeNodeNums=i;
break;
}
root.left=buildTree(Arrays.copyOfRange(preorder, 1, leftSubTreeNodeNums+1), Arrays.copyOfRange(inorder,0,leftSubTreeNodeNums));
root.right=buildTree(Arrays.copyOfRange(preorder, leftSubTreeNodeNums+1, preorder.length), Arrays.copyOfRange(inorder,leftSubTreeNodeNums+1,inorder.length));
return root;
}- 利用中序与后序构造二叉树
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(inorder.length==0)
return null;
if(inorder.length==1)
return new TreeNode(inorder[0]);
TreeNode root=new TreeNode(postorder[postorder.length-1]);
int leftTreeNodeSum=0;
for(int i=0;i<inorder.length;i++)
if(inorder[i]==root.val){
leftTreeNodeSum=i;
break;
}
root.left=buildTree(Arrays.copyOfRange(inorder, 0, leftTreeNodeSum), Arrays.copyOfRange(postorder, 0, leftTreeNodeSum));
root.right=buildTree(Arrays.copyOfRange(inorder, leftTreeNodeSum+1, inorder.length), Arrays.copyOfRange(postorder, leftTreeNodeSum, postorder.length-1));
return root;
}递归问题
递归解二叉树问题时,一般以一棵三结点或更多结点的小树作为思考解法的参照物,然后考虑一下递归的返回情况(一般是碰到空结点的时候)如何处理。
二叉树最大深度
原题:LC104 Maximum Depth of Binary Tree
Given a binary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Note: A leaf is a node with no children.
Example:
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7return its depth = 3.
- My Answer
// 思路:典型的递归思路,整颗树的最大深度等于左右子树的最大深度+1。
public int maxDepth(TreeNode root) {
if(root==null)
return 0;
else
return 1+Math.max(maxDepth(root.left),maxDepth(root.right));
}二叉树最小深度
原题:LC111 Minimum Depth of Binary Tree
Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
Note: A leaf is a node with no children.
Example:
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7return its minimum depth = 2.
- My Answer
// 思路:根据左右孩子的不同情况分别返回不同的相应深度,在左右孩子均存在时,返回深度较小的那一边,以获得最小深度。
public int minDepth(TreeNode root) {
if(root==null)
return 0;
else if(root.left==null && root.right==null)
return 1;
else if(root.left!=null && root.right!=null)
return 1+Math.min(minDepth(root.left), minDepth(root.right));
else
if(root.left!=null)
return 1+minDepth(root.left);
else
return 1+minDepth(root.right);
}平衡二叉树判断
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
Example 1:
Given the following tree [3,9,20,null,null,15,7]:
3
/ \
9 20
/ \
15 7Return true.
Example 2:
Given the following tree [1,2,2,3,3,null,null,4,4]:
1
/ \
2 2
/ \
3 3
/ \
4 4Return false.
- My Answer
//思路:判断整棵树是否为平衡二叉树,等价于判断根节点的左右子树的高度差是否小于等于1,且左右子树是否也都为平衡二叉树。
// 而判断高度差的方法可以利用前面求二叉树最大深度的方法,去分别算出左右子树的高度作差。
public static boolean isBalanced(TreeNode root) {
if(root==null)
return true;
else {
if(Math.abs(getMaxTreeDepth(root.left)-getMaxTreeDepth(root.right))<=1){
return isBalanced(root.left) && isBalanced(root.right);
}else {
return false;
}
}
}
public static int getMaxTreeDepth(TreeNode root) {
if(root==null)
return 0;
else
return 1+Math.max(getMaxTreeDepth(root.left),getMaxTreeDepth(root.right));
}相同树
Given two binary trees, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical and the nodes have the same value.
Example 1:
Input: 1 1
/ \ / \
2 3 2 3
[1,2,3], [1,2,3]
Output: trueExample 2:
Input: 1 1
/ \
2 2
[1,2], [1,null,2]
Output: falseExample 3:
Input: 1 1
/ \ / \
2 1 1 2
[1,2,1], [1,1,2]
Output: false- My Answer
// 思路:逐结点判断,若每个结点都相同,那么整棵树就相同。
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p==null && q==null) {
return true;
}
else if(p!=null && q!=null){
if(p.val==q.val)
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
else
return false;
}
else
return false;
}对称树
Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).
For example, this binary tree [1,2,2,3,4,4,3] is symmetric:
1
/ \
2 2
/ \ / \
3 4 4 3But the following [1,2,2,null,3,null,3] is not:
1
/ \
2 2
\ \
3 3Note:
Bonus points if you could solve it both recursively and iteratively.
- My Answer
// 思路:判断对称树即判断左右子树镜面对称位置的结点是否均存在,且值相同。
public boolean isSymmetric(TreeNode root) {
return isMirror(root,root);
}
public boolean isMirror(TreeNode t1, TreeNode t2) {
if (t1 == null && t2 == null) return true;
if (t1 == null || t2 == null) return false;
return (t1.val == t2.val)
&& isMirror(t1.right, t2.left)
&& isMirror(t1.left, t2.right);
}路径总和
Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.
Note: A leaf is a node with no children.
Example:
Given the below binary tree and sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.
- My Answer
// 思路:注意题意是找一条“从根节点到叶子结点”的路径和,所以到每一个结点判断是否值对的同时,还要判断是否没有孩子结点,如果有,还需要继续往下找。
public boolean hasPathSum(TreeNode root, int sum) {
if(root==null)
return false;
if(root.val==sum && root.left==null && root.right==null)
return true;
int goal=sum-root.val;
return hasPathSum(root.left, goal) || hasPathSum(root.right, goal);
}二叉搜索树/排序树问题
二叉排序树的特点前面提到过,即对于任一树中结点,其左子树的结点的值均小于它,而右子树的结点的值均大于它。根据这个特性,也存在一系列相关的算法题。
而由于依然是二叉树,故也常见用递归思路解决搜索树相关的题目。
验证二叉搜索树
LC98 Validate Binary Search Tree
Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
Input:
2
/ \
1 3
Output: trueExample 2:
5
/ \
1 4
/ \
3 6
Output: falseExplanation: The input is: [5,1,4,null,null,3,6]. The root node’s value
is 5 but its right child’s value is 4.
- My Answer
// 思路:要保证左子树的结点值均小于父结点值,右子树的结点值均大于父结点值,可以分别在左右子树中搜索最大最小值的结点,如果它们的值已经符合和父结点的大小关系,那么就只需再继续判断左右子树是否也都是二叉搜索树即可。
public boolean isValidBST(TreeNode root) {
if(root==null)
return true;
if(root.left==null && root.right==null)
return true;
int leftMax=findMaxValInBST(root.left, Integer.MIN_VALUE),rightMin=findMinValInBST(root.right, Integer.MAX_VALUE);
if(root.val!=Integer.MIN_VALUE) {
if(leftMax>=root.val)
return false;
}
if(root.val!=Integer.MAX_VALUE) {
if(rightMin<=root.val)
return false;
}
if(root.left!=null && root.right==null)
return root.left.val<root.val && isValidBST(root.left);
if(root.left==null && root.right!=null)
return root.right.val>root.val && isValidBST(root.right);
return root.left.val<root.val && root.right.val>root.val && isValidBST(root.left) && isValidBST(root.right);
}
public int findMaxValInBST(TreeNode root,int maxVal) {
if(root==null)
return maxVal;
if(root.val>maxVal)
maxVal=root.val;
int leftMax=findMaxValInBST(root.left, maxVal),rightMax=findMaxValInBST(root.right, maxVal);
return leftMax>rightMax?leftMax:rightMax;
}
public int findMinValInBST(TreeNode root,int minVal) {
if(root==null)
return minVal;
if(root.val<minVal)
minVal=root.val;
int leftMin=findMinValInBST(root.left, minVal),rightMin=findMinValInBST(root.right, minVal);
return leftMin<rightMin?leftMin:rightMin;
}唯一二叉搜索树
LC96 Unique Binary Search Trees
Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n?
Example:
Input: 3
Output: 5
Explanation:
Given n = 3, there are a total of 5 unique BST's:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3- My Answer
// 思路:动态规划
// f(n)=sum(f(n-i)*f(i-1)) i=1,2,3...,n
// 对于从1到n的n个结点,构成二叉搜索树的所有情况可以以左右子树上结点的数目来进行划分。
// 例如左边0个结点+右边n-1个结点,左边1个结点+右边n-2个结点......,左边n-1个结点,右边0个结点。
// 一种情况的左右子树的构成情况相乘,不同情况的结果加总即得到最后的解。
public int numTrees(int n) {
int numTrees[]=new int[n+1];
numTrees[0]=1;numTrees[1]=1;
for(int i=2;i<=n;i++) {
for(int j=1;j<=i;j++) {
numTrees[i]+=numTrees[j-1]*numTrees[i-j];
}
}
return numTrees[n];
}最低的二叉树共同祖先
LC235 Lowest Common Ancestor of a Binary Search Tree
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants (where we allow a node to be a descendant of itself).”
Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]
_______6______
/ \
___2__ ___8__
/ \ / \
0 _4 7 9
/ \
3 5Example 1:
Input: root, p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.Example 2:
Input: root, p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.- My Answer
// 思路:根据结点p和q的值与父亲结点值的大小关系判断p与q是否位于同一子树下,如果是,那么递归调用方法,如果不是,那么当前父亲结点就是两者的最低共同祖先。
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(p==q || p.right==q || p.left==q)
return p;
else if(q.left==p || q.right==p)
return q;
// if two nodes p and q are in same sub tree, then we need to go into lower layer recursively.
if(root.val>p.val && root.val>q.val) {
return lowestCommonAncestor(root.left, p, q);
}else if (root.val<p.val && root.val<q.val) {
return lowestCommonAncestor(root.right, p, q);
// if p and q not in same sub tree, then root is the lowest common ancestor.
}else {
return root;
}
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号