高等数学·定积分与反常积分
定积分与反常积分
定积分
一、定积分概念
1.定义
定理:(线性)
注解:积分无小事
2.定积分存在的充分条件
3.定积分的几何意义
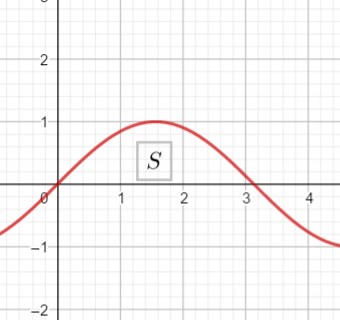
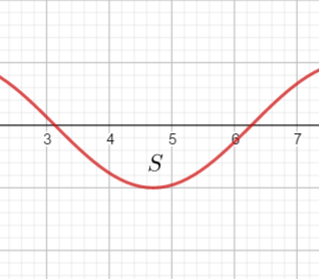
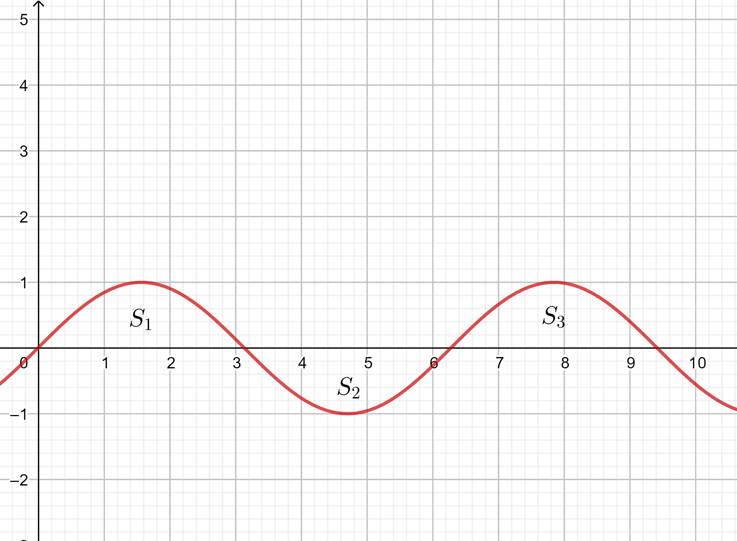
二、定积分的性质
1.不等式性质
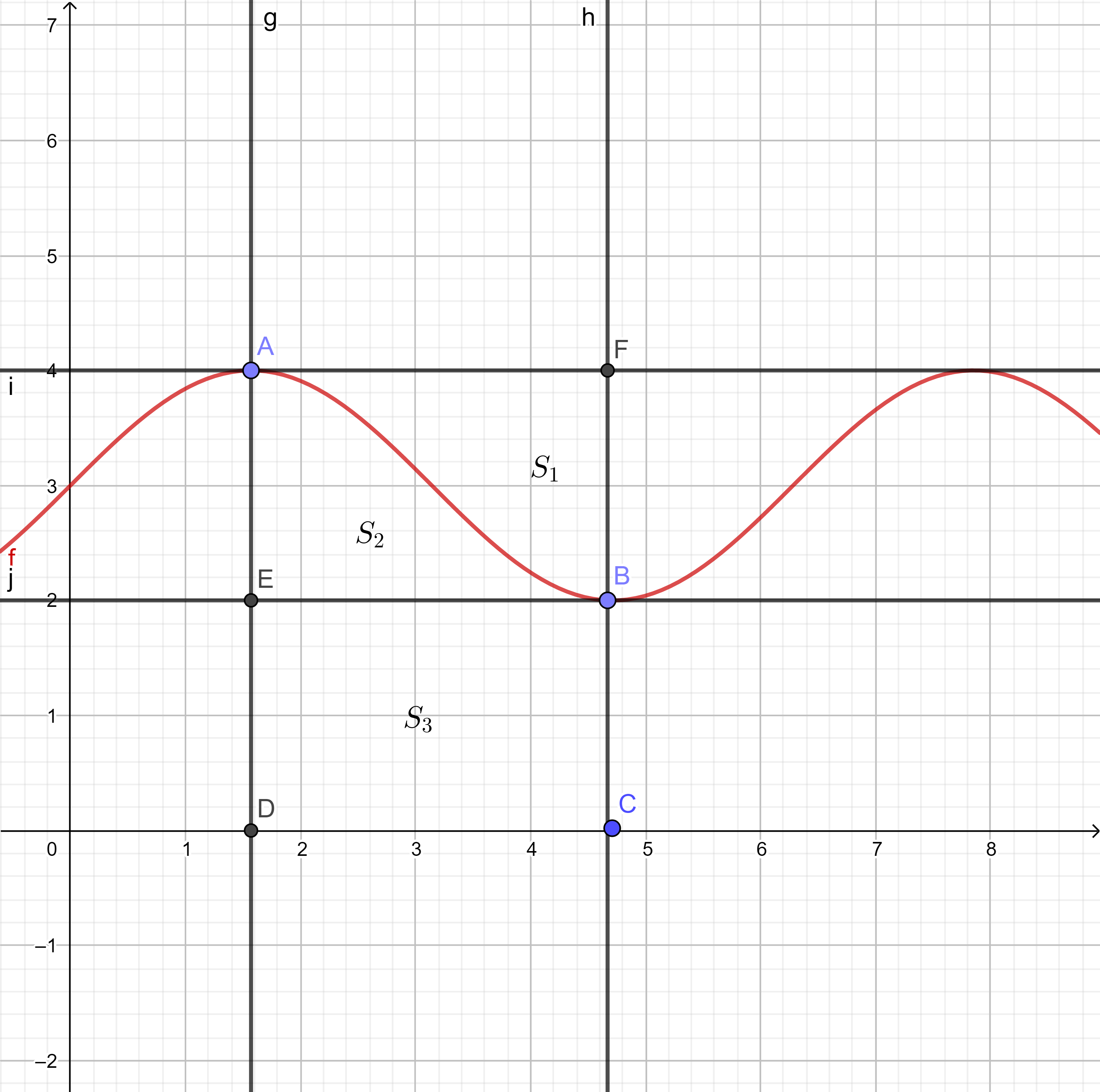
2.中值定理
三、积分上限函数
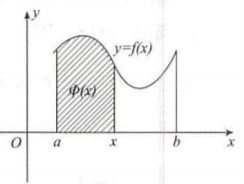
四、定积分的计算
1.牛顿莱布尼茨公式
2.换元积分法
3.分部积分法
4.奇偶性和周期性
5.已有公式
6.经典例题:
例题1:
例题2
例题3

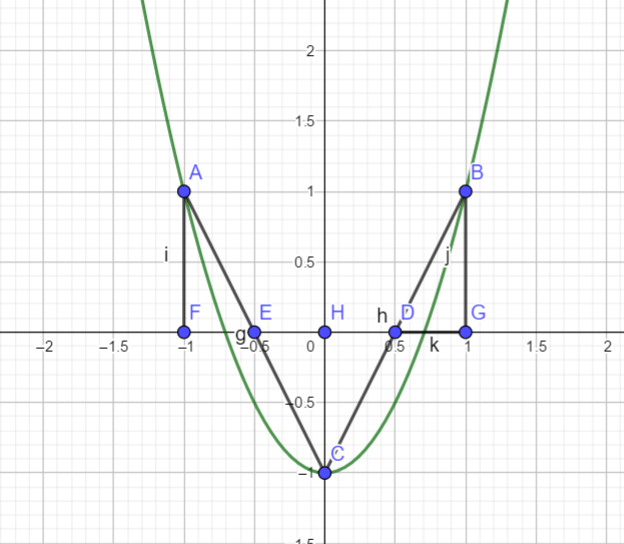
例题4
AZZK.jpg)
反常积分
一、无穷区间上的反常积分
二、无界函数的反常积分
三、例题
例题1
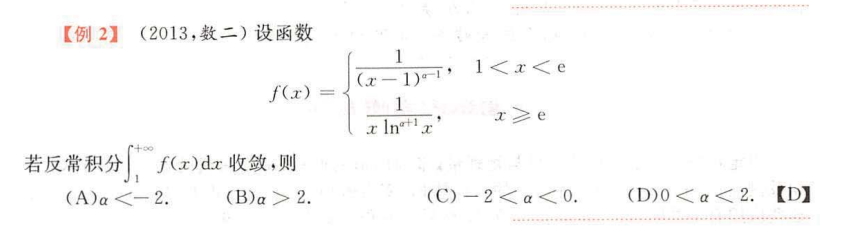
定积分的应用
一、几何应用
1.平面图形的面积
2.旋转体的体积
HIN4FCVUKI$%5DZB.jpg)
3.曲线弧长
4.旋转体侧面积
二、物理应用
1.压力
2.变力做功
3.引力(较少考)
例题1
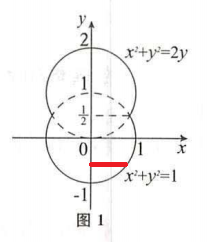
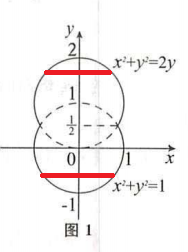
例题2
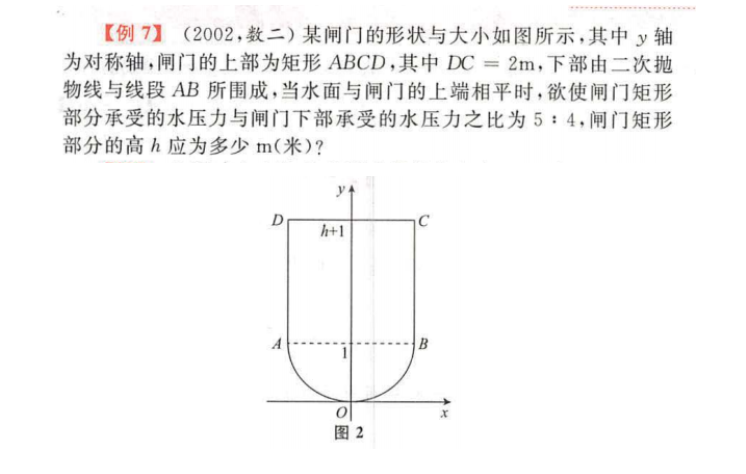
.jpg)





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 【杭电多校比赛记录】2025“钉耙编程”中国大学生算法设计春季联赛(1)