高等数学·导数与微分
导数与微分
(-)导数与微分概念
1.导数
\[\begin{aligned}
&定义1：(导数)(相当于x_0处的变化率)
f'(x_0)=\lim_{\Delta x\to 0} \tfrac{\Delta y}{\Delta x}=\lim_{\Delta x\to 0}\frac{f(x_0+x)-f(x_0)}{\Delta x}=\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}\\
&定义2：(左导数)(左领域内可导)\\
&f_-'(x_0)=\lim_{\Delta x\to 0^-} \tfrac{\Delta y}{\Delta x}=\lim_{\Delta x\to 0^-}\frac{f(x_0+x)-f(x_0)}{\Delta x}=\lim_{h\to 0^-}\frac{f(x_0+h)-f(x_0)}{h}\\
&定义2：(右导数)(右领域内可导)\\
&f_+'(x_0)=\lim_{\Delta x\to 0^+} \tfrac{\Delta y}{\Delta x}=\lim_{\Delta x\to 0^+}\frac{f(x_0+x)-f(x_0)}{\Delta x}=\lim_{h\to 0^+}\frac{f(x_0+h)-f(x_0)}{h}\\
\end{aligned}
\]
\[定理1：f'(x)可导\Leftrightarrow f'_-(x)\exist f'_+(x)\exist,f'_-(x)=f'_+(x)
\]
2.微分
\[\begin{align}
&定义4：(微分) 如果\Delta y=f(x_0+\Delta x)-f(x_0)可以表示为\\
&\Delta y=A\Delta x+o(\Delta x)\\
&则称函数f(x)在点x_0处可微,称A\Delta x为微分，记为dy=A\Delta x\\
&dy\approx \Delta y在一个微小的区域用均与的变量代替非均匀的变量\\
&微分是函数改变量的一个线性主部
\end{align}
\]
\[定理2：函数y=f(x)在点x_0处可微\Leftrightarrow f(x)在点x_0处可导，且有dy=f'(x_0)\Delta x=f'(x_0)dx
\]
\[\begin{align}
&S(x)=x^2,S(x+\Delta x)=(x+\Delta x)^2\\
&\Delta S=(x+\Delta x)^2-x^2=2x+(\Delta x)^2=2x+O(\Delta x)\\
&线性主部(ds=2x\Delta x=S'(x)\Delta x)+高阶无穷小\\
&\Delta S\approx2x-\Delta x(\Delta x\rightarrow 0)\\
&\\
&\Delta f(x)=A\Delta x+O(\Delta x)(x\rightarrow 0)\Leftrightarrow \lim_{\Delta x \rightarrow 0}\frac{\Delta x-A\Delta x}{\Delta x}=0\\
&(1)若\exist A,使得\lim_{\Delta x \rightarrow 0}\frac{\Delta f-A\Delta x}{\Delta x}\\
&(2)若f可微,则\lim_{\Delta x \rightarrow 0}\frac{\Delta f-f'(x)\Delta x}{\Delta x}=0\\
\end{align}
\]
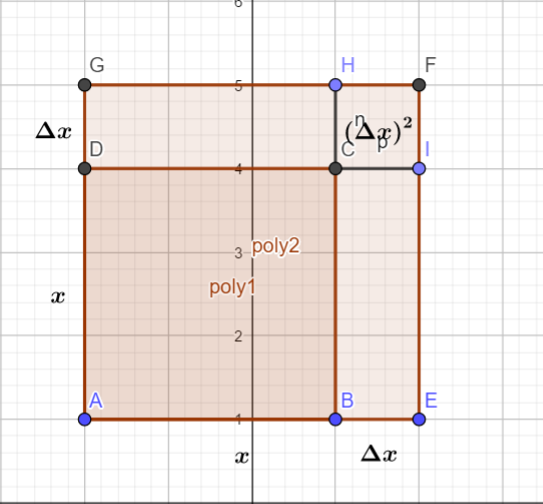
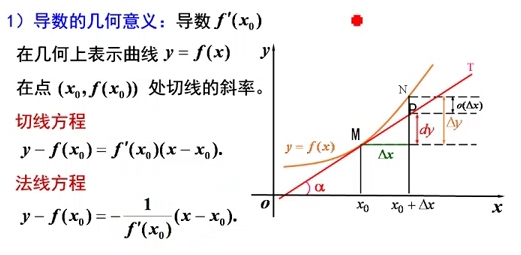
3.导数与微分的几何意义
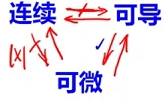
4.连续，可导，可微之间的关系
\[\begin{align}
&注解：f(x)在x_0处连续\Leftrightarrow \lim_{x\rightarrow x_0}f(x)=f(x_0)\\
&\Leftrightarrow \lim_{x\rightarrow x_0}[f(x)-f(x_0)]=0 即\lim_{\Delta x\rightarrow 0}\Delta f=0\\
\end{align}
\]
(二)导数公式及求导法则
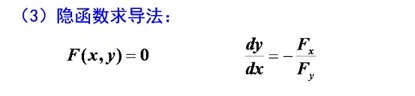
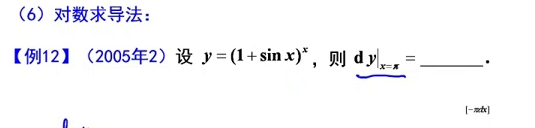
"乘除变加减"
\[u^v=e^{vln{u}}
\]
\[y=u^v \Leftrightarrow ln{y}=vln{u}
\]
高阶导数
\[\begin{align}
&设y=Sin3x,求y^{(n)}\\
&y'=Cos3x*3=Sin(3x+\frac{\pi}{2})*3\\
&y''=Cos(3x+\frac{\pi}{2})*3^2=Sin(3x+2*\frac{\pi}{2})\\
&\Rightarrow y^{(n)}=Sin(3x+n*\frac{\pi}{2})*3^n\\
&y=Sin(ax+b) \Rightarrow y^{(n)}=Sin(3x+n*\frac{\pi}{2})*3^n
\end{align}
\]
\[\begin{align}
&设y=x^2Cosx,求y^{(n)}\\
&令u=x^2,v=cosx\\
&u'=2x,u''=2,u'''=0,...u^{(n)}=0\\
&(uv)^{(n)}=\sum_{k=0}^{n}u^{k}v^{(n-k)}\\
&y^{(n)}=C_{n}^{0}x^2Cos(x+n*\frac{\pi}{2})+C_{n}^1(2x)Cos(x+(n-1)\frac{\pi}{2})+C^2_{n}(2)Cos(x+(n-2)*\frac{\pi}{2})
\end{align}
\]
(三)微分法
1.复合函数与初等函数的微分法
(1).基本微分
.jpg)
(2).复合函数微分法（链式法则）
\[\begin{align}
&设函数u=\Phi(x)于点x处可导,函数y=f(u)于点u=\Phi(u)可导\\
&则函数y=f(\Phi(x))在点x处可导,且\frac{dy}{dx}=\frac{dy}{du}.\frac{du}{dx}\\
&或写成[f(\Phi(x))]'=f(\Phi(x))\Phi'(x)\\
\end{align}
\]
例题
\[\begin{align}
&设u=\tan y,x=e^t,试将下面y关于x的函数方程F(\frac{d^2y}{dx^2},\frac{dy}{dx},y,x)=0\\
&解：\\
&y=y(u(t(x))),t=\ln x,y=\arctan u,y=\arctan u(\ln(x))\\
&\frac{dy}{dx}=\frac{dy}{du}*\frac{du}{dt}*\frac{dt}{dx}=\frac{1}{1+u^2}*\frac{du}{dt}*\frac{1}{x}\\
&\frac{d^2y}{dx^2}=d[\frac{dy}{du}]*\frac{du}{dt}*\frac{dt}{dx}+\frac{dy}{du}*d[\frac{du}{dt}]*\frac{dt}{dx}+\frac{dy}{du}*\frac{du}{dt}*d[\frac{dt}{dx}]\\
&[\frac{2u}{(1+u^2)^2}]*\frac{du}{dt}*\frac{dt}{dx}+\frac{1}{1+u^2}*[\frac{d^2u}{dt^2}*\frac{1}{x}]*\frac{1}{x}+\frac{1}{1+u^2}*\frac{du}{dt}*[-\frac{1}{x^2}]\\
&\\
\end{align}
\]
2.隐函数微分法
例题
\[\begin{align}
&设y=y(x)由方程e^y+6xy+x^2-1=0确定,y''(0);设y=y(x)由方程xe^{f(y)}=e^y确定,f二阶可导,且f'\neq1,求y''(x)\\
&e^y*y'+6y+6xy'+2x=0\\
&e^y*y''+e^y*(y')^2+6xy''+12y'+2=0\\
\end{align}
\]
例题
1.
\[\begin{align}
&设f'(x_0)=-1,则\lim_{x\rightarrow 0}\frac{x}{f(x_0-2x)-f(x_0-x)}=?\\
&\\
&解1：\\
&I=\lim_{x\rightarrow 0}\frac{1}{(-2)\frac{f(x_0-2x)-f(x_0)}{(-2x)}+\frac{f(x_0-x)-f(x_0)}{-x}}=-1\\
&解2：\\
&因为f'(x_0)=-1,I=\lim_{x\rightarrow 0}\frac{1}{(-1)*\frac{f(x_0-2x)-f(x_0-x)}{-x}}=-1\\
\end{align}
\]
2.
\[\begin{align}
&设函数f(x)在x=0处连续,且\lim_{h\rightarrow0}\frac{f(h^2)}{h^2}=1,则\\
&(A)f(0)=0且f_{-}'(0)\exist\\
&(B)f(0)=1且f_{-}'(0)\exist\\
&(C)f(0)=0且f_{+}'(0)\exist\\
&(D)f(0)=1且f_{+}'(0)\exist\\
&\\
&解：\\
&因为f(x)在x=0处连续,\lim_{x\rightarrow 0}f(x)=f(0)\\
&因为\lim_{h\rightarrow0}\frac{f(h^2)}{h^2}=1,h\rightarrow0,h^2=0,h\rightarrow0,f(h^2)=0\\
&\lim_{h\rightarrow0}\frac{f(h^2)}{h^2}\overset{令t=h^2}{=}\lim_{t\rightarrow0^+}\frac{f(t)}{t}=\lim_{t\rightarrow0^+}\frac{f(t)-f(0)}{t-0}=0\Leftrightarrow f_{+}'(0)\exist\\
\end{align}
\]
3.
\[\begin{align}
&设f(x)=|x^3-1|\Phi(x),其中\Phi(x)在x=1处连续,则f(x)在x=1处可导的充要条件为\Phi(1)=?\\
&分析问题：f(x)在x=1处什么条件可导\\
&解：\\
&\lim_{x\rightarrow 1^+}\frac{f(x)-f(1)}{x-1}=\lim_{x\rightarrow 1^+}\frac{(x^3-1)\Phi(x)}{x-1}=\lim_{x\rightarrow 1^+}\frac{(x-1)(x^2+x+1)\Phi(x)}{x-1}=3\Phi(1)\\
&\lim_{x\rightarrow 1^-}\frac{f(x)-f(1)}{x-1}=\lim_{x\rightarrow 1^-}\frac{(x^3-1)\Phi(x)}{x-1}=\lim_{x\rightarrow 1^-}\frac{(x-1)(x^2+x+1)\Phi(x)}{x-1}=-3\Phi(1)\\
&\\
&又因f(x)在x=1处连续,则3\Phi(1)=-3\Phi(1),所以\Phi(1)=0\\
&注解：a^n-b^n=(a-b)(a^{n-1}b^0+a^{n-2}b^1+...+a^0b^{n-1})
\end{align}
\]
4.
\[\begin{align}
&设函数f(x)在x=1处连续,且\lim_{x\rightarrow 1}\frac{f(x)}{x-1}=2,求f'(1).
&解：\\
&\lim_{x \rightarrow 1}f(x)=f(1)\\
&\lim_{x \rightarrow 1}\frac{f(x)}{x-1}(x-1)=0=f(1)\\
&f'(1)=\lim_{x \rightarrow 1}\frac{f(x)-f(1)}{x-1}=2
\end{align}
\]
三、参数方程所确定函数的微分法
\[\begin{align}
&设y=y(x)由参数方程\cases{&x=x(t)\\&y=y(t)\\}所确定，则\\
&\frac{dy}{dx}=\frac{y'(t)}{x'(t)}=\Phi'(\Phi^{-1}(x),(\Phi^{-1})(x)),(\Phi^{-1})(t)=\frac{1}{\Phi^1(t)},\frac{y''(t)x'(t)-y'(t)x''(t)}{[x'(t)]^3}\\
&\\
\end{align}
\]
\[\begin{align}
&设y=y(x)由参数方程\cases{&x=x(t)\\&y=y(t)\\}所确定，则\\
&\frac{dy}{dx}=\frac{\frac{dx}{dt}}{\frac{dy}{dt}}=\frac{x'(t)}{y'(t)}\\
&\frac{d^2y}{dx}=\frac{d(\frac{dy}{dx})}{dx}=\frac{(\frac{x'(t)}{y'(t)})'}{x'(t)}\\
\end{align}
\]
例题：
\[\begin{align}
&y=y(x)由参数方程\begin{cases}&x=\ln (1+t)^2\\&y=t-\arctan t\\\end{cases}求\frac{d^2y}{dx}\\
&\frac{dy}{dx}=\frac{\frac{1+t^2}{1+t^2}-\frac{1}{1+t^2}}{\frac{2t}{1+t^2}}=\frac{t}{2}\\
&\frac{d^2y}{dx}=\frac{\frac{1}{2}}{\frac{1}{t^+1}2t}=\frac{t^2+1}{4t}\\
\end{align}
\]
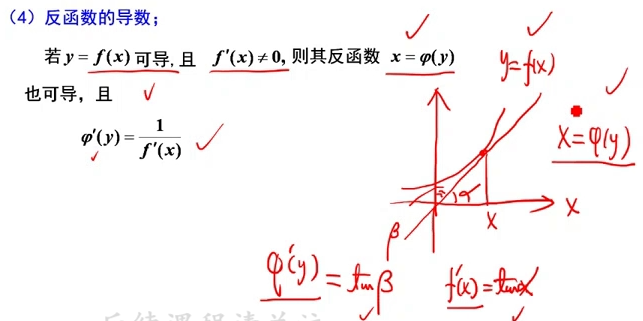
四、反函数的微分法
\[\begin{align}
&设函数y=f(x)二阶可导，且f'(x)\neq0，其反函数是x=f^{-1}(y)\\
&则\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}}=\frac{1}{f'(x)},\frac{d^2x}{dy^2}=-\frac{\frac{d^2y}{dx^2}}{(\frac{dy}{dx})^3}=-\frac{f''(x)}{[f'(x)]^3}
\end{align}
\]
五、分段函数的微分法
在分段区间内，按初等函数的微分法求;在分段点处，用导数、左右导数定义及导数与左右导数的关系求
\[\begin{align}
&设f(x)=\cases{1-2x^2,x\leq -1\\x^3,-1\leq x\leq2\\12x-16,x\geq 2}\\
&(1)求f(x)的反函数g(x)\\
&(2)g(x)是否有间断点、不可导点
\end{align}
\]
