高等数学·不定积分、定积分与反常积分
不定积分、定积分与反常积分
不定积分
一、不定积分概念
1.定义
2.计算
(1)第一换元法(凑微分)
常见凑微分:
(2)第二换元法
1)三角换元
2)倒变换
3)指数(或对数)变换
4)用于有理化的变换
(3)分部积分法
1)降幂法
2)升幂法
3)循环法
4)递推公式法
定积分
一、定积分概念
1.定义
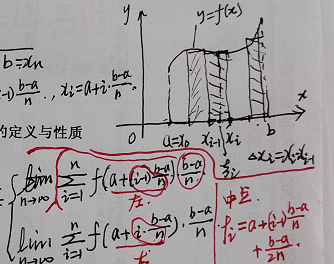
定理:(线性)
注解:积分无小事
2.定积分存在的充分条件
3.定积分的几何意义
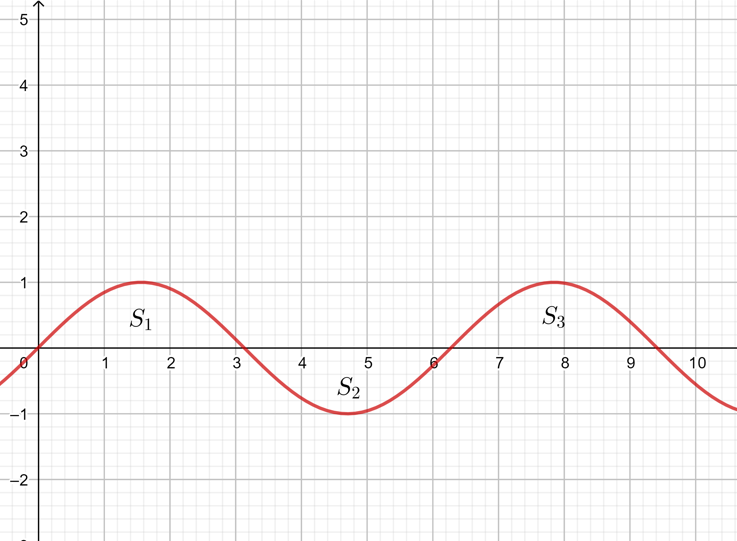
注解:
二、定积分的性质
1.不等式性质
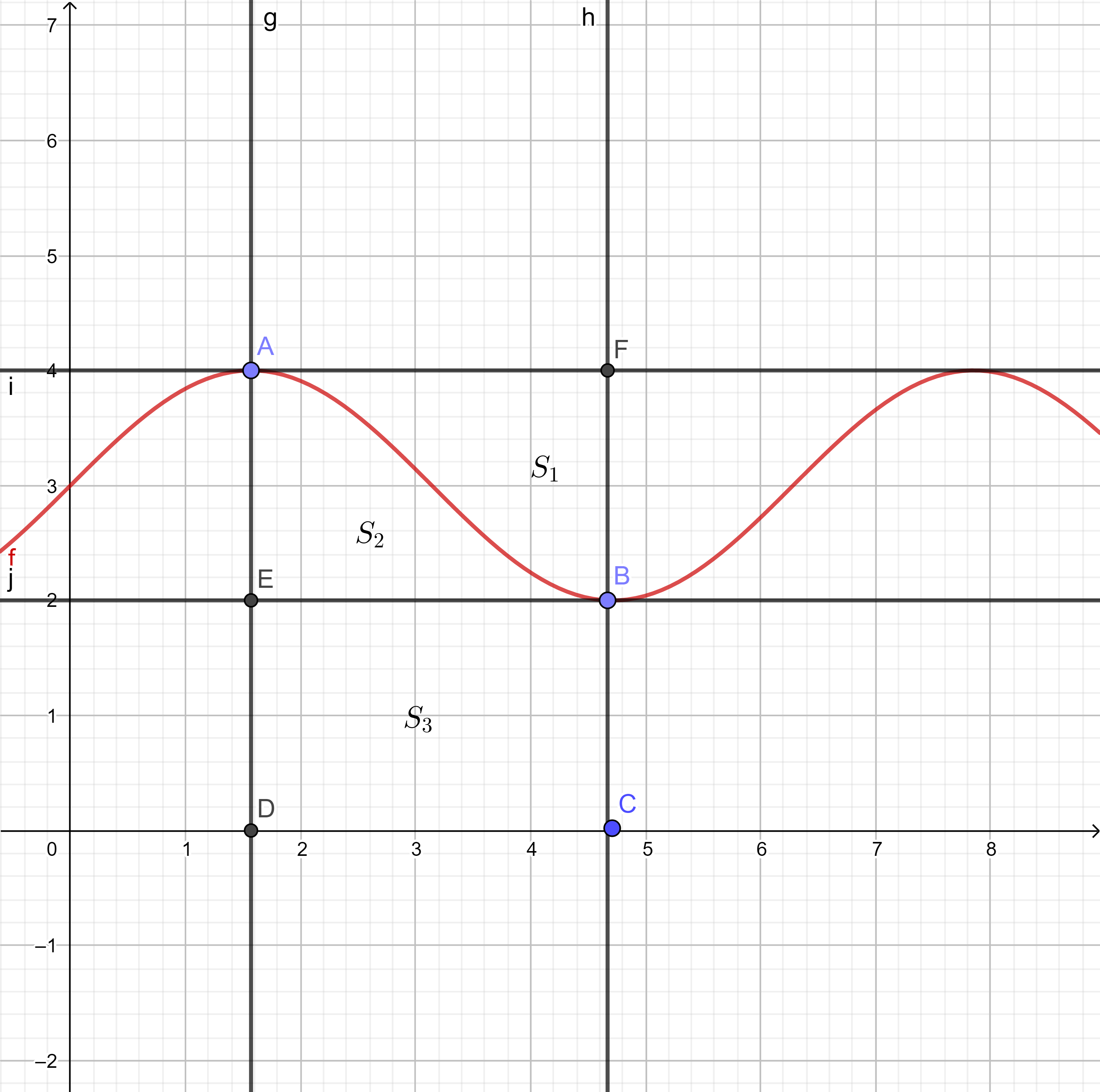
2.中值定理
注解:
例题:
三、积分上限函数
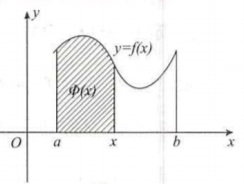
推论:
例题
\begin{align}
&(3)设f(x)连续,\phi(x)=\int_0^1{f(tx)dt},且\lim_{x\rightarrow0}\frac{f(x)}{x}=A(常数),求\phi'(x)并讨论\phi'(x)在x=0处的连续性\
&当x\neq0时\
&令u=tx,t\in[0,1],u=tx\in[0,x],\phi(x)=\int_01f(tx)dt\overset{tx=u}{=}\int_0x{f(u)d(\frac{u}{x})}=\frac{\int_0^xf(u)du}{x}\
&\phi'(x)=\frac{xf(x)-\int_0xf(u)du}{x2}\
&当x=0时,f(0)=0,\phi(0)=f(0)=0,\phi'(0)=\lim_{x\rightarrow0}\frac{\phi(x)\phi(0)}{x-0}=\lim_{x\rightarrow0}\frac{\int_0xf(u)du}{x2}=\lim_{x\rightarrow 0}\frac{f(x)}{2x}=\frac{1}{2}A\
&\lim_{x\rightarrow0}\phi'(x)=\lim_{x\rightarrow 0}{\frac{xf(x)-\int_0xf(u)du}{x2}}=A-\frac{1}{2}A=\frac{1}{2}A=\phi'(0)\Leftrightarrow\phi'(x)在x=0处连续\
\end{align}
\begin{align}
&注意变限积分进行正逆运算时上下限的映射\
&例如F(x)=\int_0x{f(t)dt}\overset{t=-u}{=}\int_{-a}f(-u)d(-u)\
\end{align}
\int_abf(x)dx=F(x)|_ab=F(b)-F(a)
\int_abf(x)dx=\int_\alpha\beta{f(\Phi(t))\Phi'(t)dt}
\int_abudv=uv|_ab-\int_a^bvdu
\begin{align}
&直接使用奇偶性周期性定义证明\
&(1)设f(x)为[-a,a]上的连续函数(a0),则\
&\int_{-a}{a}f(x)dx=
&证:\int_{-a}0{f(x)dx}\overset{x=-t}{=}\int_0a{f(-t)d(-t)}=-\int_{0}{a}f(t)d(t)=-\int_0a{f(x)dx}\
\end{align}
\begin{align}
&(2)设f(x)是以T为周期的连续函数,则对\forall A,有\int_a{a+T}f(x)=\int_0T{f(x)dx}\
&\int_a{a+T}f(x)dx\overset{x=a+t}{=}\int_0T{f(a+t)d(a+t)}=\int_0^{a+t}f(a+t)dt\
\end{align}
\begin{align}
&1.设M=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}{\frac{\sin x}{1+x2}\cos4xdx},N=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}{(\sin x3+\cos4x)dx},P=\int_{-\frac{\pi}{2}}{\frac{\pi}{2}}(x2\sin3x-\cos4x)dx,则\
&(A)N<P<M(B)M<P<N(C)N<M<P(D)P<M<N\
&根据对称性判断\
&M:f_M(x)为奇函数,F_M(x)为偶函数\
&N:N=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}{(\sin x3+\cos4x)dx}=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin 3xdx+\int_{-\frac{\pi}{2}}{2}}\cos ^4xdx\
&\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin 3xdx=0,\int_{-\frac{\pi}{2}}{2}}\cos ^4xdx\geq 0,\Rightarrow N\geq 0\
&P:P=\int_{-\frac{\pi}{2}}{\frac{\pi}{2}}(x2\sin3x-\cos4x)dx=\int_{-\frac{\pi}{2}}{\frac{\pi}{2}}x2\sin3xdx-\int_{-\frac{\pi}{2}}{2}}\cos^4xdx\
&\int_{-\frac{\pi}{2}}{\frac{\pi}{2}}x2\sin3xdx=0,\int_{-\frac{\pi}{2}}{2}}\cos^4xdx\geq0,\Rightarrow P\leq0\
&\Leftrightarrow P<M<N,\space\space选(D)\
\end{align}
\begin{align}
&2.设f(x)=\begin{cases}&kx,0\leq x\leq \frac{1}{2}a\&c,\frac{1}{2}a<x\leq a\end{cases},求F(x)=\int_0^xf(t)dt,x\in[0,a]\
&F(x)=\begin{cases}&\int_0xktdt=\frac{1}{2}kt2|_0x=\frac{1}{2}kx2,0\leq x\leq \frac{1}{2}a\&\int_0{\frac{1}{2}a}ktdt+\int_{\frac{1}{2}a}c cdt=\frac{1}{8}ka2+c2-\frac{1}{2}ac,\frac{1}{2}a<x\leq a\end{cases}\
\end{align}
\begin{align}
&(1)\int_0{\frac{\pi}{2}}{\sinnxdx=\int_0{\frac{\pi}{2}}\cosn xdx=\begin{cases}\frac{n-1}{n}\frac{n-3}{n-2}...\frac{1}{2}\frac{\pi}{2},&n为偶数\frac{n-1}{n}\frac{n-3}{n-2}...*\frac{2}{3},&n为大于1的奇数\end{cases}}\
&(2)\int_0^{\pi}xf(\sin x)dx=\frac{\pi}{2}\int_0^{\pi}f(\sin x)dx(f(x)为连续函数)\
\end{align}
\begin{align}
&\lim_{n\rightarrow \infty}{(\frac{1}{n+1}+\frac{1}{n+2}+...+\frac{1}{n+n})}\
&法1:夹逼定理+基本不等式\
&\frac{1}{1+x}<\ln(x+1)<x\
&令x=\frac{1}{n}\
&得\frac{1}{n+1}=\frac{\frac{1}{n}}{\frac{1}{n}+1}<\ln(\frac{1}{n}+1)=\ln(n+1)-\ln(n)<\frac{1}{n}\
&得\frac{1}{n+2}<ln(n+2)-ln(n+1)<\frac{1}{n+1}\
&得\frac{1}{n+n}<\ln(n+n)-\ln(n+n-1)<\frac{1}{n+n-1}\
&得\frac{1}{n+1}+\frac{1}{n+2}+...+\frac{1}{n+n}<ln(2n)-ln(n)=ln2\
&法2:\lim_{n\rightarrow \infty}{(\frac{1}{n+1}+\frac{1}{n+2}+...+\frac{1}{n+n})}中\
&\frac{1}{n+1}中n为主体,1为变体\
&\frac{变体}{主体}\rightarrow^{n \rightarrow{\infty}}
&\lim_{\lambda \rightarrow 0}{\sum_{i=1}^{n}{f(\xi_i)\Delta x_i}=\lim_{n\rightarrow \infty}\frac{1}{n}\sum_{i=1}{n}f(\xi_i)(b-a)}=\int_01\frac{1}{1+x}=\ln(1+x)|_{0}^{1}=\ln2\
\end{align}
\begin{align}
&设f(x)=\int_0^{\pi}{\frac{\sin x}{\pi-t}dt},计算\int_0^{\pi}f(x)dx.\
&法1:分部积分+换元法\
&原式=xf(x)|_0{\pi}-\int_0dx}\
&=\pi{\int_0{\pi}{\frac{\sin{t}}{\pi-t}dt}-\int_0{\pi-x}}dx}\
&=\int_0^{\pi}{\frac{(\pi-x)\sin x}{\pi-x}dx}=2\
&法2:\
&原式=\int_0\pi{f(x)d(x-{\pi})}=(x-\pi)f(x)|_0-\int_0^{\pi}{\frac{(x-\pi)\sin x}{\pi-x}dx}=2\
&法3:二重积分转化为累次积分\
&原式=\int_0{\pi}{\int_0\frac{x\sin t}{\pi-t}dt}dx\
\end{align}
\begin{align}
&因为\lim_{x\rightarrow 0}{\frac{ax-\sin x}{\int_bx{\frac{\ln{1+t3}}{t}dt}}}=c(c\neq 0)\
&所以\lim_{x\rightarrow 0}{ax-\sin x}=0并且\lim_{x \rightarrow 0}{\int_bx{\frac{\ln{1+t3}}{t}dt}}=0\
&化简,使用洛必达法则上下求导\
&\lim_{x\rightarrow 0}{\frac{ax-\sin x}{\int_bx{\frac{\ln{1+t3}}{t}dt}}}=\lim_{x\rightarrow 0}{\frac{a-\cos x}{\frac{\ln{1+x^3}}{x}}}=\lim_{x\rightarrow 0}{\frac{a-\cos x}{x^2}}\
&\Rightarrow a=1,c=\frac{1}{2},b=0\
\end{align}
\begin{align}
&(1)\int_a^{+\infty}{f(x)}dx=\lim_{t\rightarrow +\infty}{\int_{a}^{t}f(x)dx}\
&(2)\int_{-\infty}^{b}{f(x)}dx=\lim_{t\rightarrow -\infty}{\int_{t}^{b}f(x)dx}\
&(3)\int_{-\infty}{0}{f(x)}dx和{\int_{0}f(x)dx}都收敛,则{\int_{-\infty}^{+\infty}f(x)dx}收敛\
&且{\int_{-\infty}{+\infty}f(x)dx}=\int_{-\infty}dx+{\int_{0}^{+\infty}f(x)dx}\
&如果其中一个发散,结果也发散\
&常用结论:\int_a{+\infty}{\frac{1}{xp}dx}\begin{cases}&p1,收敛\&p\leq1 ,发散\end{cases},(a0)\
\end{align}
\begin{align}
&如果函数f(x)在点a的任一领域内都无界,那么点a为函数f(x)的瑕点(也称为无界点).无界函数的反常积分也成为瑕积分\
&(1)设函数f(x)在(a,b]上连续,点a为f(x)的瑕点.如果极限\lim_{t\rightarrow a+}{\int_{t}{f(x)dx}}\exist,\
&则称此极限为函数f(x)在区间[a,b]上的反常区间,记作\int_{a}{b}f(x)dx,即\int_{a}f(x)dx=\lim_{t\rightarrow a+}{\int_{t}{f(x)dx}}\
&这时也称反常积分\int_ab{f(x)dx}收敛,如果上述极限不存在,则反常积分\int_ab{f(x)dx}发散\
&(2)设函数f(x)在[a,b)上连续,点b为函数f(x)的瑕点,则可以类似定义函数f(x)在区间[a,b]上的反常积分\int_a^bf(x)dx=\lim_{t\rightarrow b-}{\int_atf(x)dx}\
&设函数f(x)在[a,b]上除点c(a<c<b)外连续,点c为函数f(x)的瑕点,如果反常积分\int_ac{f(x)dx}和\int_cb{f(x)dx}都收敛\
&则称反常积分\int_ab{f(x)dx}收敛,且\int_ab{f(x)dx}=\int_ac{f(x)dx}+\int_cb{f(x)dx}\
&如果至少一个发散,则称\int_a^b{f(x)dx}发散\
&常用结论:\
&\int_ab{\frac{1}{(x-a)p}}\begin{cases}&p<1,收敛\&p\geq 1,发散\end{cases}\
&\int_ab{\frac{1}{(x-a)p}}\begin{cases}&p<1,收敛\&p\geq 1,发散\end{cases}\
\end{align}
\begin{align}
&(1)若平面域D由曲线y=f(x),y=g(x)(f(x)\geq g(x)),x=a,x=b(a<b)所围成,则平面域D的面积为\
&S=\int_a^b{[f(x)-g(x)]dx}\
&(2)若平面域D由曲线由\rho=\rho(\theta),\theta=\alpha,\theta=\beta(\alpha<\beta)所围成,则其面积为S=\frac{1}{2}\int_{\alpha}{\beta}{\rho2(\theta)d\theta}
\end{align}
\begin{align}
&若区域D由曲线y=f(x)(f(x)\geq 0)和直线x=a,x=b(0\leq a<b)及x轴所围成,则\
&(1)区域D绕x轴旋转一周所得到的旋转体体积为V_x=\pi\int_ab{f2(x)dx}\
&(2)区域D绕y轴旋转一周所得到的旋转体体积为V_y=2\pi\int_a^b{xf(x)dx}\
&(3)区域D绕y=kx+b轴旋转一周所得到的旋转体体积为V=2\pi\int_D\int{r(x,y)d\sigma}\
&例如:求y=x,y=x^2在第一象限的封闭图形绕转轴的体积\
\end{align}
\begin{align}
&V_x=2\pi\int_D\int yd\sigma=2\pi\int_01{dx}\int_{x2}^{x}ydy\
&V_y=2\pi\int_D\int xd\sigma=2\pi\int_01{dx}\int_{x2}^{x}xdy\
&V_{x=1}=2\pi\int_D\int (1-x)d\sigma\
&V_{y=2}=2\pi\int_D\int (2-y)d\sigma\
\end{align}
\begin{align}
&(1)C:y=y(x),a\leq x\leq b,s=\int_ab{\sqrt{1+y'2}dx}\
&(2)C:\begin{cases}&x=x(t)\&y=y(t)\end{cases},\alpha \leq t\leq \beta,s=\int_{\alpha}{\beta}{\sqrt{x'2+y'^2}dx}\
&(3)C:\rho=\rho(\theta),\alpha \leq \theta\leq \beta,s=\int_{\alpha}{\beta}{\sqrt{\rho2+\rho'^2}dx}\
\end{align}
\begin{align}
&曲线y=f(x)(f(x)\geq 0)和直线x=a,x=b(0\leq a<b)及x轴所围成的区域绕x轴旋转所得到的旋转体的侧面积为\
&S=2\pi\int_ab{f(x)\sqrt{1+f'2(x)}dx}\
\end{align}
\begin{align}
&分析题意可知,该容器由x2+y2=1的圆和x2+(y-1)2=1的偏心圆组成\
&根据图像的对称性可以避免不同表达式带来的困难\
&对圆的小带子进行积分,带子长度为x,积分区间为-1到\frac{1}{2},\int_{-1}^{\frac{1}{2}}{\pi x^2dy}\
&由于图像的对称性,将积分结果乘二\
&(1)V=2\pi\int_{-1}{\frac{1}{2}}{x2}dy=2\pi\int_{-1}{\frac{1}{2}}{(1-y2)dy}=\frac{9\pi}{4}\
\end{align}
\begin{align}
&(2)W=FS=GS=mgS=\rho VSg\
&上部为W_1=\int_{\frac{1}{2}}{2}(2y-y2)(2-y)dy\rho g\
&下部为W_2=\int{\frac{1}{2}}_{-1}(1-y2)(2-y)dy*\rho g\
&W=W_1+W_2\
\end{align}
\begin{align}
&F_p=PA=\rho ghA\
&将图像分为上部和下部,上部为矩形区域和下部的抛物线围成的面积区域,对其进行依次求解\
&P_1=2\rho gh\int_1^{h+1}{h+1-y}dy=\rho gh^2\
&P_2=2\rho gh\int_0^1{(h+1-y)\sqrt{y}dy=4\rho g(\frac{1}{3}h+\frac{2}{15})}\
&\frac{P_1}{P_2}=\frac{4}{5}\Rightarrow h=2,h=-\frac{1}{3}(舍去)
\end{align}





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!